Задача 5. Решение системы линейных алгебраических уравнений методом итераций (метод зейделя)

Пусть требуется найти решение систем линейных алгебраических уравнений:

(4.23)

с заданной точностью >0.

Предположим, что все диагональные коэффициенты и перепишем систему в следующем виде:

(4.24)

Возьмем некоторое начальное приближение к решению системы и подставим в правые части системы (4.24). Полученные значения

являются первым приближением.

Так, на м шаге будем иметь:

(4.25)

Описанный метод носит название метода простой итерации.

Итерационный процесс будет сходящимся, т.е. решение 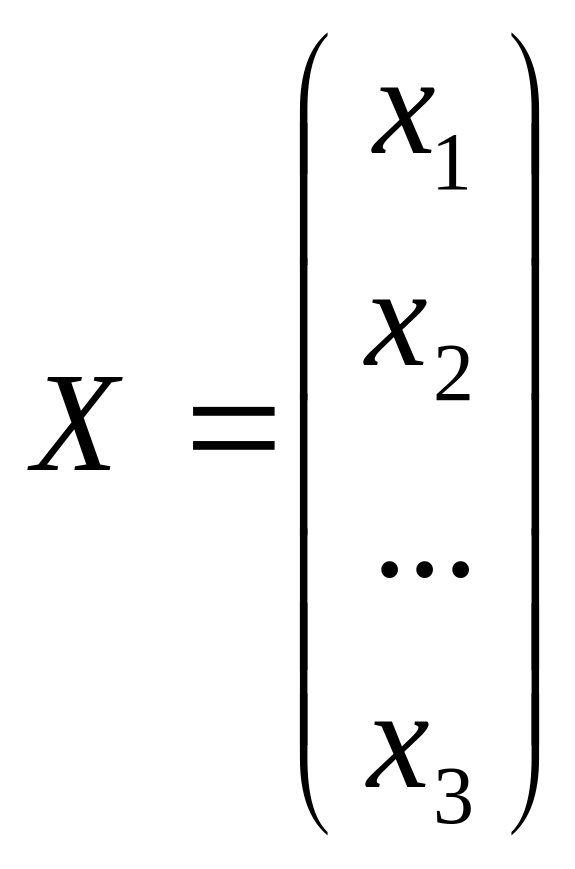удовлетворяет соотношению или

если выполняется неравенство

(4.26)

Итерационный процесс продолжается до тех пор, пока все не станут близки к . Критерий близости можно задать в форме

 при >0.

Метод Зейделя отличается от изложенного метода простой итерации тем, что при вычислении используются уже найденные на ом шаге значения , т.е. если то

где .

Пример.

Решить систему линейных уравнений методом Зейделя

 =0,0001

Решение.

Приведем систему к виду (2):

Нулевое приближение

Используя формулу итерационного процесса Зейделя, приведем систему к виду:

Получим приближение

Затем проведем последующие вычисления, сведя результаты в таблицу 4.2:

Таблица 4.2

Итерации	Х1	Х2	Х3
0	0	0	0
1	0.1000Е+01	0.1333Е+01	0.1133Е+01
2	0.1050Е+01	0.9473 Е+00	0.9889 Е+00
3	0.9896 Е+00	0.1005 Е+01	0.9999 Е+00
4	0.1001 Е+01	0.9999 Е+00	0.1000 Е+01
5	0.1000 Е+01	0.1000 Е+01	0.1000 Е+00

Как видно из таблицы, требуемая точность достигнута уже на пятом шаге. Это показывает, что метод Зейделя сходится довольно быстро.

Задача 6. Решение системы линейных алгебраических уравнений методом гаусса

Рассмотрим один из наиболее известных и широко применяемых прямых методов решения систем линейных уравнений. Обычно этот метод называют методом исключения или методом Гаусса.

Чтобы проиллюстрировать этот метод, рассмотрим сначала систему из трех уравнений с тремя неизвестными:

(4.27)

В такой системе по крайней мере один из коэффициентов , , должен быть отличен от нуля, иначе бы мы имели бы дело в этих трех уравнениях только с двумя неизвестными. Если , то можно переставить уравнения так, чтобы коэффициент при в первом уравнении был отличен от нуля. Очевидно, что перестановка уравнений оставляет систему неизменной: ее решение остается прежним.

Теперь введем множитель .

Умножим первое уравнение системы (4.27) на и вычтем его из второго уравнения системы. («Первое» и «второе» уравнения берем уже после перестановки, если она была необходима). Результат вычитания равен:

Так как

,

фактически исключается из второго уравнения (именно для достижения такого результата и было выбрано значение ).

Определим теперь новые коэффициенты

.

Тогда второе уравнение системы приобретает вид

(4.28)

Заменим второе из первоначальных уравнений уравнением (4.28) и введем множитель для третьего уравнения

.

Умножим первое уравнение на этот множитель и вычтем его из третьего. Коэффициент при снова становится нулевым, и третье уравнение приобретает вид

(4.29)

где

.

Если теперь в исходной системе уравнений (4.27) заменить третье уравнение на (4.29), то новая система выглядит так:

(4.30)

Эти новые уравнения полностью эквивалентны исходным уравнениям с тем преимуществом, что входит только в первое уравнение и не входит ни во второе, ни в третье. Таким образом, два последних уравнения представляют собой систему из двух уравнений с двумя неизвестными; если теперь найти решение этой системы, т.е. определить и , то результат можно подставить в первое уравнение и найти . Иначе говоря, задача сведена к решению системы из двух уравнений с двумя неизвестными.

Попытаемся теперь исключить из двух последних уравнений. Если , то снова мы переставим уравнения так, чтобы было отлично от нуля (если и , то система вырождена и либо вовсе не имеет решения, либо имеет бесчисленное множество решений).

Введем новый множитель

.

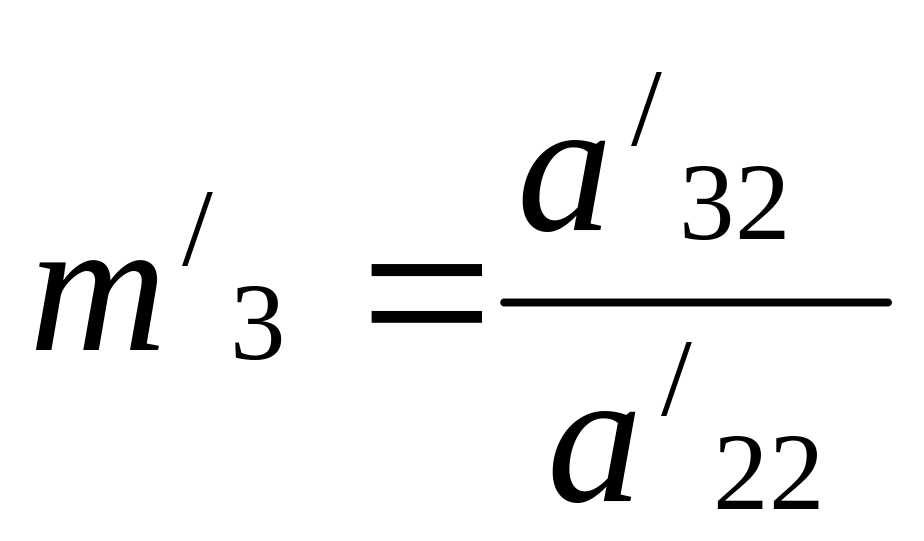Умножим второе уравнение полученной системы (4.30) на и вычтем его из третьего. Результат вычитания равен

В силу выбора

.

Полагая, что

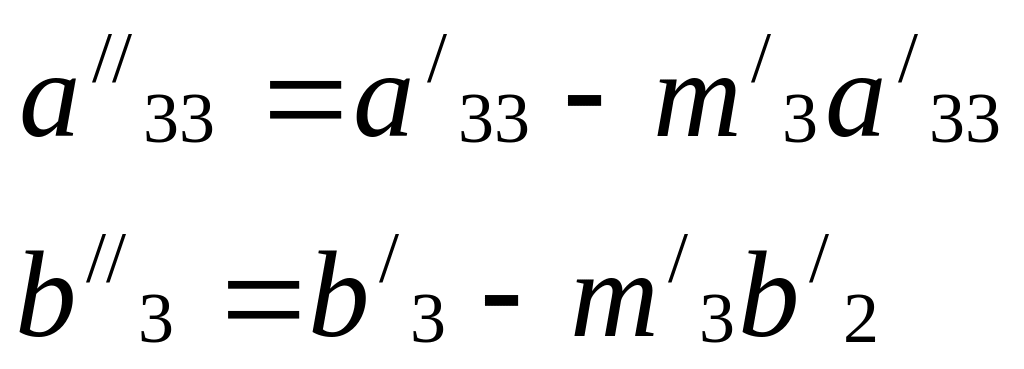
окончательно получим

(4.31)

Третье уравнение полученной системы (4.30) можно заменить уравнением (4.31), после чего система уравнений приобретает следующий вид:

(4.32)

Такая система уравнений (4.32) иногда называется треугольной из-за своего внешнего вида.

Для решения необходимо определить из третьего уравнения системы (4.32), подставить этот результат во второе уравнение и определить . Полученные значения и подставить в первое уравнение и определить . Этот процесс, который обычно называется обратной подстановкой (обратный ход), определяется формулами:

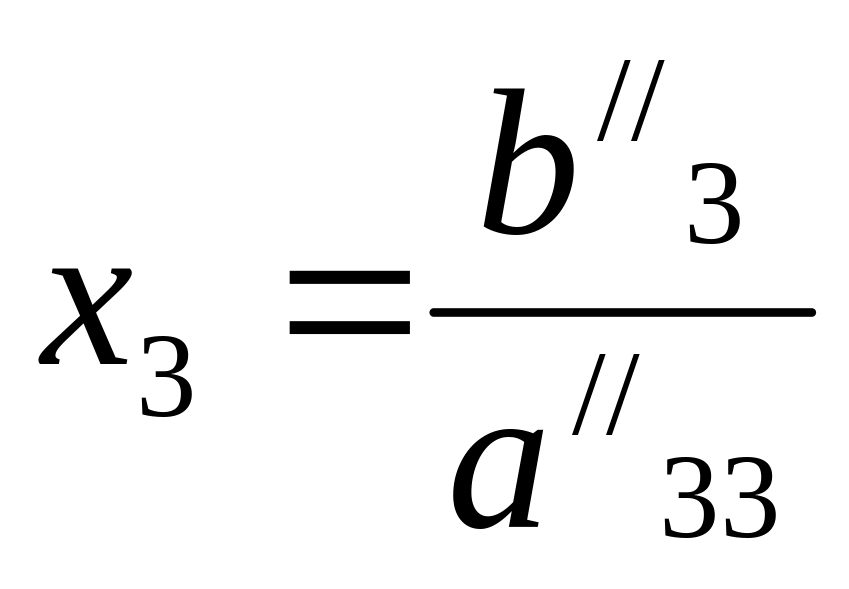
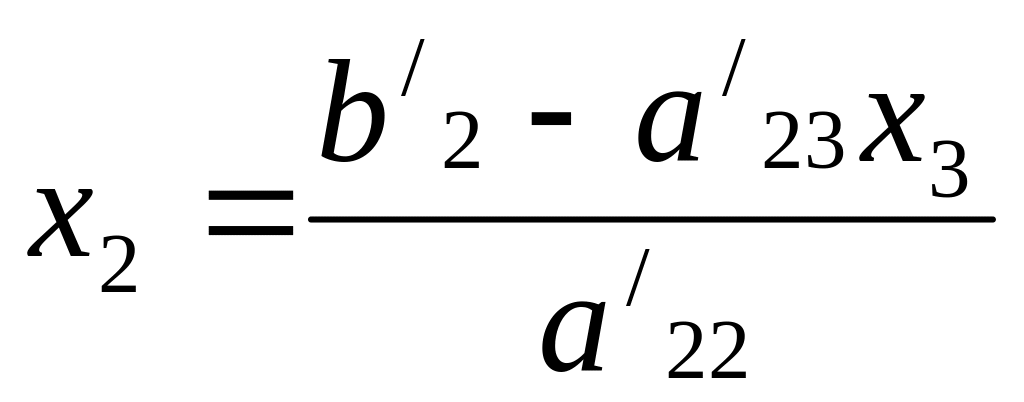(4.33)

.

Необходимо отметить, если , то система уравнений вырождена.

Пример.

Дана система уравнений:

Найти решение системы уравнений.

Решение.

Легко убедиться, что множители для второго и третьего уравнений равны 2 и 1. После исключения из второго и из третьего уравнений, новый множитель, исключающий из третьего уравнения, равен –2. Треугольная система уравнений имеет вид

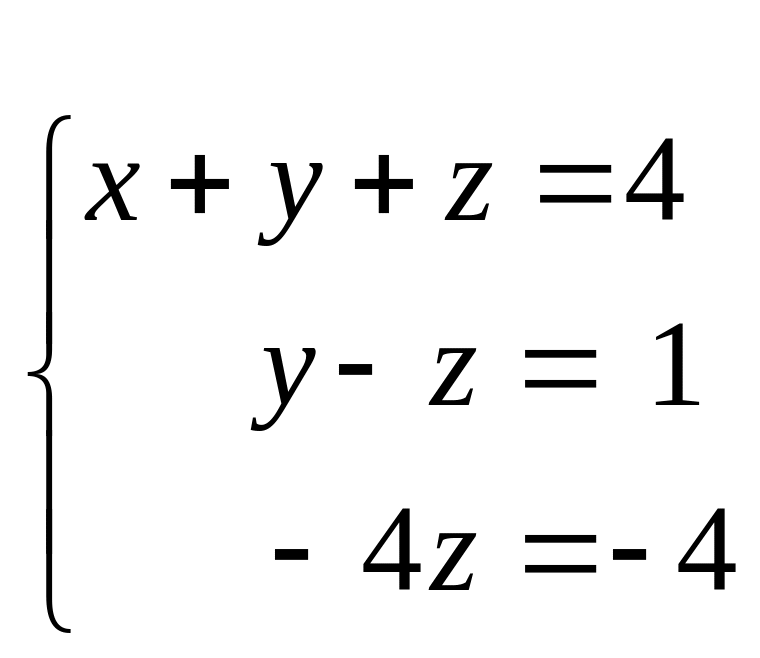
Из последнего уравнения , из второго , из первого . Можно подставить эти значения в исходные уравнения и убедиться, что они точно удовлетворяютcя.

Теперь можно обобщить этот метод на случай системы из n – уравнений с n-неизвестными. Ниже записана система уравнений, приведенная к треугольному виду (4.34).

(4.34)

Формулы для вычисления неизвестных (обратный ход) будут иметь вид:

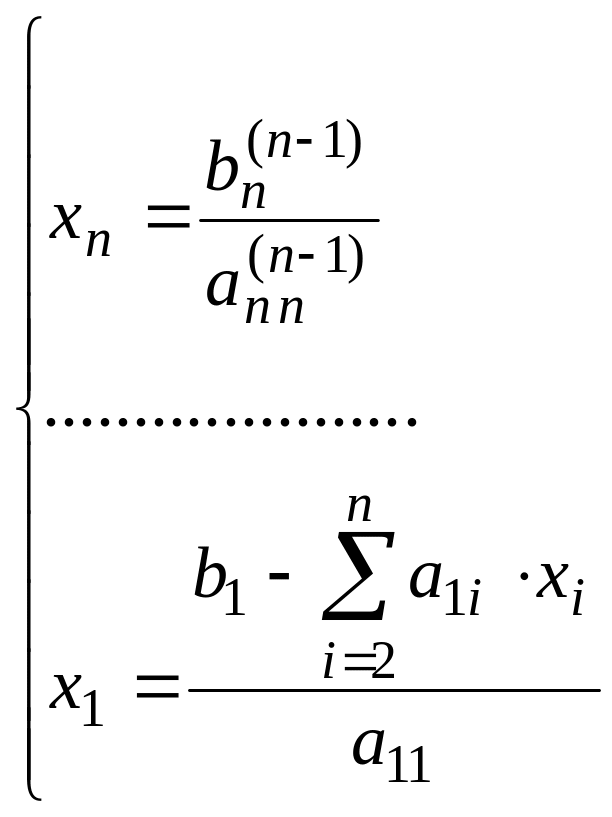(4.35)