12. Число е.

ТЕОР2: Рассмотрим последовательность Xn= и докажем, что эта последовательность сходящаяся и ее предел равен е.

Док-во: Докажем, что она сходится. Для этого достаточно доказать, что она возрастающая и ограниченная сверху.

1. Докажем, что последовательность {Xn} возрастающая, т. е. для n Xn<Xn+1.

(1+1/n) разложим по формуле бинома Ньютона.

Xn = (1+1/n) = 1+(n/1!) (1/n)+(n (n – 1)/2!) (1/n )+(n (n – 1) (n – 2)/3!) (1/n )+K+(n (n – 1) (n – 2)) K(n – (n – 1))/n!) (1/n ) = 2+(1/2!) (1 – 1/n)+(1/3!) (1 – 1/n) (1 – 2/n)+K+(1/n!) (1 – 1/n) (1 – 2/n) K(1 – (n – 1)/n)

Аналогично для Xn+1. Для любого 0<k<n выполняется соотношение (1 – 1/k)<(1 – 1/(k+1)).  Ввыражении для Xn+1 каждое слагаемое больше, чем соответствующее слагаемое в выражении для Xn.  Xn< Xn+1 для любого n.  {Xn} – возрастающая последовательность.

2. Докажем, что последовательность {Xn} – ограничена сверху. Рассмотрим выражение для Xn. Так как 1/k!<1/2 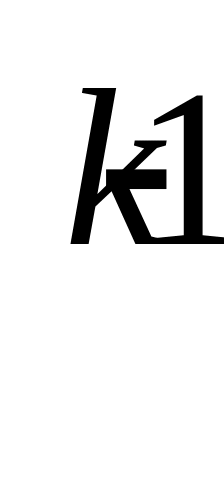при k>2, то Xn<2+1/2!+1/3!+…+1/n!<1+1+1/2+1/4+1/8+…+1/2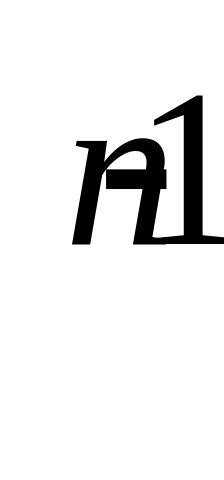 =1+(1 – 1/2 )/(1 – 1/2) = 1+2(1 – 1/2 ) = 3 – 1/2 <3.  Для n 2<Xn<3 и последовательность {Xn} ограничена сверху. По Т о мон огр последовательности она является сходящейся. Ее предел на бесконечности Эйлер обозначил через е.

ОПР1: Число е – иррациональное, это число не может быть корнем никакого алгебраического уравнения с целыми коэффициентами. Такие иррациональные числа называются трансцендентными.

12. Теорема о вложенных промежутках.

ТЕОР1: Для любой последовательности вложенных отрезков существует единственная точка, принадлежащая всем этим отрезкам.

12. Понятие функции и способы ее задания.

ОПР1: Если для любого элемента хХ поставлен в соответствие по закону f единственный элемент уУ, то на множестве Х задана функция y=f (x), причем х – независимая переменная (аргумент), все значения х – область определения функции D (f); совокупность всех значений функции f (x) – область значений функции Е(f).

ОПР2: Функцию, D(f) и E(f) которой являются числовые множества, называют числовой функцией одной действительной переменной.

ОПР3: Графиком функции f(x) является множество точек плоскости, абсцисса которых равна аргументу, а ордината равна значению функции.

ОПР4: Графиком числовой функции f, заданной на числовом промежутке Х, называется множество G всех точек координатной плоскости, имеющих вид М(х; f(х)), где хХ, т.е. {(х; у): у=f(х); хХ}.

ОПР5: Функция задана аналитически, если закон, устанавливающий соответствие между множествами всех значений аргумента и функции, задается формулой.

Преимущества: сжатость, компактность задания, можно вычислить значение функции для любого значения аргумента из области определения, можно применить к данной функции аппарат мат анализа.

ОПР6: Табличный способ задания заключается в задании таблицы определенных значений аргумента и соответствующих им значений функции.

ОПР7: При графическом способе задания функции соответствие между аргументом и функцией задается посредствам графика.

Преимущества: наглядность, что делает его чрезвычайно полезным при изучении функции.

ОПР8: Пусть заданы две функции y = f(x) и z = F(y), при чем D(F)E(f), тогда для любого хХ соответствует zZ, где z = F(y), y = f(x), значит z=F(f(x)). Эта функция, определяемая соответствием называется сложной функцией или суперпозицией функций f и F.

ОПР10: Всякая функция, которая задана явным образом с помощью формулы, содержащей конечное число арифметических операций и суперпозиций элементарных функций называется элементарной функцией. D(f) = R для основных элементарных функций, при которых данная функция имеет смысл; E(f) - тоже вещественные числа.

ОПР9: Классификация функций. Это основные элементарные функции.

1. Степенная: у = .

2. Показательная: у = .

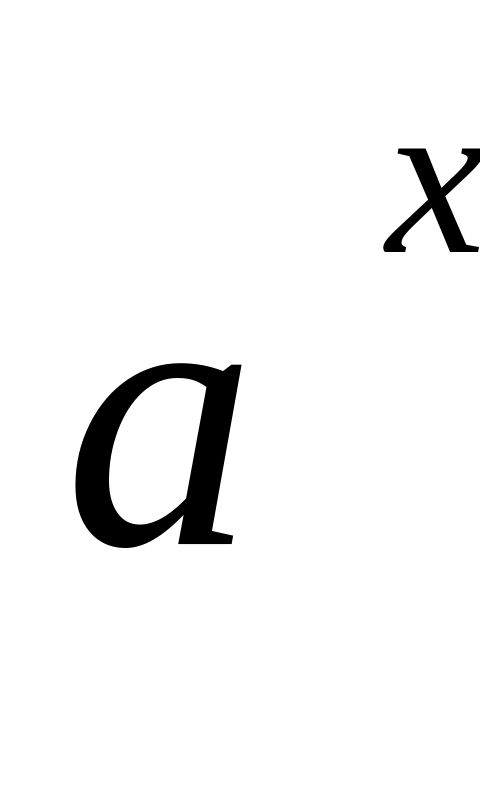3. Логарифмическая: у = 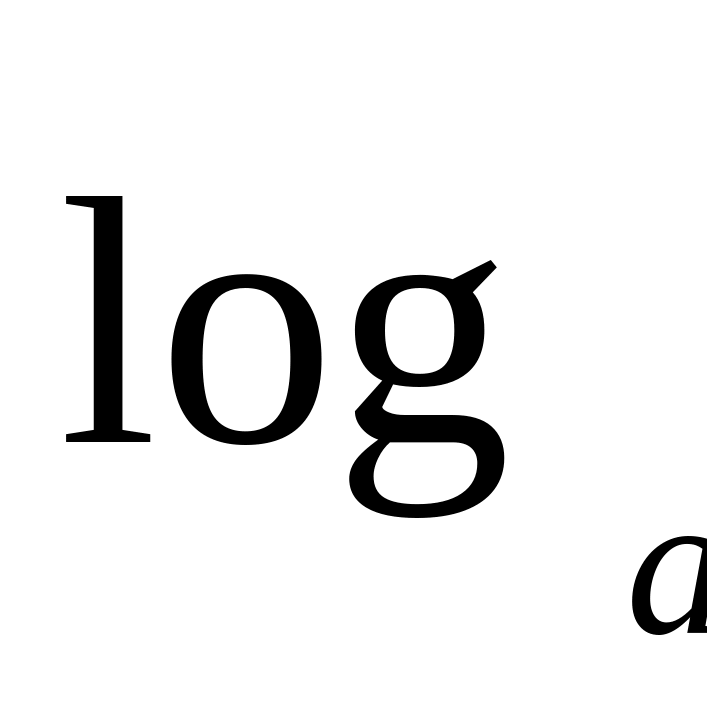x.

4. Тригонометрические.

5. Обратные тригонометрическим.

6. y = const.

1)Многочлены (полиномы): Р(Х)=А0+А1*Х+А2* + …+Аn*

2)Рациональные R(x) = , P(x) и Q(x) – многочлены.

3) Алгебраические, которые заданы с помощью суперпозиции рациональных функций, степенных с иррациональным показателем и арифметических действий.

4) Трансцендентные –элементарные функции, которые не являются алгебраическими. Все тригонометрические, обратные им, показательная, логарифмическая.