16.Связь между f(X) и f(X) для непрерывной св.

Пусть с испытанием связана непрерывная СВ xс плотность вероятности f(x) и функцией распределения F(x). Справедливы равенства:

1. F(x)=

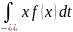
2. f(x)= F’(x)

Док-во:

1. F(x)= 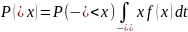по свойству плотности вероятности

2. = =F’(x),

Вопрос 32: теорема Бернулли.

Вероятность случайного события есть доля наступления этого события в длинной серии независимых одинаковых испытаний. Укажем строгую математическую формулировку этого утверждения.

Пусть выполняется серия n независимых одинаковых испытаний и при каждом испытании событие А наступает с вероятностью р. Обозначим W_n= число наступлений события А/ n.

Число W_n называется частотой события А в серии из n испытаний.

Теорема. В указанной ситуации при неограниченном возрастании числа независимых испытаний частота случайного событий А сходится по вероятности к вероятности этого события: W_n → p при n → ∞

Доказательство. Очевидно, W_n – случайная величина, при этом справедливо равенство.

W_n= ξ1+ ξ₂+…+ ξ_n/n, где ξ_i – число наступлений события А в i-ом испытании.

Проверим, что случайные величины ξ_i удовлетворяют условиям теоремы Чебышева.

ξ1, ξ2, …, ξn независимы в силу независимости испытаний.

Закон распределения случайной величины ξi для всех i=1, .., n имеет вид ξi =

= (0 1), q=1-p (34)

(q p)

Отсюда M[ξ_i] = p*1+0*q=p, D[ξ_i] = p(1-p)² + q(0-p)²=pq. (35)

Следовательно, случайные величины ξi однотипны с числовыми характеристиками: a=p, D=pq.

В силу теоремы Чебышева среднее арифметическое этих случайных величин сходится по вероятности к их общему математическому ожиданию:

ξ1+ ξ₂+…..+ ξn / n → р при n→ ∞, что и требовалось.

Замечание 1: Из сказанного выше следует: число успехов(наступлений события А в схеме Бернулли) дается формулой ξ= ξ1+ ξ2+….+ ξ_n,

Где ξ_i-число успехов в i-ом испытании.

Из всего этого следует: М[ξ]=n p, D[ξ]=npq.(37)

Таким образом, числовые характеристики биномиальной случайной величины с параметрами(n,p) даются формулами (37).

Замечание 2:Индикатором связанного с испытанием события А называется случайная величина, равная 1, если событие А произойдет и 0, если событие А не произойдет. Очевидно, закон распределения индикатора имеет вид (34), где р – вероятность наступления, q- вероятность ненаступления события А.

Вопрос 33:Центральная предельная теорема.

При изучении нормального распределения было сформулировано следующее утверждение: если случайные величины ξ1, ξ2,…, ξn зависимы и нормальны с одними и теми же (а, σ), то сумма ξ1+ ξ2+….+ ξ_n также нормальна. Оказывается справедливо гораздо более глубокое утверждение: если случайные величины независимы и имеют один и тот же закон распределения (неважно какой), то при достаточно большом числе слагаемых сумма ξ1+ ξ2+….+ ξ_n приближенно нормальна. Это утверждение называется центральной предельной теоремой теории вероятности.

Приведем строгую формулировку этой теоремы.

Рассмотрим бесконечную последовательность независимых случайных величин ξ1, ξ2,…, ξn, ….. с одним и тем же законом распределения, в частности, с одними и теми же параметрами (а, σ).

Сумма первых n случайных величин ξ1+ ξ2+….+ ξ_n (38) имеет числовые характеристики M=na, D=nσ2 ---- СКО= σ√n (39)

Обозначим Fn(x) функцию распределения случайной величины (38). Поставим вопрос: КАК МЕНЯЕТСЯ Fn(x) при неограниченном возрастании числа слагаемых?

Функция распределения нормальной случайной величины с числовыми характеристиками (39) имеет вид Фn(x)=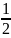 + Ф (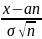 ), где Ф (х) – функция Лапласа. Справедлива теорема. В указанной ситуации имеет место соотношение max|Fn(x)-Фn(x)| →0 при n → ∞.

При достаточно большом числе слагаемых сумма (38) независимых случайных величин с одним и тем же законом распределения с большой точностью подчинена нормальному закону с параметрами (na, σ√n) независимо от закона распределения слагаемых.

Тогда F(x)= + Ф( )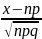

Откуда получаем P(m1< ξ<m2) ≈ Fξ (m2) – Fξ (m1)=Ф( )-Ф(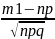 )