
- •1.Классическое определение вероятности
- •2.Геометрическое определение вероятности
- •6 7Б 3ч 4б 6ч 2б 8ч . Формула полной вероятности
- •8.Схема с повторением испытаний (схема Бернулли)
- •12. Числовые характеристики св. Математическое ожидание.
- •49. Интервальные оценки параметров распределения
- •18.Биномиальный закон распределения вероятности
- •19. Равномерный закон распределения случайных величин
- •36.Классификация смо
- •38. Время обслуживания.
- •39. Смо с отказами.
- •22 .Показательный закон
- •40 Система уравнений Эрланга
- •41 Установившийся режим работы смо
- •43 Смо с ограниченной очередью ожидания
- •23.Нормальный закон
- •21.Поток событий
- •13. Дисперсия и ско, свойства
- •14. Плотность вероятности непрерывной св
- •15.Функция распределения случайной величины.
- •16.Связь между f(X) и f(X) для непрерывной св.
- •Вопрос 32: теорема Бернулли.
- •Вопрос 33:Центральная предельная теорема.
- •Вопрос 35: Основные элементы смо.
- •Вопрос 34: Доказательство интегральной формулы Муавра-Лапласа.
6 7Б 3ч 4б 6ч 2б 8ч . Формула полной вероятности
1 2 3
Испытание: из наудачу взятой урны наугад извлекаем шар. Найти: вероятность того, что он белый. Событие А – белый шар. Р(А)-? Введем 3 предположения – гипотезы(Н): Н1 – шар извлекается из 1 урны; Н2 – из 2 урны; Н3 – из 3 урны. Р(Н1) = Р(Н2) = Р(Н3) = 1/3 – гипотезы являются равновозможными. Тогда Р(А) = Р(Н1*А+Н2*А+Н3*А) – события несовместные. Р(А) = Р(Н1*А)+Р(Н2*А)+Р(Н3*А) = Р(Н1)*Р(А/ Н1)+ Р(Н2)*Р(А/ Н2)+ Р(Н3)*Р(А/ Н3) = 1/3*7/10+1/3*4/10+1/3*2/10 = (7+4+2)/30 = 13/30
Отметим, что гипотезы являются несовместными событиями, одно из которых обязательно реализуется в результате испытания. Сумма вероятностей гипотез равна единице. Вложим данный пример в общую схему: пусть интересующее нас событие А может появиться совместно с одной из n взаимноисключающих гипотез. Тогда рассуждая аналогично рассмотренному примеру, используя теоремы сложения и умножения вероятностей получим следующую формулу : Р(А) = Р(Н1)*Р(А/ Н1)+ Р(Н2)*Р(А/ Н2)+…+ Р(Нn)*Р(А/ Нn)
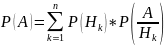
7. Формула Байеса
1
7б
3ч
2б
8ч
2
Из наудачу взятой урны извлекаем шар. Известен результат испытания: событие А – белый шар. Н1 - шар извлекается из 1 урны. Н2 – из 2 урны. В этой ситуации гипотезы Н1 и Н2 не являются равновозможными, т.к. в 1 урне намного больше белых шаров, поэтому вероятность извлечения из 1 урны больше, чем из 2.
Вложим данную задачу в следующую общую схему: пусть интересующее нас событие А может появиться совместно с одной из n взаимноисключающих гипотез Н1, Н2, …, Нn и испытание произвели и известен результат испытания – событие А. Найти вероятности Нk при известном событии А. (Р(Нk/А)-?)
Справедлива
след.формула:
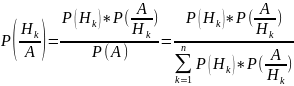 формула Байеса
формула Байеса
Р(Нk*А)= Р(Нk) * Р(А/Нk) и Р(Нk*А)= Р(А)*Р(Нk/А) => Р(Нk) * Р(А/Нk) = Р(А)*Р(Нk/А) =>
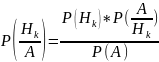
Вернемся
к примеру: Р(Н1/А)
=
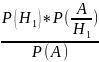 =
=
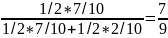
8.Схема с повторением испытаний (схема Бернулли)
Рассмотрим след.часто встречающуюся ситуацию:
1. Проводится n-независимых испытаний. Независимость испытаний означает, что в каждом следующем испытании полностью воспроизводится весь комплекс условий, при которых проводилось предыдущее испытание. 2. Интересующее нас событие А в каждом испытании может появиться с одной и той же вероятностью р и не появиться с вероятностью q=1- p Такая ситуация называется схемой повторения испытаний или схемой Бернулли.
Назовем
событие А успехом и обозначим через
ξ(кси)
– число успехов в серии n-независимых
испытаний. Очевидно кси может принимать
значения 0,1,2, …, n.
Как найти вероятности этих значений?
Р(ξ=k)-?
k=0,1,2…
n
Справедлива формула:
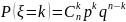
Пример:
бросаем монету 10 раз. Найти вероятность
того, что герб выпадет 3 раза. А –
выпадение герба(успех), ξ-
число успехов = 3, n=10
(число испытаний), р=1/2 (вероятность
успеха), q
= 1-1/2=1/2.
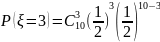
12. Числовые характеристики св. Математическое ожидание.
Пусть
с испытанием связана дискретная СВ
ξ(кси).
Закон распределения имеет вид – ξ:
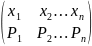 ,
,
Тогда математическим ожиданием СВ ξ(кси) называется сумма произведений значений СВ на их вероятности и обозначается М[ξ] или mξ =х1*Р1+х2*Р2+…+хn*Рn
Мат.ожидание характеризует центральное значение СВ с учетом возможных значений и вероятностей этих значений. Наименее вероятные значения СВ вносят малый вклад в формирование мат.ожидания. Наиболее вероятные значения СВ вносят больший вклад в формирование мат.ожидания.
Св-ва мат.ожиданий:
1) М[a] = a (а – неслучайная величина – const) Мат.ожид.неслучайной величины=самой величине.
2) М[aξ] = a М[ξ] – постоянный множитель можно вынести за знак мат.ожидания.
3) М[ξ+η] = М[ξ]+М[η] мат.ожидание суммы СВ равно сумме мат.ожиданий.
4)М[ξ*η] = М[ξ]*М[η], если ξ и η – статистически независимы
Доказательства:
1)
а:[
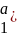 ; ma
= a*1=
a
; ma
= a*1=
a
2) ξ: ; mξ =х1Р1+х2Р2+…+хnРn
аξ:
 ;
mаξ
=ах1Р1+ах2Р2+…+ахnРn
;
mаξ
=ах1Р1+ах2Р2+…+ахnРn
3) Для удобства рассмотрим след. 2 случая:
ξ: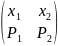 η:
η: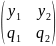 ξ+η:
ξ+η:
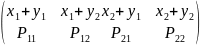
М[ξ+η] = (х1+у1) р11 + (х1+у2) р12 + (х2+у1) р21 + (х2+у2) р22 = х1(р11+ р12) + х2(р21+ р22) + у1(р11+ р21) + у2(р12+ р22) ;
1 2
р11+ р12 = р(ξ+η= х1+у1)+ р(ξ+η= х1+у2) = р(ξ=х1 и η=у1)+р(ξ=х1 и η=у2) = р(ξ=х1)= р1
аналогично доказывается, что р21+ р22= р2; р11+ р21= q1; р12+ р22 = q2
1: х1Р1+х2Р2 = mξ 2: у1q1+ у2q2 = m η М[ξ*η] = М[ξ]*М[η]
4)
ξ:
η:
ξ*η:

mξ =х1Р1+х2Р2; m η = у1q1+ у2q2
Тогда М[ξ*η]= х1у1 р1q1 + х1у2 р1q2+ х2у1 р2q1+ х2у2р2q2 = х1р1(у1q1 + у2q2) + х2р2(у1q1 + у2q2) = (у1q1 + у2q2)( х1р1+ х2р2) = m η* mξ
