2. 2. Интегрирование по частям
Этот прием
представляет сведение данного интеграла
к интегралу
с помощью формулы
Этот прием ведет к цели, если находится легче, чем .
Это правило хотя и имеет более ограниченную область применения по сравнению с заменой переменной, существует целый класс функций, который интегрируется именно с помощью этого метода. Сюда можно отнести:
где
- целое положительное число. Применение
метода интегрирования по частям
предусматривает последовательное
понижение степени
до нулевой.
Примеры:
2.2.1.
Найти интеграл
.
Применим формулу интегрирования по частям, обозначив
,
,
,
.
Тогда
2.2.2.
Найти интеграл:
Применяя дважды интегрирование по частям
В первый
раз,
обозначим:
,
,
,
,
получим
,
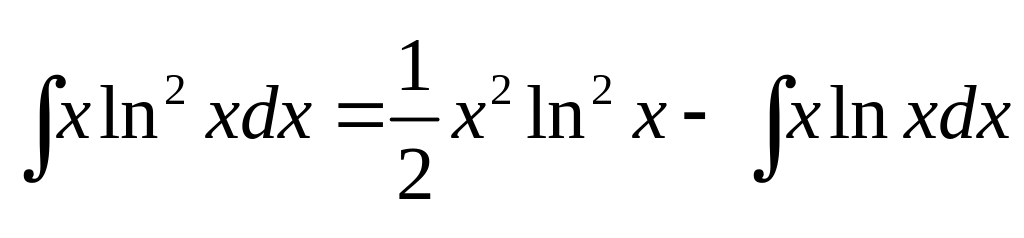а во второй раз:
,
,
,
,
получаем:
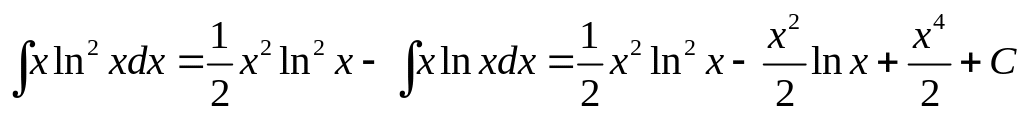
2.2.3.
Найти интеграл:
Обозначая
,
,
,
и применив в ходе вычисления замену
,
получим
2.2.4.
Найти интеграл:
■ Применим метод интегрирования по частям:
.◄
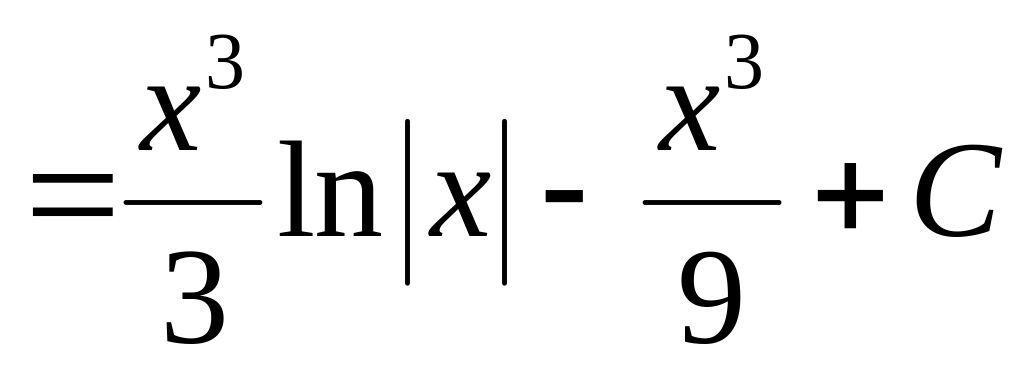2.2.5.
Найти интегралы:
и
.
■ Применим метод интегрирования по частям:
;
.
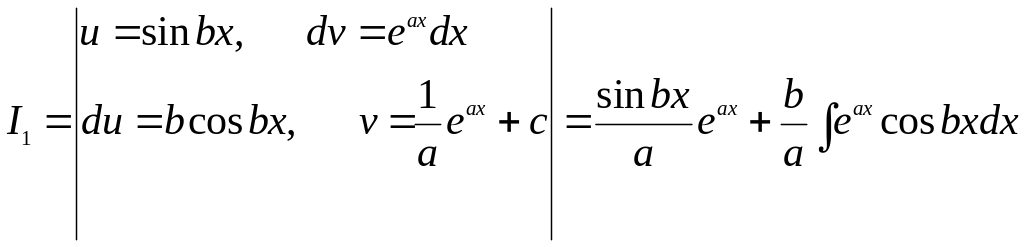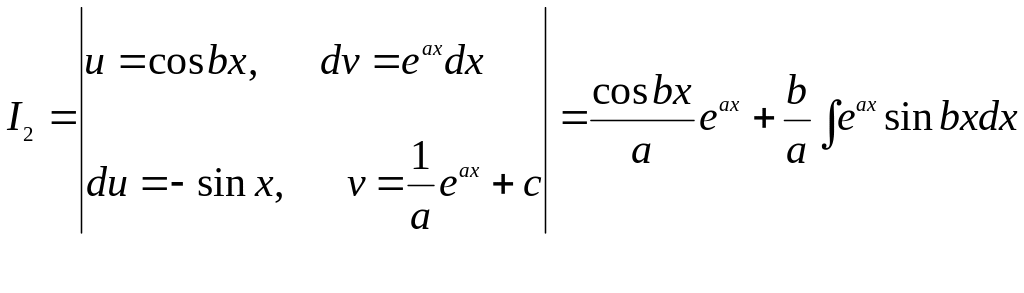Таким образом,
получается система линейных уравнений
относительно неизвестных
и
:
,
разрешая которую, получаем
.
2.3. Интегрирование простых дробей
К простым дробям относятся
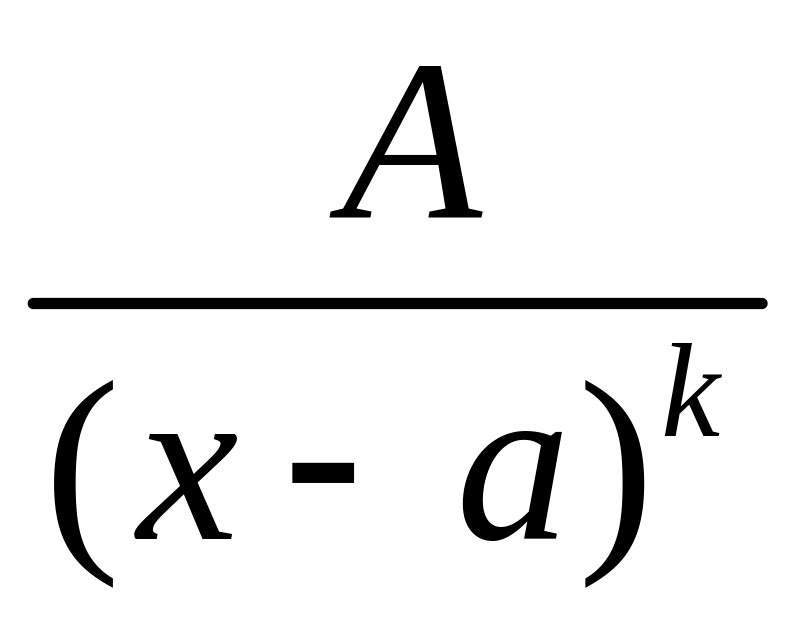(I)
;
(II)
;
(III)
;
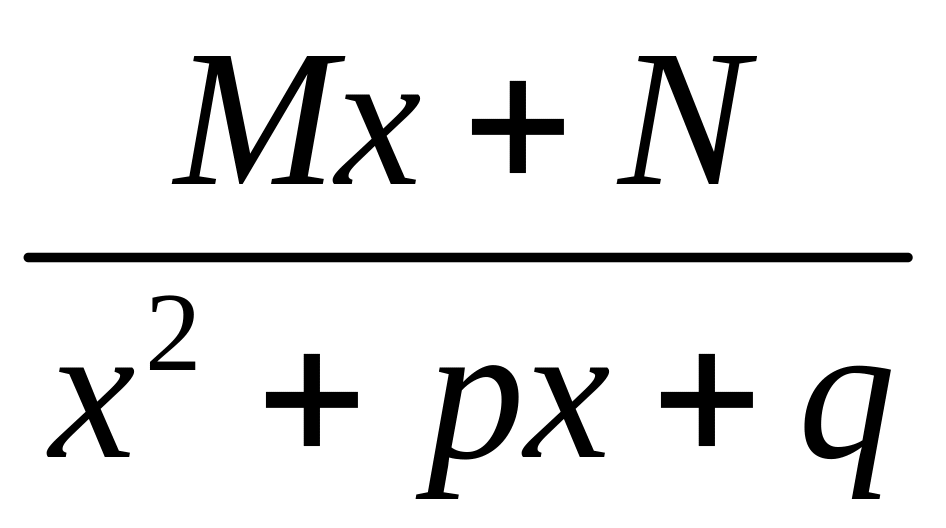(IV)
где
- действительные числа,
.
Кроме того, трехчлен
не имеет действительных корней, т.е.
Интегрирование (I) и (II) не представляет трудностей:
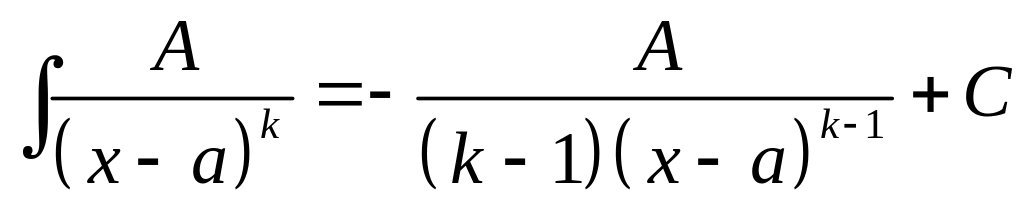
Для интегрирования дроби (III) применим метод замены переменной. Выделяя сначала из знаменателя полный квадрат
и прибегнув к подстановке
и обозначив
получаем
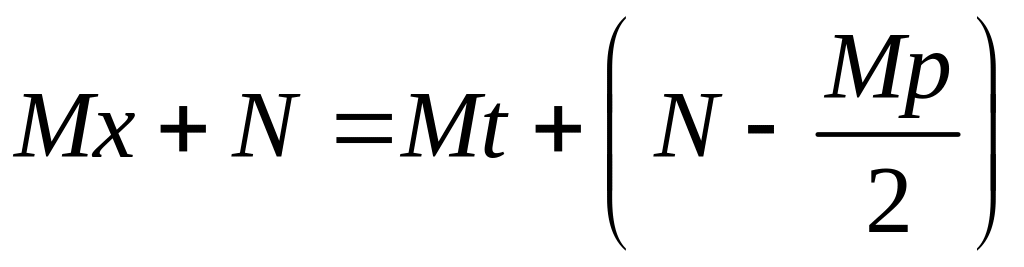
а сам интеграл
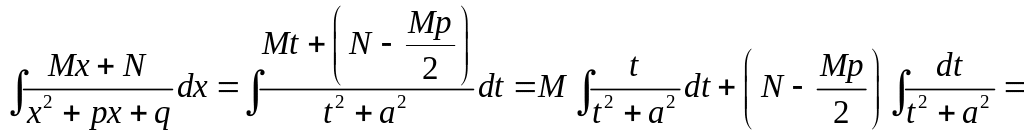
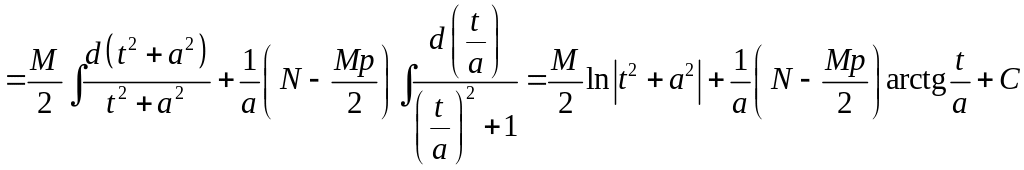
Возвращаясь обратно к переменной , окончательно получаем:
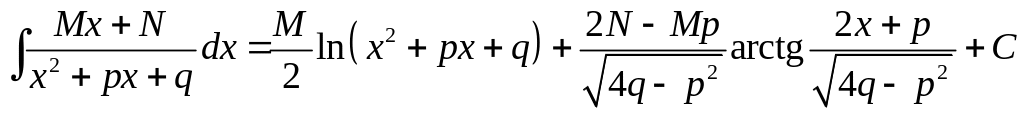
Для случая (IV) подстановка приводит
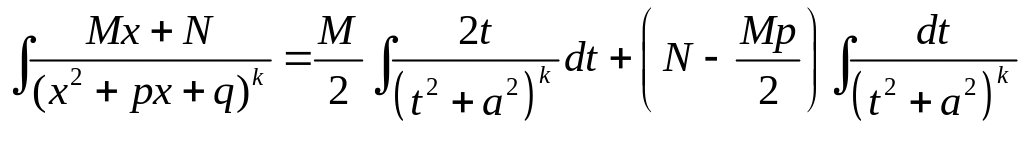
Первый интеграл
вычисляется подстановкой
,
:
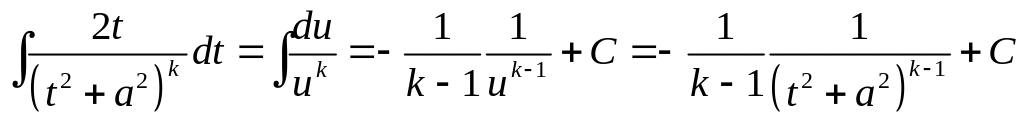
Второй интеграл вычисляется с помощью рекуррентной формулы
,
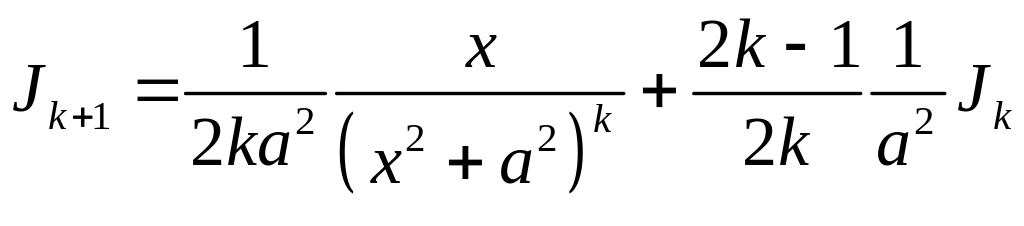где
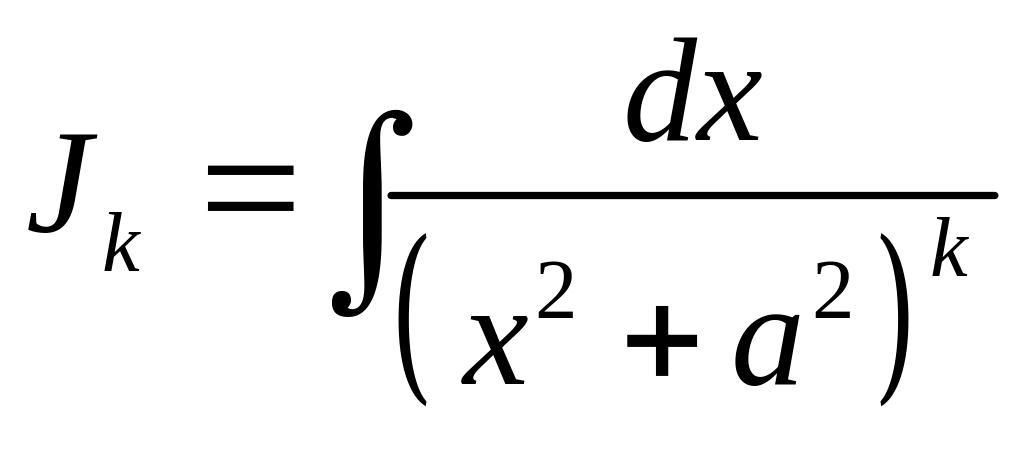
Приведенное
рекуррентное соотношение позволяет
найти искомый интеграл для любого
натурального индекса
.
Так как при
,
то,
и т.д.
Примеры:
2.3.1.
Найти интеграл:
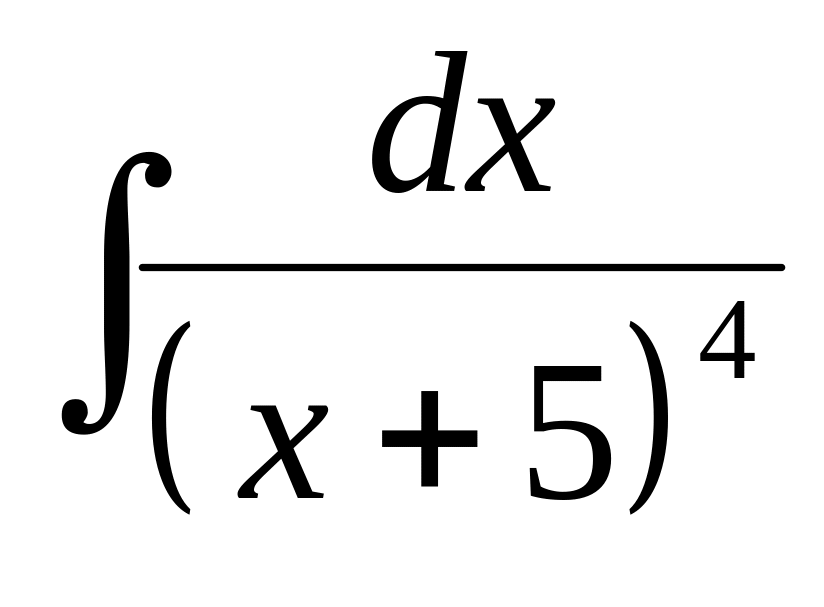
■ Интеграл относится
ко II
типу. Здесь
.
Применив формулу:
,
получим:
.◄
2.3.2.
Найти интеграл:
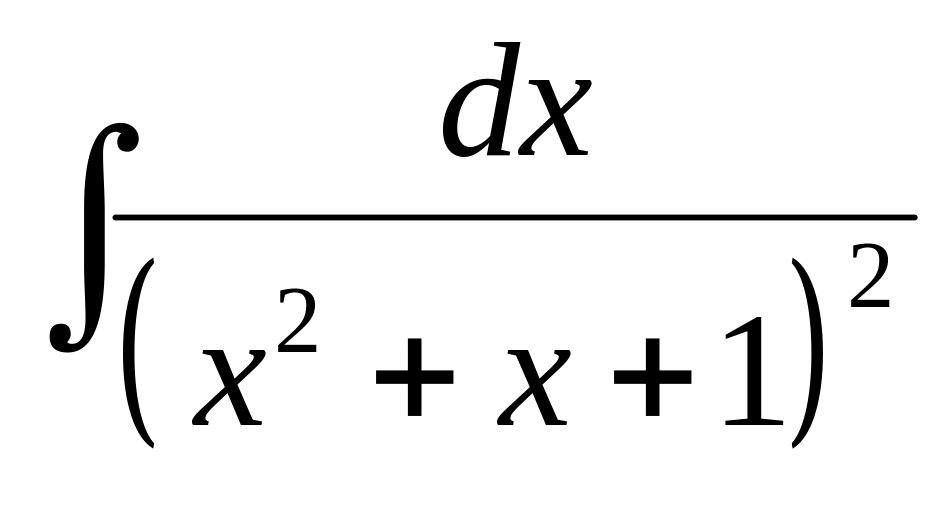
■ Интеграл
относится к IV
типу. Здесь
.
В знаменателе дроби исходного интеграла выделим неполный квадрат. Тогда:
.
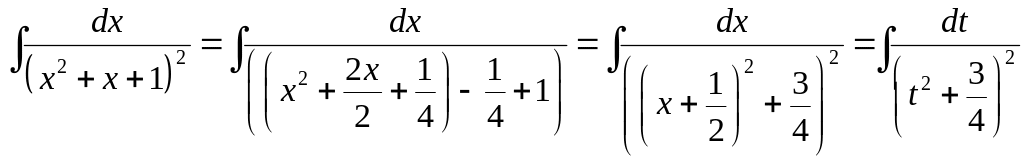Применим рекуррентную формулу:
.
При
;
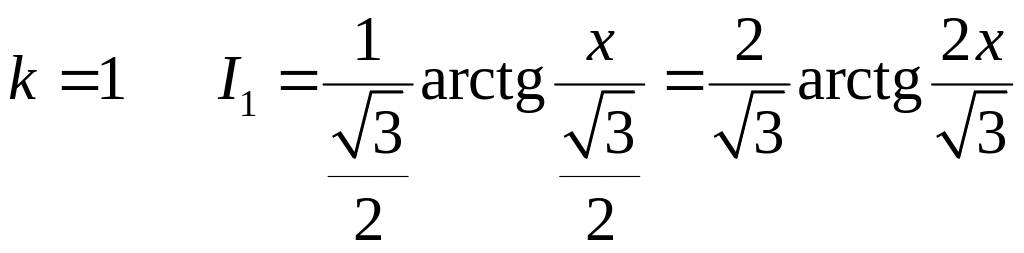При
.
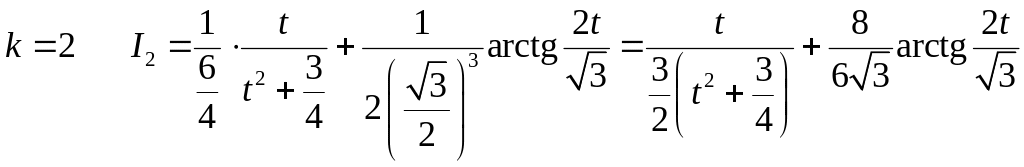
Тогда первоначальный интеграл примет вид:
.◄
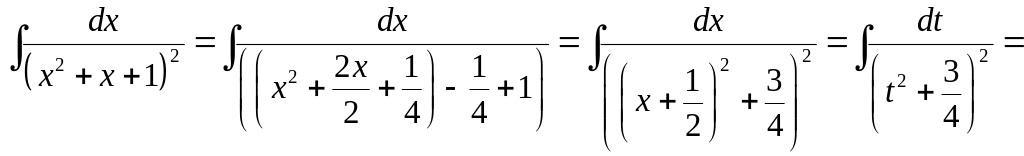
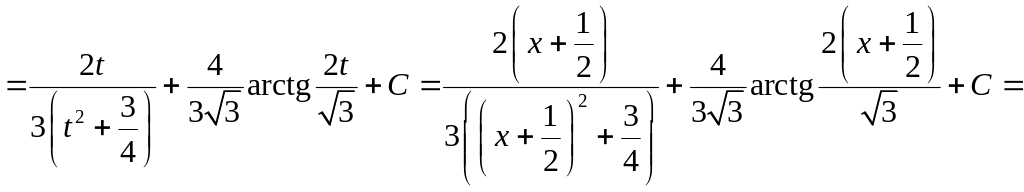
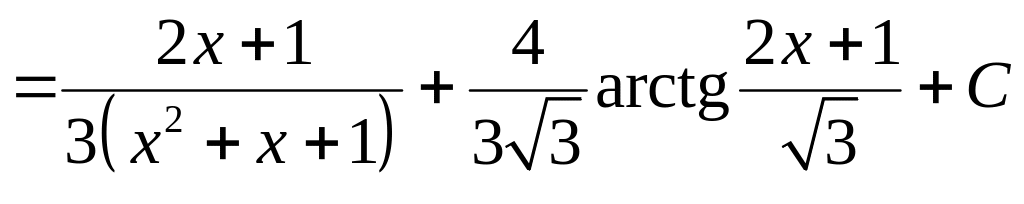2.3.3.
Найти интеграл:
■ Воспользовавшись примером 3.2., выделив неполный квадрат в знаменателе подынтегральной дроби и произведя замену, получим:
.
Интеграл относится
к (IV)
типу. Здесь
.
Применив рекуррентную формулу:
,
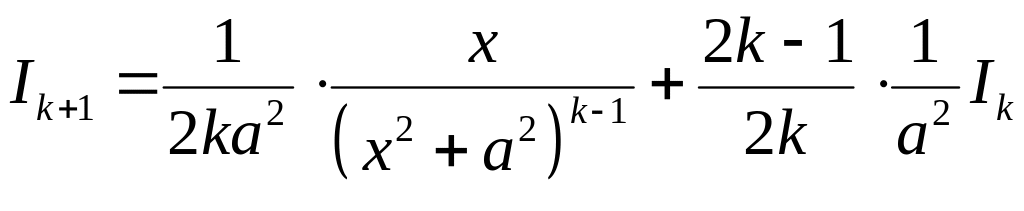получим:
.◄
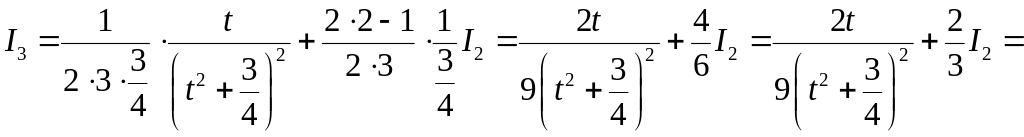
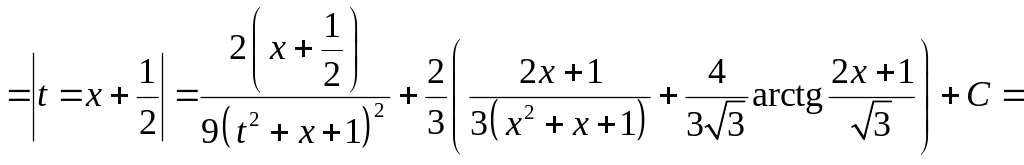
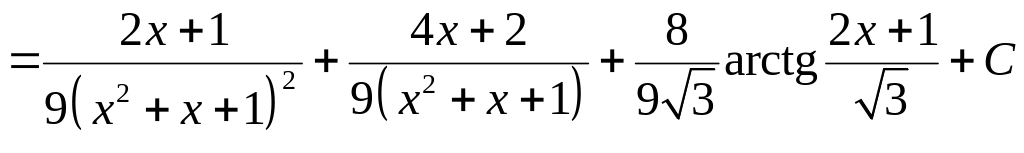2.3.4.
Найти интеграл:
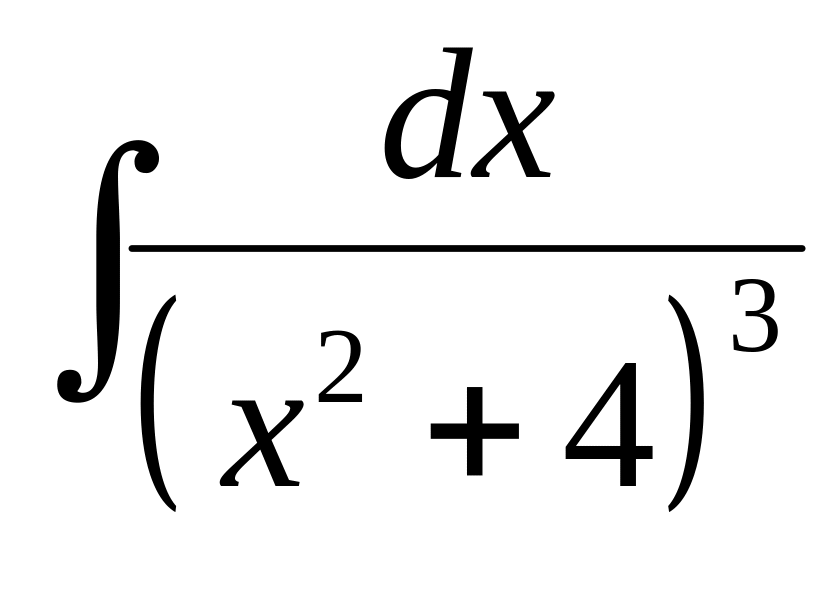
■ Здесь . Применяя рекуррентную формулу
,
получим:
При
;
При
.
Тогда искомый интеграл при будет равен:
◄
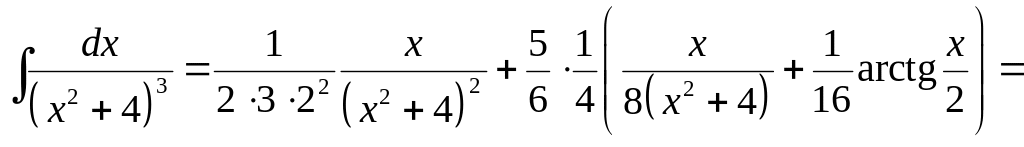
2.3.5.
Найти интеграл:
■ Преобразуем подынтегральное выражение.
.
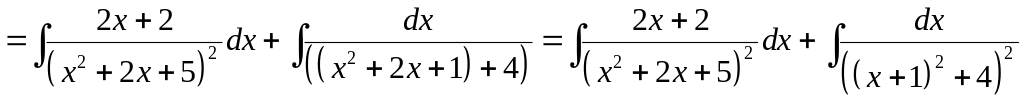Сделаем в первом
интеграле замену
,
во втором
.
Воспользовавшись примером 3.4., получим
,
.
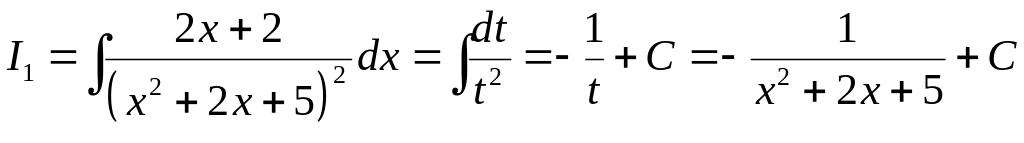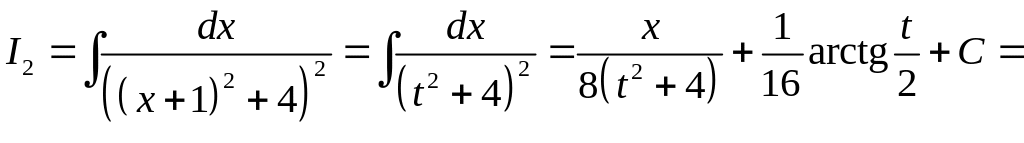
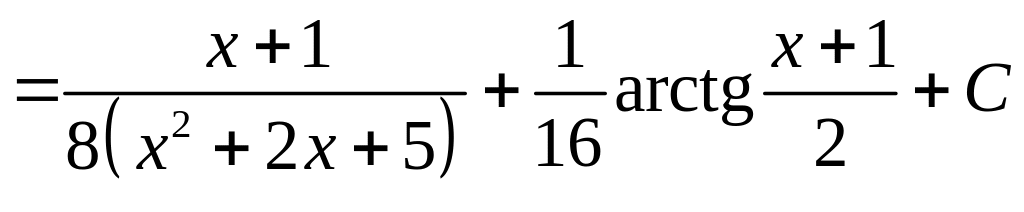Окончательно,
.◄
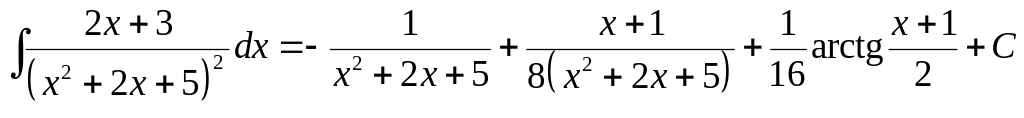