Глава 1

Вписанные и описанные многоугольники

51

Скачено с Образовательного портала www.adu.by

Теорема (о существовании окружности, описанной око­ло треугольника). Около любого треугольника можно описать единственную окружность.

Доказательство. {. Докажем, что около тре угольника можно описать окружность.

Рис. 47

1. Пусть ABC — произвольный тре­угольник, О — точка пересечения сере­динных перпендикуляров к его сторонам (рис. 47).

2. Так как точки серединного перпен­дикуляра к отрезку равноудалены от его концов, то ОА = ОВ = ОС. Таким образом,

окружность с центром в точке О радиуса ОА проходит через все вер­шины треугольника ABC, а значит, является описанной около этого треугольника.

II. Докажем, что такая окружность единственная.

Предположим, что около треугольника можно описать еще одну окружность. Тогда ее центр равноудален от вершин треугольника, а сле­довательно, совпадает с точкой О пересечения серединных перпендику­ляров к сторонам треугольника; ее радиус равен расстоянию от точки О до вершин треугольника. Таким образом, окружности совпадают.

Теорема доказана.

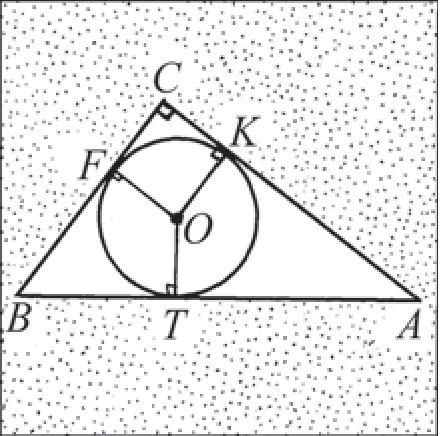
Задача 1. Докажите, что радиус г вписанной в прямоугольный треугольник окружности находится по формуле г = р — с, гдер — по­лупериметр прямоугольного треугольника, с — его гипотенуза.

■■■ А ^ш К і'-'ХТ;^1-^1■ ■ ■	(■Г:- ■ ■ ,<
	\	r = p-c
		\	'
	У
	'■.-■^vF::V;i-::v:.^;.£f '•j-i- -* La'-T^,.^r'»''!^L'.:- -г;

а)

б)

Дано: ААВС, ZACB = 90°, АВ = с, г — радиус вписанной окруж­ности, р — полупе­риметр. Доказать: г = р — с.

Рис. 48

Доказательство.

1) Пусть К, Т, F — точки касания окружности со сторонами треугольника, О — центр вписанной окружности (рис. 48, а, б).

Тогда четырехугольник CKOF — квадрат (так как Z ОКС = = Z KCF =Z CFO = 90°, СК= CF).

2. Отрезки касательных, проведенные из одной точки, равны, следовательно, АТ = АК=АС — г и ВТ = BF = ВС — г.

3. Так как AT + ВТ = с, то (АС — г) + (ВС — г) = с. Таким образом,

АС+ВС-с АС+ВС+с г = или г = — с=р — с.

2 2

Что и требовалось доказать.

Задача 2. Докажите, что в произвольном треугольнике ABC

a

2R, где a — сторона, лежащая про-

sin A радиус описанной окружности.

Дано: ААВС, ВС = а, R — ради ус описан­ной окружности.

Доказать:

а = 2R.

sin A

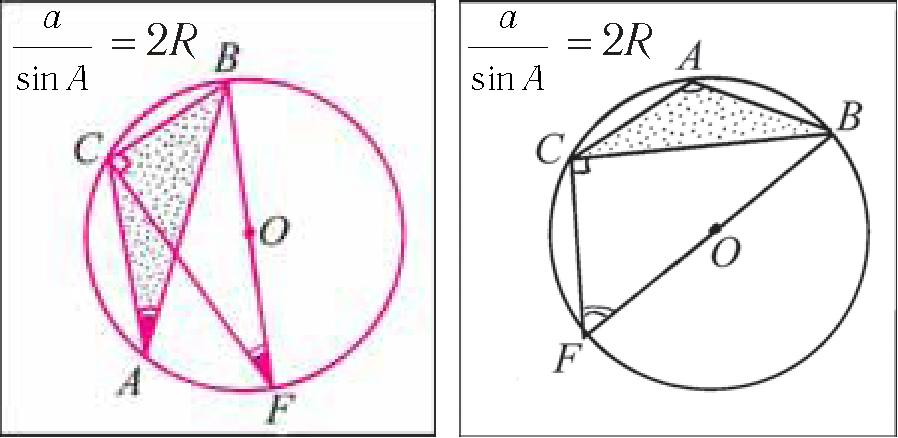
выполняется равенство тив угла A, а R

б)

а)

Рис. 49

Доказательство.

Пусть около треугольника ABC описана окружность. Проведем диаметр BF этой окружности. Возможны два случая.

ВС а BF 2R

Первый случай. Углы А и F опираются на одну дугу (рис. 49, а).

Тогда ZA = ZF. В прямоугольном треугольнике BCF sin F

. а а значит, sin Л = —. 2R Второй случай. Углы А и F опираются на дополнительные дуги,

т. е. ZA + ZF = 360° : 2 = 180° (рис. 49, б). Тогда ZF = 180°— ZA.

п^г- г- ВС а

В прямоугольном треугольнике ВСг sin г = — = —. Но так как

BF 2R sin F = sin (180° — Z А), то в этом случае также sin A

2R

52