Глава 1

Вписанные и описанные многоугольники

27

Градусная мера дуги АТВ, которая больше полуокружности и дополняет дугу АВ, меньшую полуокружности, до окружнос­ти, равна 360° — Z АОВ, где угол АОВ соответствует дуге АВ (рис. 20, в).

Понятие градусной меры дуги позволяет определить понятие ра­венства дуг окружности.

Две дуги одной и той же окружности называются равными, если равны их градусные меры.

Если градусная мера дуги АВ равна 33°, то пишут: yjAB = 33°. Читают: «Градусная мера дуги АВ равна 33°», или кратко «Дуга АВ равна 33°».

Рассмотрим примеры. Пусть даны квадрат ABCD, диагонали ко­торого пересекаются в точке О, и окружность со (С; СО) (рис. 21, а). Точки F и L — точки пересечения окружности со сторонами ВС и DC соответственно. Тогда yjFOL = 90°, а дуга FO, меньшая полуокруж­ности, равна 45°. Градусная мера дуги FLO, которая больше полу­окружности, равна 360° — Z FCO = 360° — 45° = 315°.

2. Вписанные углы. Рассмотрим понятие вписанного угла.

О п р е д е л е н и е. Угол называется вписанным в окружность, если он меньше развернутого угла, вершина его лежит на окруж­ности, а стороны пересекают эту окружность.

б) Рис. 22

а)

в)

Например, на рисунке 22, а изображен вписанный угол TOF. Если точки A, B и С лежат на окружности, то каждый из углов ABC, BCA, CAB является вписанным (рис. 22, б).

В	Ff	С
	\1 /'
	zV-н	L
я ^1—

а)

б)

Рис. 21

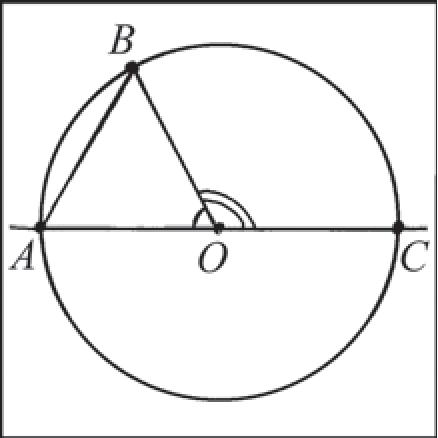
Рассмотрим еще один пример. Пусть АВ — хорда окружности, равная ее радиусу, а АС — диаметр окружности с центром в точке О (рис. 21, б). Тогда дугаЛ/3, меньшая полуокружности, имеет градусную меру 60°, так как треугольник АОВ — равносторонний, а, значит, соответствующий ей центральный угол АОВ равен 60°. Дуга ВС, меньшая полуокружности, равна 120°, так как соответствующий ей центральный угол ВОС равен 120°. Дуга ВАС больше полуокружности, следовательно, yjBAC = 360° — Z ВОС = 360° — 120° = 240°.

Скачено с Образовательного

Пусть TOF — вписанный угол, при этом Г и F — точки пересече­ния его сторон с окружностью, а TF — дуга, которая лежит внутри это­го вписанного угла. В этом случае говорят, что вписанный угол TOF опирается на дугу ТУ⁷ (см. рис. 22, а). Например, на рисунке 22, в изображены вписанные углы ВАС, ВОС и BFC, которые опираются на одну и ту же дугу ВС.

Теперь докажем теорему о вписанном угле.

Теорема 1 (о вписанном угле). Градусная мера вписан­ного угла равна половине градусной меры дуги, на которую он опирается.

Доказательство.

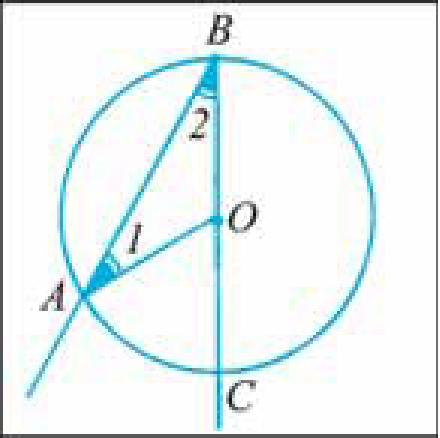
Пусть ABC — угол, вписанный в окруж­ность с центром в точке О, который опирается

на дугу АС. Докажем, что Z ABC = — kjAC.

2 Рассмотрим три возможных случая.

Первый случай. Луч ВО совпадает с

одной из сторон угла ABC, например со

Рис. 23

стороной ВС (рис. 23).

портала www.adu.by

28