Глава 1

Вписанные и описанные многоугольники

63

того, по условию АВ + CD = BF + FC + AD. Отсюда следует, что АВ + CD = АВ + DF + FC или CD — DF = FC, что невозможно, так как в треугольнике DFC сторона FC должна быть больше разности двух других сторон. Аналогично приводит к противоречию и предположение о том, что сторона CD является секущей.

5) Таким образом, предположение о том, что сторона CD не касается рассматриваемой окружности, неверно. Следовательно, сторона CD касается этой окружности, и, значит, окружность вписана в четырехугольник ABCD. Теорема доказана.

2. Окружность, описанная около четырехугольника. Определим понятие окружности, описанной около четырехугольника.

Определение. Окружность называется описанной около че­тырехугольника, если все его вершины лежат на окружности. В этом случае четырехугольник называется вписанным в окружность.

Теперь рассмотрим свойство четырехугольника, вписанного в окружность.

Теорема 3 (о свойстве четырехугольника, вписанного в окружность). Если около четырехугольника описана окружность, то суммы градусных мер его противолежащих углов равны 180°.

	^вг—■£.
	f /:'■ '-'■-.'^у^'.\\ ^\.
	£'•"■':^:"'-'Л'-:'-'^\ \
^А\
	^fc /
	^*-—-^Ь

Доказательство.

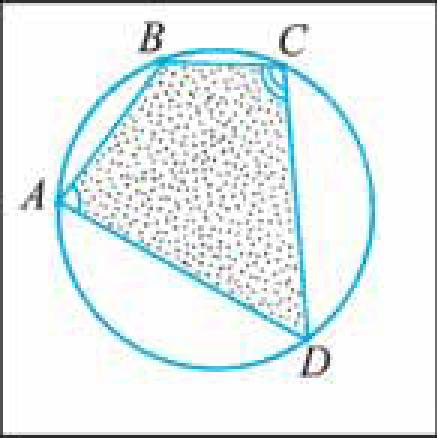
1. Пусть четырехугольник ABCD впи­сан в окружность (рис. 56). Докажем, что ZA + ZC =\ 80° и Z В + ZD = 180°.

2. Так как углы Л и С — вписанные, то

ZA =lj BCD и Z С=^и BAD. Таким об-

2 2

разом, ZA + Z С=^и BCD + kj BAD =

2 2

Рис. 56

= — (lj BCD + lj BAD) = — 360°= 180°.

2 2

Так как сумма углов четырехугольника ABCD равна 360° и Z А + Z С= 180°, то ZB + ZD = 180°. Теорема доказана.

Справедливо и обратное утверждение, характеризующее условие, при котором можно описать окружность около четырехугольника.

[Теорема 4 (условие, при котором около четырехуголь­ника можно описать окружность) ]. Если в четырехугольнике сумма градусных мер противолежащих углов равна 180°, то около такого четырехугольника можно описать окружность.

Скачено с Образовательного

а) б)

Рис. 57

Доказательство.

1. Пусть в четырехугольнике ABCD выполняется равенство ZA + ZC = 180°. Докажем, что около четырехугольника ABCD можно описать окружность (рис. 57, а).

2. Рассмотрим окружность, описанную около треугольника ABD, и докажем, что эта окружность проходит также через вершину С. Предположим, что окружность не проходит через вершину С. Тогда либо вершина С лежит вне круга, границей которого служит рассмат­риваемая окружность, либо внутри этого круга.

3. Пусть вершина С лежит вне круга (рис. 57, б). Обозначим буквами F и О точки пересечения сторон ВС и DC с окружностью.

Тогда Z С = (и DAB — lj FO). Следовательно, Z С < lj DAB. Так

2 2

— lj BOD, а значит, ZA + ZC<

2

180°.

как угол А вписанный, то Z А =

^ 1 / г,ґ~* ^- 360°

(lj BUD + lj DAB) < =

2 2

Это противоречит условию, значит, наше предположение не вер­но, т. е. окружность проходит через вершину С. Аналогично можно доказать, что вершина С не может лежать внутри круга.

Теорема доказана.

Из доказанной теоремы следует, что около любого прямоуголь­ника можно описать окружность.

Рассмотрим некоторые задачи, при решении которых используются доказанные теоремы.

Задача 1. Около окружности описана равнобедренная трапеция ABCD, длина ее боковой стороны равна 10 см, а угол при основании трапеции равен 60°. Вычислите площадь трапеции.

портала www.adu.by

64