Теоретический материал:

Численное дифференцирование используется для приближенного вычисления производных функции заданной таблицей и для функций, которые по разным причинам неудобно или невозможно дифференцировать аналитически. В последнем случае вычисляется таблица функции в окрестности исследуемой точки и по этим значениям вычисляется приближенное значение производной.

Рассмотрим численный метод решения дифференциального уравнения первого порядка вида у'=f(x,y), который носит название метода Эйлера.

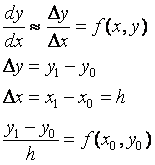
y1=y0+h*f(x0,y0) x1=x0+h	Расчетные формулы для 1-го шага
yi+1=yi+h*f(xi,yi) xi+1=xi+h	Расчетные формулы для i-го шага

Примеры вычислений

Дано у'= xy², x₀=0, y₀ =2, (или по другому y(0)=2), h=0,1. Найти с точностью до десятых y(0,2) (т.е. y₂).

Алгоритм решения поместим для удобства в таблицу.

шаг i	xi	yi	у'= xiyi^2	Δy=h*f(xi,yi)
0	0	2	0·2^2=0	0,1·0=0
1	0+0,1=0,1	2+0=2	0,1·2^2=0,4	0,1·0,4=0,04
2	0,1+0,1=0,2	2+0,04=2,04⋲2

Ответ: y(0,2)⋲2

Задание для практической работы по теме «Решить приближенно дифференциальное уравнение вида y'=f(x,y) с начальным условием y(x₀)=y₀ (задачи Коши) методом Эйлера»

Вычислить значение y(0,3) для функции заданного вида с начальными условиями y(0)=2 методом Эйлера.

Вариант 1. у'=y-x²y,

Вариант 2. у'=y+x²y

Вариант 3. у'=(1-2x)·y²

Вариант 4. у'=(1-x²)·y

Вариант 5. у'=(y²-y)·x

Вариант 6. у'=4x-2y

Вариант 7. у'=2x-y

Вариант 8. у'=x+3y

Вариант 9. у'=4x+y

Вариант 10. у'=3x-2y+5

Практическая работа № 18

Тема 4.3: "Приближенное вычисление значения функции y(X) в точке с помощью производной".

Цель: Вычислять приближенное значения функции y(x) в точке с помощью производной.

Теоретический материал:

Вспомним уравнение касательной к графику функции f(x) в точке с абсциссой . Объяснение по графику и записи рисунка. Каково взаимное расположение точек графика функции и точек касательной вблизи точки касания с абсциссой ? (Ответ: очень близко расположены). Что это означает? Если функция y= f(x) дифференцируема в точке , то значения функции в точках из окрестности точки  очень мало отличаются от значений функции, задающей уравнение касательной, и для всех значений х из окрестности точки  можно записать:

f(x)≈ .

Поскольку x, можно записать

f(x)≈ x

Пример вычисления

Пусть дана функция и надо найти её значение при х=2,03. Заметим, что при х = 2 легко вычислить f(2)= = 77.

Применяя выведенную формулу, получим: f(x)=f(2,03),

  , Δ x= х-x₀= 2,03-2 =0,03;

f(2,03)=77+172·0,03=77+5,16=82,16.

Если произвести вычисления на калькуляторе, то получается f(2,03)=82,297634. Как видим, приближенное значение, полученное при помощи формулы, очень мало отличается от точного значения функции в данной точке.

Задание для практической работы по теме «Приближенное вычисление значения функции y(x) в точке с помощью производной»

Вычислить:

1. приближенное значения функции y(x) с помощью производной;

2. точное значения функции y(x) с помощью ПК или калькулятора;

3. абсолютную и относительную погрешность.

Вариант1: 1,04¹⁵

Вариант2:

Вариант3: 0,99¹⁵

Вариант4:

Вариант5: 1,04¹⁰

Вариант6:

Вариант7: 0,98²⁵

Вариант8:

Вариант9: 1,02⁵⁰

Вариант10:

Практическая работа № 19