
- •131018.51 « Разработка и эксплуатация нефтяных и газовых месторождений»
- •Аннотация
- •Введение
- •Раздел 1. Дифференциальное и интегральное исчисление.
- •Тема 1.1: «Вычисление производных функций».
- •Теоретический материал.
- •Правила дифференцирования:
- •Примеры вычисления производных.
- •Тема 1.2: «Нахождение углового коэффициэнта касательной к графику функции в указанной точке. Составление уравнения касательной.»
- •Теоретический материал:
- •Геометрический смысл производной функции в точке.
- •Составление уравнения касательной прямой
- •Тема 1.3: «Вычисление производных сложных функций».
- •Теоретический материал:
- •Примеры вычисления производных сложных функций.
- •Тема 1.4:«Вычисление производных высших порядков функции нескольких переменных».
- •Теоретический материал: Производные высшего порядка.
- •Тема 1.5:«Нахождение табличных интегралов. Вычисление интегралов с использованием их свойств и таблицы интегралов».
- •Теоретический материал:
- •Тема 1.6: «Применение формулы Ньютона-Лейбница, свойства определенного интеграла при вычислениях. Методы интегрирования по частям и подстановкой».
- •Теоретический материал: Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.
- •Формула интегрирования по частям:
- •Определенный интеграл
- •Примеры вычисления
- •Тема 1.7: «Геометрический смысл определенного интеграла. Вычисление площади плоской фигуры с помощью определенного интеграла»
- •Теоретический материал:
- •Тема 1.8: " Решение дифференциальных уравнений с разделяющимися переменными первого порядка "
- •Теоретический материал:
- •Примеры вычисления
- •Тема 1.9: "Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами"
- •Теоретический материал:
- •Алгоритм решения
- •Примеры вычисления
- •Тема 1.10: «Нахождение решения дифференциальных уравнений Бернулли».
- •Теоретический материал:
- •Примеры вычисления.
- •Раздел 2. Числовые ряды
- •Тема 2.1: «Вычисление членов числового ряда. Вычисление частичных сумм».
- •Теоретический материал:
- •Примеры вычисления
- •Задание для практической работы по теме «Вычисление членов числового ряда. Вычисление частичных сумм».
- •Тема 2.2: «Применение необходимого и достаточного признаков сходимости числовых рядов и признака Даламбера»
- •Теоретический материал:
- •Примеры вычисления
- •Тема 2.3: «Выделение знакоположительного, знакочередующегося и степенного ряда. Разложение элементарных функций по формуле Тейлора».
- •Теоретический материал:
- •Примеры вычислений
- •Понятие функционального ряда
- •Примеры вычислений
- •Разложение элементарных функций в ряд Маклорена
- •Раздел 3. ОСновы дискретной математики.
- •Тема 3.1: «Выполнение операций над множествами».
- •Тема 3.2: «определение основных характеристик графа».
- •Теоретический материал:
- •Раздел 4. Численное дифференцирование и интегрирование.
- •Теоретический материал
- •Теоретический материал:
- •Примеры вычислений
- •Тема 4.3: "Приближенное вычисление значения функции y(X) в точке с помощью производной".
- •Теоретический материал:
- •Пример вычисления
- •Тема 4.4: "Вычисление интегралов по формулам прямоугольников".
- •Теоретический материал:
- •Пример вычисления
- •Тема 4.5: " Вычисление интегралов по формулам трапеций ".
- •Теоретический материал:
- •Список литературы
Тема 1.5:«Нахождение табличных интегралов. Вычисление интегралов с использованием их свойств и таблицы интегралов».
Цель: Находить табличные интегралы, вычислять интегралы с использованием их свойств и таблицы интегралов.
Теоретический материал:
Определение. Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x X справедливо равенство:
F (x) = f(x).
Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение - f(x) dx.
Если F(x) - какая-нибудь первообразная для функции f(x), то
f(x)dx = F(x) + C,
где С - произвольная постоянная.
Свойства неопределенного интеграла:
1) d f(x)=f(x)dx, 2) df(x)=f(x)+C,
3) af(x)dx=a f(x)dx (a=const), 4) (f(x)+g(x))dx= f(x)dx+ g(x)dx
Таблица интегралов элементарных функций:
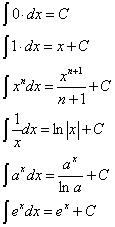
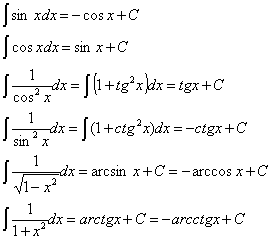
Задание для практической работы по теме « Нахождение табличных интегралов. Вычисление интегралов с использованием их свойств и таблицы интегралов».
Найти неопределенные интегралы используя таблицу интегралов и их свойств:
Вариант 1 |
Вариант 2 |
|
|
Вариант 3 |
Вариант 4 |
|
|
|
Вариант 5 |
Вариант 6 |
|
5.
|
5.
|
Практическая работа № 6
Тема 1.6: «Применение формулы Ньютона-Лейбница, свойства определенного интеграла при вычислениях. Методы интегрирования по частям и подстановкой».
Цель: Применять формулу Ньютона-Лейбница, свойства определенного интеграла при вычислениях. Освоить методы интегрирования по частям и подстановкой.
Теоретический материал: Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.
Например:
1)
![]() ;
;
2)![]() .
.
Формула интегрирования по частям:
udv = uv - vdu.
Пусть, например, требуется найти x cosx dx. Положим u = x, dv = cos x dx, так что du=dx, v=sinx. Тогда
x cos x dx = x d(sin x) = x sin x - sin x dx = x sin x + cos x + C.
Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,
xk lnmx dx, xk sin bx dx, xk cos bx dx, xk e ax dx
и другие, которые вычисляются именно с помощью интегрирования по частям.
Определенный интеграл
Понятие определенного
интеграла вводится следующим образом.
Пусть на отрезке [a, b] определена функция
f(x). Разобьем отрезок [a, b] на n частей
точками a = x0 < x1 <...<xn
= b. Из каждого интервала (xi1,
xi) возьмем произвольную точку i
и составим сумму
![]() f(i)
xi, где
xi = xi - xi1.
Сумма вида
f(i)
xi называется интегральной
суммой, а ее предел при
= max xi 0,
если он существует и конечен, называется
определенным интегралом функции f(x)
от a до b и обозначается:
f(i)
xi, где
xi = xi - xi1.
Сумма вида
f(i)
xi называется интегральной
суммой, а ее предел при
= max xi 0,
если он существует и конечен, называется
определенным интегралом функции f(x)
от a до b и обозначается:
![]()
![]() f(i)
xi.
(8.5)
f(i)
xi.
(8.5)
Функция f(x) в этом случае называется интегрируемой на отрезке [a, b], числа a и b носят название нижнего и верхнего предела интеграла.
Для определенного интеграла справедливы следующие свойства:
1)
![]()
![]() ;
;
2)
![]() ;
;
3)
-
![]() ;
;
4)
![]()
![]() , (k = const, kR);
, (k = const, kR);
5)
![]() ;
;
6)
![]() ;
;
7) f()(b-a) ([a,b]).
Последнее свойство называется теоремой о среднем значении.
Пусть f(x) непрерывна на [a, b]. Тогда на этом отрезке существует неопределенный интеграл
f(x) dx = F(x) + C
и имеет место формула Ньютона-Лейбница, связывающая определенный интеграл с неопределенным:
![]()
