
- •Действия над векторами.
- •Базис системы векторов.
- •Скалярное произведение векторов.
- •Векторное произведение векторов
- •Смешанное произведение векторов.
- •Плоскость в пространстве
- •Взаимное расположение плоскостей.
- •Нормальное уравнение плоскости
- •Общее уравнение прямой.
- •Нормированное уравнение прямой
- •Каноническое уравнение прямой
- •Уравнение прямой с угловым коэффициентом.
- •Взаимное расположение двух прямых на плоскости.
Действия над векторами.
1) Сложение векторов.
Опр. Суммой двух
векторов ![]() и
и ![]() является
диагональ параллелограмма, построенного
на этих векторах, исходящая из общей
точки их приложения (правило
параллелограмма).
является
диагональ параллелограмма, построенного
на этих векторах, исходящая из общей
точки их приложения (правило
параллелограмма).
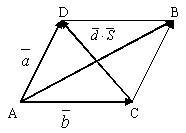
Рис.1.
Опр. Суммой трех
векторов
,
, ![]() называется
диагональ параллелепипеда, построенного
на этих векторах (правило параллелепипеда).
называется
диагональ параллелепипеда, построенного
на этих векторах (правило параллелепипеда).
Опр. Если А, В, С –
произвольные точки, то ![]() +
+ ![]() =
= ![]() (правило
треугольника).
(правило
треугольника).
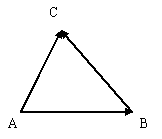
рис.2
2) Вычитание векторов.
Опр. Под разностью векторов
и
понимают
вектор ![]() =
–
такой,
что
+
=
.
=
–
такой,
что
+
=
.
В параллелограмме – это другая диагональ СД (см.рис.1).
3) Умножение вектора на число.
Опр. Произведением вектора на скаляр k называется вектор
= k = k,
имеющий длину ka, и направление, которого:
1. совпадает с направлением вектора , если k > 0;
2. противоположно направлению вектора , если k < 0;
3. произвольно, если k = 0.
Свойства умножения вектора на число.
1о. (k + l) = k + l .
k( + ) = k + k .
2o. k(l ) = (kl) .
3o. 1×
=
, (–1) ×
=
–
, 0 ×
= ![]() .
.
Свойства сложения
1о. + = + (переместительный закон).
2о. + ( + ) = ( + ) + = ( + ) + (сочетательный закон).
3о. + (– ) + .
Свойства умножения вектора на число.
1о. (k + l) = k + l .
k( + ) = k + k .
2o. k(l ) = (kl) .
3o. 1× = , (–1) × = – , 0 × = .
ЛЗ система векторов.
Определение.
Любой вектор вида ![]() =
=![]() называется
линейной комбинацией векторов
называется
линейной комбинацией векторов ![]() .
Числа
.
Числа ![]() - коэффициентами
линейной комбинации.
- коэффициентами
линейной комбинации.
Определение. Система векторов называется линейно-зависимой, если хоть один вектор системы может быть как линейная комбинация остальных векторов. В противном случае систему называют линейно-независимой.
Пример.
Система векторов ![]() линейно-зависима,
т. к. вектор
линейно-зависима,
т. к. вектор ![]() .
.
ЛНЗ система векторов.
Определение. Система векторов называется линейно-независимой, если ни один вектор системы не может быть как линейная комбинация остальных векторов.
Коллинеарность и компланарность векторов.
Опр. Два вектора и называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.
Нулевой вектор коллинеарен любому вектору.
Теорема. Два ненулевых вектора и коллинеарны, Û когда они пропорциональны т.е.
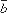 = k
, k –
скаляр.
= k
, k –
скаляр.
Опр. Три вектора , , называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
Теорема. Три ненулевых вектора , , компланарны, Û когда один из них является линейной комбинацией двух других, т.е.
= k + l , k ,l – скаляры.
Базис системы векторов.
Определение. Под системой векторов понимают несколько векторов, принадлежащих одному и тому же пространству R.
Определение. Любой вектор вида = называется линейной комбинацией векторов . Числа - коэффициентами линейной
комбинации.
Пример. ![]() .
.
Определение.
Если вектор ![]() является
линейной комбинацией векторов
является
линейной комбинацией векторов ![]() , то
говорят, что вектор
, то
говорят, что вектор ![]() линейно
выражается через векторы
.
линейно
выражается через векторы
.
Определение базиса. Система векторов образует базис, если:
1) она линейно-независима,
2) любой вектор пространства через нее линейно выражается.
Пример
1) Базис пространства ![]() :
: ![]() .
.
Пример
2) В системе векторов
базисом являются векторы: ![]() ,
т.к.
линейно
выражается через векторы
,
т.к.
линейно
выражается через векторы ![]() .
.
