5.2. Устойчивость нелинейных систем

В основе методов расчета устойчивости нелинейных систем лежит теория устойчивости движения, основанная А.М. Ляпуновым. Рассмотрим определение устойчивости движения, данное А.М. Ляпуновым. Пусть движение САУ описывается системой n дифференциальных уравнений первого порядка

, (5.7)

где – переменные, характеризующие поведение системы; – нелинейные функции своих аргументов.

Будем полагать, что в уравнении (5.7) отсчет значений переменных ведется от значений этих переменных в исследуемом на устойчивость движении, где они равны нулю. Это исследуемое на устойчивость движение называется невозмущенным движением (в частном случае это состояние равновесия). При указанном отсчете переменных уравнения (5.7) принято называть уравнениями возмущенного движения (уравнениями переходного процесса).

Невозмущенное движение описывается частным решением системы (5.7)

(5.8)

соответствующим нулевым начальным условиям.

Если при хотя бы часть переменных имеет отличные от нуля значения:

в теории устойчивости называемые возмущениями, то соответствующее этим возмущениям частное решение системы (5.7)

(5.9)

будет описывать движение, называемое возмущенным движением системы.

Определение. Невозмущенное движение, описываемое решением (5.8), называется устойчивым по Ляпунову относительно переменных , если для любого заданного положительного числа , как бы мало оно ни было, можно подобрать положительное число такое, чтобы при возмущениях, удовлетворяющих неравенствам

(5.10)

соответствующее этим возмущениям решение (5.9) для любого удовлетворяло бы неравенствам

(5.11)

Если дополнительно соблюдаются равенства

, (5.12)

то невозмущенное движение называется устойчивым по Ляпунову асимптотически. Если же для какого-нибудь положительного названного числа не существует, невозмущенное движение называется по Ляпунову неустойчивым.

Эти определения не меняются, если имеется в виду частный случай невозмущенного движения – состояние равновесия.

Иными словами, невозмущенное движение будет устойчивым, если при достаточно малом начальном отклонении любое возмущенное движение будет достаточно близким к невозмущенному. Примером устойчивого движения по Ляпунову может служить скатывание шарика по желобу, примером неустойчивого движения – скатывание того же шарика по ребру пирамиды.

Неустойчивые по Ляпунову движения и состояния равновесия могут получиться лишь при рассмотрении математических моделей, всегда идеализированных, физически же осуществимы только устойчивые по Ляпунову движения и состояния равновесия. Поэтому, если требуется, чтобы данный установившийся режим в системе фактически существовал, он должен быть рассчитан как устойчивый по Ляпунову.

Может оказаться, что при малых начальных отклонениях возмущенные движения будут приближаться к невозмущенному, а при больших начальных отклонениях – удаляться от него. В таком случае невозможно отыскать число , превосходящее некоторую величину, при котором бы неравенства (5.10) и (5.11) были справедливы для любого заданного числа .

Наибольшее положительное число , при котором невозмущенное движение остается устойчивым по Ляпунову, ограничивает некоторую область начальных отклонений – область сходимости возмущенных движений к невозмущенному. Если число , ограничивающее область сходимости, сколь угодно мало, невозмущенное движение называют устойчивым в малом, если это число достаточно велико – устойчивым в большом. Наконец, если невозмущенное движение асимптотически устойчиво по Ляпунову и область сходимости неограничена, то невозмущенное движение называют устойчивым в целом.

5 .2.1. Структурные схемы нелинейных систем. К нелинейной системе, содержащей хотя бы одно нелинейное звено, не применим принцип суперпозиции. При составлении структурной схемы выделяют нелинейное звено (или звенья) и линейные звенья, которые по известным правилам структурных преобразований могут быть представлены в виде одного эквивалентного звена. Таким образом, структурная схема нелинейной системы будет состоять из линейной ЛЧ и нелинейной НЧ частей, характеризуемых соответствующей передаточной функцией и нелинейной зависимостью , как это показано на рис. 5.2.

Наиболее часто на практике приходиться рассматривать САУ с одним нелинейным звеном, позволяющим оценить влияние различных типов нелинейностей на процесс управления. Путем структурных преобразований можно независимо от места включения нелинейного элемента привести структурную схему к виду, показанному на рис. 5.2.

Поясним характер структурных преобразований на примере одноконтурной следящей системы с одним нелинейным звеном и линейных звеньев с передаточными функциями, как это показано на рис. 5.3. Преобразования структурной схемы сводятся к нахождению согласующих звеньев, ввод которых сохраняет неизменным прохождение сигналов через систему. При этом должно соблюдаться условие как неизменности выходного и входного сигналов всей системы, так и нелинейного соотношения между входом и выходом нелинейного звена.

Если перенести линейное звено с передаточной функцией на вход сумматора, рис. 5.4 а, а затем выделить линейную часть в виде эквивалентного звена с передаточной функцией , в структурной схеме появятся два согласующих звена с передаточными функциями и , рис. 5.4 б. Таким образом, преобразованная структурная схема имеет замкнутый контур, включающий нелинейную часть НЧ в виде нелинейного звена и линейную часть ЛЧ с передаточной функцией .

Часто для уменьшения влияния нелинейной характеристики, как мы уже упоминали, нелинейное звено охватывают местной обратной связью. Примером может служить ввод отрицательной обратной связи в следящей системе рулевого привода судна.

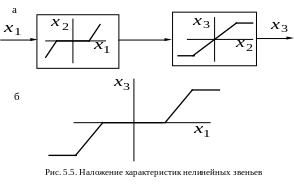В САУ может входить несколько нелинейных звеньев, включенных последовательно или параллельно. Два последовательно соединенных звена можно заменить в структурной схеме одним нелинейным звеном. Характеристику такого звена можно найти графическим способом. С этой целью характеристики нелинейных звеньев, выполненные в одном масштабе, накладывают друг на друга в последовательности прохождения сигнала при неизменности осей, характеризующих для каждого звена выходной и входной сигналы. Эта операция показана на рис. 5.5.

5.2.2. Метод гармонической линеаризации. Основным инженерным методом исследования устойчивости нелинейных САУ и САР является метод гармонической линеаризации Е.П. Попова и Л.С. Гольдфарба. Он позволяет выявить условия устойчивости, режимы возможных периодических колебаний, а также частоту и амплитуду колебаний.

При подаче на вход нелинейного звена синусоидального входного сигнала на его выходе появляется периодическое движение , которое будет содержать весь спектр гармоник в виде

где – коэффициенты разложения в ряд Фурье. Если статическая характеристика нелинейного звена симметрична относительно начала координат (см. рис. 5.1), то постоянная составляющая отсутствует.

Предполагая, что высшие гармоники фильтруются последующими в САР линейными звеньями и, выделяя первую гармонику, получим

,

где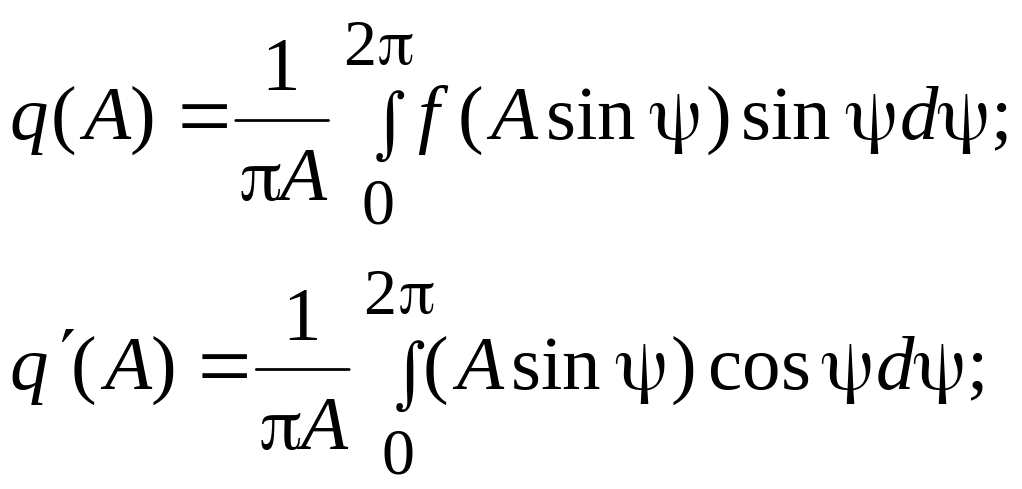

– угловая координата.

и – гармонические коэффициенты усиления нелинейного звена. Они вычисляются как коэффициенты первой гармоники при разложении в ряд Фурье величины , поделенные на амплитуду А. Изображение выходной величины согласно таблице изображений [2, 3] будет иметь вид:

Если входной сигнал синусоидален, то реакцию на него (по первой гармонике) можно определить с помощью передаточной функции нелинейного звена после замены :

(5.13)

Выражение (5.13) означает, что передаточная функция не зависит от частоты входного сигнала, а определяется его амплитудой. Поэтому можно записать, что

Годограф вектора , построенный на комплексной плоскости, называется амплитудной характеристикой нелинейного звена. Модуль этой характеристики

показывает, во сколько раз амплитуда первой гармоники на выходе нелинейного звена отличается от амплитуды входного синусоидального сигнала. Угол

выражает разность фаз выходного и входного сигналов.

Вычисление гармонических коэффициентов и производится по статической характеристике нелинейного звена. Для типовых нелинейностей эти коэффициенты вычислены и приведены в справочной литературе. Так, для трехпозиционного реле с зоной гистерезиса (рис. 5.1 л) коэффициенты и имеют вид:

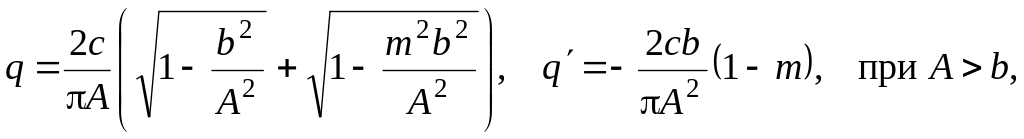
где m – коэффициент возврата (часто принимается m = 1).

Рассмотрим применение метода гармонической линеаризации для нелинейной САР, состоящей из линейной части и нелинейного звена и показанной на рис. 5.6.

В соответствии с рис. 5.6, имеем

Полагая, что на выходе нелинейного звена доминирует первая гармоника, найдем условия, которым должны удовлетворять параметры контура при наличии в нем незатухающих колебаний.

Уравнение свободного движения САР будет иметь вид:

(5.14)

Уравнение (5.14) довольно просто решается графически. Для этого перепишем его в виде:

(5.15)

Е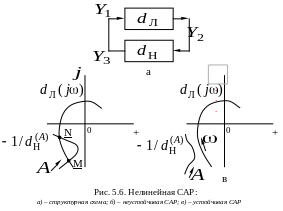 сли указанные характеристики пересекаются на комплексной плоскости, то это значит, что в САР возможны автоколебания (колебания с постоянной амплитудой). Точка пересечения на характеристике определяет частоту автоколебаний, а амплитуду незатухающих колебаний необходимо снять с характеристики Это обстоятельство графически представлено на рис. 5.6 б и в. На рис. 5.6 в показаны непересекающиеся характеристики. Это соответствует устойчивой нелинейной САР при отсутствии автоколебательного режима. Если характеристики пересекаются несколько раз (рис. 5.6 б), то надо уточнить, какая из точек пересечения характеризует параметры незатухающих колебаний. Точка пересечения характеристик будет соответствовать автоколебательному режиму, если обратная отрицательная амплитудная характеристика будет «выходить» из области, охваченной АФХ, с возрастающей амплитудой. В точке М характеристика «входит» в область, охваченной с возрастающей амплитудой. Значит, не точка М, а точка N является характерной для незатухающих колебаний. Это, достаточно не строгое правило, часто применяется на практике.

б