5.3. Релейные системы

Система, имеющая один или несколько релейных элементов, характеристики всех остальных звеньев которой линейны, называется релейной системой. Примером такой системы может служить система управления рулем, имеющая в своем составе электрогидравлический кран, распределяющий жидкость в полости силового цилиндра, перекладывающего в свою очередь руль, представленная на рис. 5.7. Кран является трехпозиционным. В среднем положении золотник перекрывает доступ жидкости из напорной магистрали в полости силового цилиндра. В крайнем левом или в крайнем правом положении жидкость из напорной магистрали поступает в левую или правую полости силового цилиндра, скачком обеспечивая максимальную скорость перекладки руля. На рис. 5.8 представлена характеристика скорости перекладки руля в зависимости от величины и знака управляющего воздействия (сигнала), имеющая релейный характер и зону нечувствительности, которая определяется жесткостью пружины. Допустим уравнение движения пл по курсу имеет вид

, (5.16)

г де: T – постоянная времени объекта управления, y – управляемая величина,  – положение исполнительного органа (руля), – возмущающее воздействие.

Положение исполнительного органа  является функцией управляющего воздействия  , которое зависит от управляемой величины y (например, рассогласование по курсу) и обратной связи системы по положению руля управления :

, (5.17)

где и – коэффициенты усиления, y – рассогласование истинного и заданного положения управляемой координаты.

При , где – заданное значение управляемой величины.

Релейный элемент – исполнительный привод – имеет уравнения движения следующего вида (рис. 5.8):

, (5.18)

где – постоянная времени релейного элемента, b – половина ширины его мертвой зоны.

На рис. 5.9 б представлена диаграмма работы такого привода, имеющего зону нечувствительности  b при подаче на его вход сигнала , изменяющегося по случайному закону (рис. 5.9 а).

5.3.1. Построение переходного процесса в релейной системе методом припасовывания. Рассмотрим способ построения переходных процессов в релейных системах на основе представленных выше уравнений релейной системы.

Изучая свободные колебания системы, положим , считая отличными от нуля начальные условия. Пренебрегаем мертвой зоной исполнительного привода ввиду ее малости, положив . Заметим также, что при , условие равносильно условию , а условие – условию . С учетом сделанных замечаний система уравнений (5.16–5.18) запишется в виде

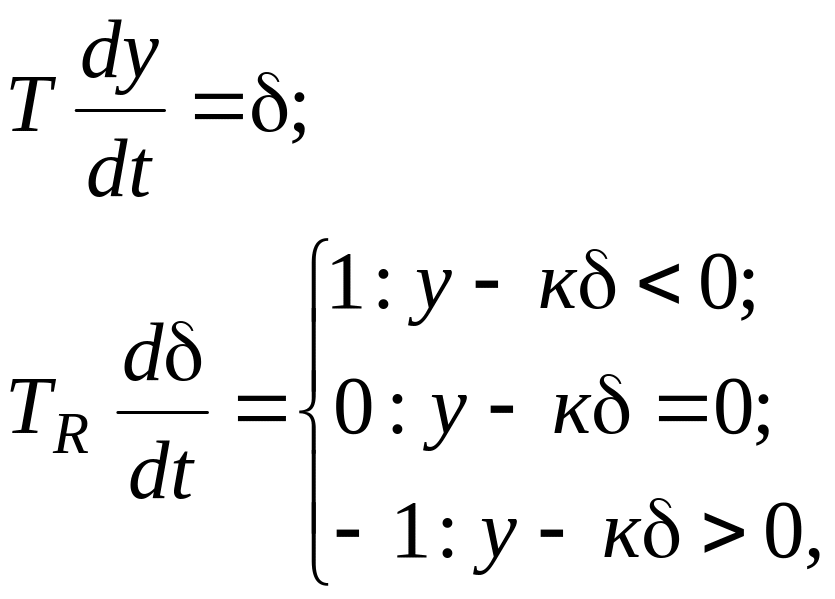(5.19)

где введено обозначение .

При будет справедливо одно уравнение исполнительного привода, при – другое, что следует учесть при построении кривой переходного процесса.

Интегрируя уравнение исполнительного привода, имеем (рис. 5.10):

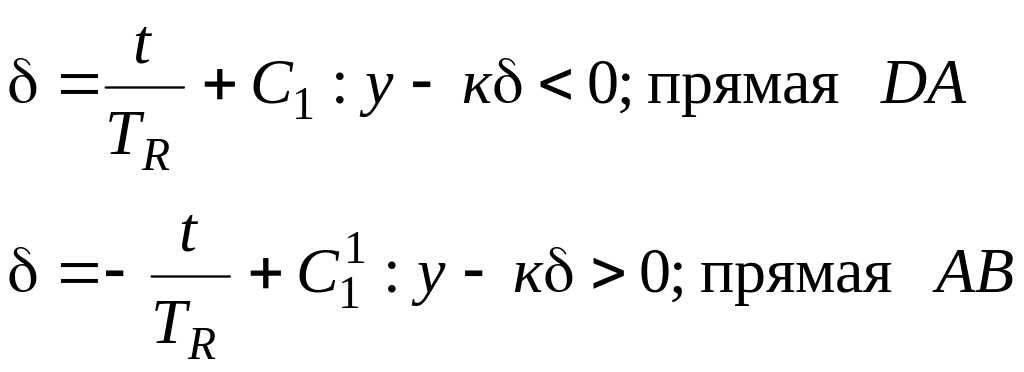(5.20)

где – произвольные постоянные, определяемые начальными условиями. Подставляя значения  из (5.20) в уравнение пл и интегрируя последнее, получаем (рис. 5.10):

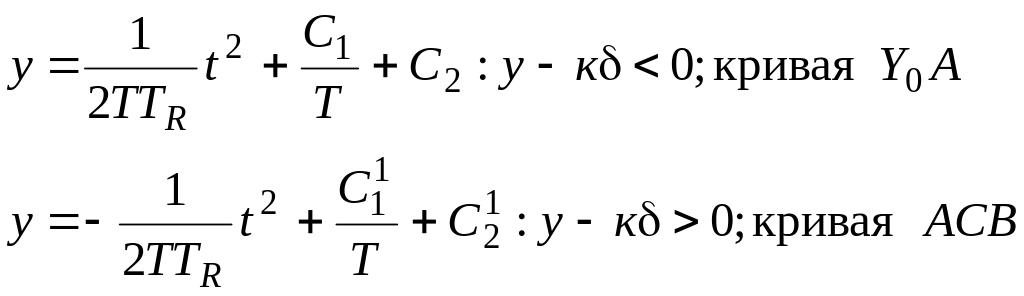(5.21)

где – новые произвольные постоянные, соответствующие и .

Уравнения (5.20) и (5.21) и есть уравнения переходного процесса. При изменении знака суммы происходит изменение знака скорости. Этому соответствует переход к уравнениям со знаком ( – ) в (5.20 и 5.21) или обратно.

Другой пример построения переходного процесса в релейной САР методом припасовывания покажем для системы стабилизации давления газа в расходном баллоне, схема которой представлена на рис. 5.11.

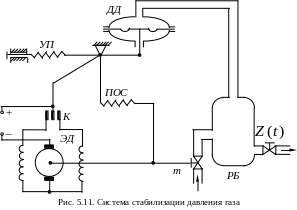
Объектом регулирования здесь является расходный баллон газа РБ, регулируемым параметром – давление газа Р, которое должно быть постоянным, регулирующим органом – клапан m подвода газа к баллону. Приводным двигателем служит реверсивный двигатель постоянного тока ЭД, задающим устройством – установочная пружина УП, натяг которой соответствует заданному давлению. Фактическое давление в баллоне измеряется датчиком давления мембранного типа ДД. При равенстве заданного и фактического давлений контактная группа К разомкнута, электродвигатель стоит. Если равновесие нарушается, контактная группа К включает питание одной из обмоток ЭД, двигатель, вращаясь, перемещает регулирующий клапан m, одновременно выключая контакты через пружину обратной связи ПОС. Возмущающим воздействием для рассматриваемой САР стабилизации давления будет расход газа .

С учетом сказанного, уравнение объекта запишется в виде:

(5.22)

где – постоянная времени баллона, – регулируемый параметр, – регулирующее воздействие.

Координата контактной группы является функцией регулируемого параметра , измеряемой датчиком давления, и регулирующего воздействия , реализуемого через обратную связь. Поэтому можно записать:

(5.23)

где и – коэффициенты усиления.

Приводной двигатель вращается с постоянной скоростью, его уравнение можно записать в виде:

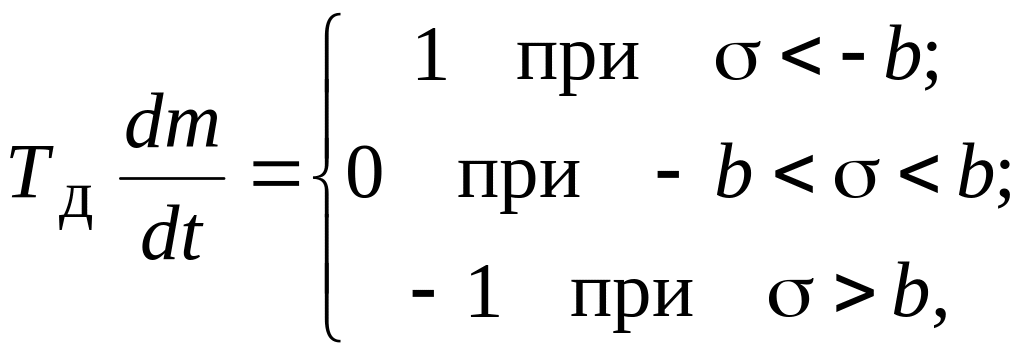(5.24)

где – постоянная времени двигателя, – половина ширины его мертвой зоны.

Рассмотренная система с уравнениями (5.22) – (5.24) является релейной системой.

Положим , считая отличным от нуля начальные условия. Пренебрегаем мертвой зоной двигателя ввиду ее малости, т.е. . Заметим, что при условие равносильно условию , а условие – условию . С учетом этого система уравнений (5.22) – (5.24) запишется в виде

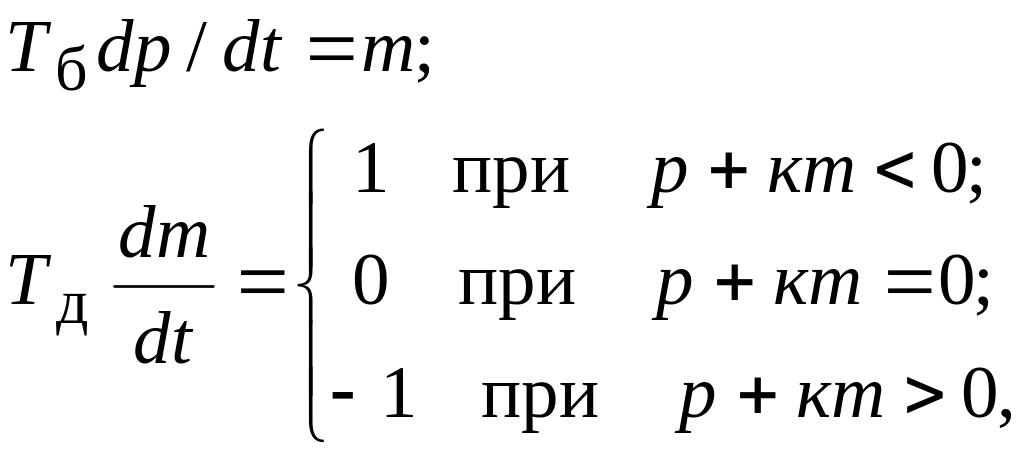(5.25)

где

При будет справедливо одно уравнение двигателя, при – другое, что следует учитывать при построении кривой переходного процесса. Интегрируя уравнение двигателя, получим

(5.26 а)

(5.26 б)

где – постоянные, определяемые начальными условиями.

Подставляя значения из (5.26 а и б) в уравнение объекта (5.22) и интегрируя его, будем иметь

(5.27 а)

(5.27 б)

где – новые произвольные постоянные.

Уравнения (5.27 а и б) и есть уравнения переходного процесса. При изменении знака суммы происходит переключение контактной группы, скорость двигателя меняет знак. Этому соответствует переход от уравнений (5.26 а), (5.27 а) к уравнениям (5.26 б), (5.27 б) или обратно.

Начальное движение системы определяется знаком суммы , заданным начальными условиями. Пусть при имеем

т.е.

Тогда движение описывается уравнениями (5.26 а) и (5.27 а) или, если определить из этих уравнений произвольные постоянные по заданным начальным условиям, уравнениями:

(5.28)

Это движение продолжается до тех пор, пока не изменится знак суммы . Из уравнений (5.28) имеем

(5.29)

В некоторый момент времени получим , тогда произойдет смена уравнений движения. Значение найдем согласно выражению (5.29) из алгебраического уравнения

(5.30)

Из двух значений , которые являются решением уравнения (5.30), выберем подходящее по физическому смыслу (оно должно быть положительным). После этого по формулам (5.28) определяем величины и в конце первого этапа переходного процесса, соответствующего неравенству :

Теперь переходный процесс будет описываться уравнениями (5.26 б), (5.27 б), соответствующими значению , в которых следует определить произвольные постоянные. На втором этапе переходного процесса удобно снова вести отсчет времени от нуля. Начальные значения функций и для второго этапа будут равны, ввиду непрерывности этих функций их конечным значениям на первом этапе переходного процесса. Поэтому для второго этапа процесса начальными условиями будут: . Подставляя их в уравнение (5.26 б) и (5.27 б) и полагая , находим значения произвольных постоянных: . Значит, для второго этапа переходного процесса уравнения (5.26 б) и (5.27 б) запишутся так:

(5.31)

Из выражения (5.31) находим

Приравняв последнее выражение нулю, можно найти , при котором вновь произойдет переключение контактной группы. Тогда по формуле (5.31) получим значения и в конце второго этапа переходного процесса:

Эти значения будут начальными условиями для третьего этапа переходного процесса, на котором движение снова будет описываться теми же уравнениями, что и на первом этапе, но с другими значениями произвольных постоянных и и т.д.

График переходного процесса показан на рис. 5.12.

На этом графике удобно откладывать значения функций и , т.к. при условии , когда пересекаются две кривые, происходит переключение контактной группы и смена уравнений. На участке 0–1 координата , согласно выражению (5.28), изменяется по параболе, осью симметрии которой служит ось ординат. Вершина параболы обращена вниз, т.к. . Координата на этом участке возрастает по прямой, следовательно, убывает также по прямой. В момент имеем ; далее меняется по параболе (5.31), ось симметрии которой параллельна оси ординат, а вершина обращена вверх, т.к. . Координата , согласно формуле (5.31), на участке 1–2 убывает, значит, переменная возрастает. Отклонения и постепенно уменьшаются, значит САР устойчива.

В рассмотренных примерах нелинейная характеристика ЭД состоит из двух отрезков прямых. Поэтому система нелинейных уравнений распадается на две линейные системы, каждая из которых справедлива в определенной области значений переменных. Если нелинейная характеристика системы составлена из отрезков прямых, то система называется кусочно-линейной. Движение кусочно-линейной системы может быть описано решениями ряда последовательно сменяющих друг друга систем линейных дифференциальных уравнений. При этом конечные значения переменных предыдущих участков принимаются за начальные значения переменных последующих участков. Такой метод построения переходных процессов в нелинейных системах называется методом припасовывания, так как он предполагает определение постоянных интегрирования исходя из согласования (припасовывания) значений переменных на границе соседних участков. Построив методом припасовывания кривую переходного процесса и проанализировав ее, можно определить условия устойчивости системы, а также оценить качество переходного процесса.

Метод припасовывания применяется для построения переходных процессов как в релейных, так и в других более сложных кусочно-линейных системах. Недостатком метода является его громоздкость, поэтому он редко применяется в инженерной практике.

5.3.2. Скользящие режимы в релейных САУ. Выше при построении переходного процесса в первом примере предполагалось, что каждые две соседние точки пересечения прямой – к(t), которую будем называть прямой исполнительного привода АВ, с кривой y(t) – параболой объекта управления – лежат по разные стороны от вершины параболы (С). Если прямая двигателя располагается достаточно круто по отношению к оси времени, то после некоторого числа колебаний может оказаться, что две соседние точки пересечения этой прямой с параболой объекта управления будут лежать по одну сторону от вершины параболы. Такой случай изображен на рис. 5.13, где точки А и В лежат по одну сторону от вершины параболы – точки С. Из графика переходного процесса нетрудно видеть, что если кривая y(t) располагается на графике выше прямой исполнительного привода (ИП), то знак суммы положителен, и наоборот, если парабола объекта расположена ниже прямой – к(t), знак данной суммы обязательно отрицателен. Положительному знаку суммы согласно уравнению (5.19) соответствует отрицательная скорость ИП, и наоборот, если , то . Между точками А и В парабола объекта управления (ОУ) проходит выше прямой ИП, здесь , скорость ИП отрицательна. Как будет происходить движение после встречи кривых в точке В, для которой ? В этой точке возникают особые, вытекающие из расположения кривых, условия, которых нет в предыдущих точках пересечения А, F и др. Допустим, что скорость привода в точке В изменится и станет положительной, т.е. прямая ИП пойдет в направлении ВD. Но тогда сразу же после момента переключения парабола ОУ пойдет выше прямой ИП, т.е. будет и, следовательно, как и на участке АВ, скорость ИП должна быть отрицательной, а значит, прямая ИП должна идти в направлении линии ВЕ.

Допустим теперь, что прямая ИП после точки В идет в направлении линии ВЕ, т.е. скорость ИП отрицательна. Но тогда сразу же после момента прохождения точки В парабола объекта располагается ниже прямой ИП, т.е. получаем , и, следовательно, скорость двигателя должна стать положительной, а прямая ИП должна пойти в направлении линии ВD. Стоит только предположить движение в направлении ВD (ниже параболы объекта), как возникают условия, при которых движение должно совершаться в направлении ВЕ. Наоборот, как только мы допускаем движение в направлении ВЕ (выше параболы объекта), так возникают условия, при которых движение может совершаться только в направлении ВD. Поэтому кривая – к(t) после точки В не может идти ни выше, ни ниже кривой y(t), она может только совпадать с этой кривой:

(5.32)

Уравнение (5.32) можно получить, если принять, что скорость ИП с бесконечно большой частотой меняет знак, при этом средняя скорость .

Согласно уравнению (5.32), кривая ИП следит за кривой ОУ, «скользит» по ней, поэтому такой режим работы релейных САУ называется скользящим режимом.

Если увеличить угловой коэффициент прямой АЕ (рис. 5.13), то точка В будет приближаться к точке А и в пределе сольется с ней. В последнем случае скользящий режим работы будет начинаться сразу от точки А. При соответствующих условиях переходный процесс целиком, с самого начала, может протекать в скользящем режиме.

В данной точке графика переходного процесса скользящий режим возникает, если прямая ИП идет круче кривой объекта, т.е. условие возникновения скользящего режима имеет вид

(5.33)

и определяется как параметрами системы, так и начальными условиями. Объединяя уравнение (5.32), представляющее собой уравнение ИП после точки В, с уравнением ОУ, имеем

, (5.34)

откуда

, (5.35)

где при , т.е. . Таким образом, движение релейной системы в скользящем режиме описывается решением линейного дифференциального уравнения.

Чтобы разобраться в причинах возникновения скользящего режима, заменим в рассматриваемой задаче идеальную релейную характеристику реальной характеристикой с мертвой зоной и гистерезисными петлями, рис. 5.14. Рассмотрим, как может изменяться скорость ИП под воздействием входной координаты . Значение отклонения согласно (5.17) определяется значениями регулируемой величины и воздействия обратной связи . Допустим, что за счет изменения значение достигло значения, соответствующего абсциссе точки а на рис. 5.14.

Тогда ИП включится и обратная связь будет стремиться возвратить в среднее положение. Если действие этой обратной связи будет достаточно эффективным, то координата уменьшится настолько, что станет меньше абсциссы точки d, рис. 5.14, и в момент прохождения точки d ИП остановится. Одновременно с остановкой ИП воздействие обратной связи перестанет изменяться, и, если отклонение по-прежнему нарастает в ту же сторону, координата снова увеличится, достигнув абсциссы точки а, ИП снова включится в ту же сторону. Но включение ИП опять приведет в действие обратную связь, стремящуюся снова уменьшить , и т.д.

Таким образом, будет происходить обход по петле abcd релейной характеристики, сопровождающейся частыми включениями и выключениями ИП. Это движение реальной системы будет аналогом скользящего режима в системе с идеальной характеристикой, но при наличии мертвой зоны и гистерезиса координата  следит за координатой не точно, а с некоторым отставанием. При этом сумма , а равна некоторой величине, определяемой абсциссами точек a и d на рис. 5.14. Если ширину гистерезисной петли устремить к нулю, то в пределе получим скользящий режим для идеализированной системы, в которой включения и выключения ИП происходят мгновенно и с бесконечно большой частотой.

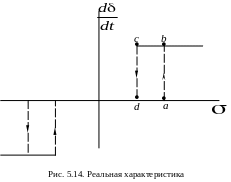
Из сказанного выше следует, что скользящие режимы характерны для релейных систем, у которых релейный элемент охвачен обратной связью. Чем эффективнее действие обратной связи, т.е. чем больше коэффициент обратной связи , тем круче расположена на графике переходного процесса прямая ИП и тем вероятнее возникновение скользящего режима.

Можно сделать следующий вывод: скользящие режимы являются идеализацией реальных ИП особого вида, они возникают ввиду наличия разрывов непрерывности у идеализированных нелинейных характеристик.