5.4. Фазовое пространство

5.4.1. Фазовое пространство, изображение процессов на фазовой плоскости. Для наглядного представления о сложных нелинейных процессах управления часто прибегают к понятию фазового пространства, которое заключается в следующем.

Дифференциальное уравнение замкнутой САУ n-ого порядка можно преобразовать к системе n дифференциальных уравнений первого порядка (в форме Коши) в виде

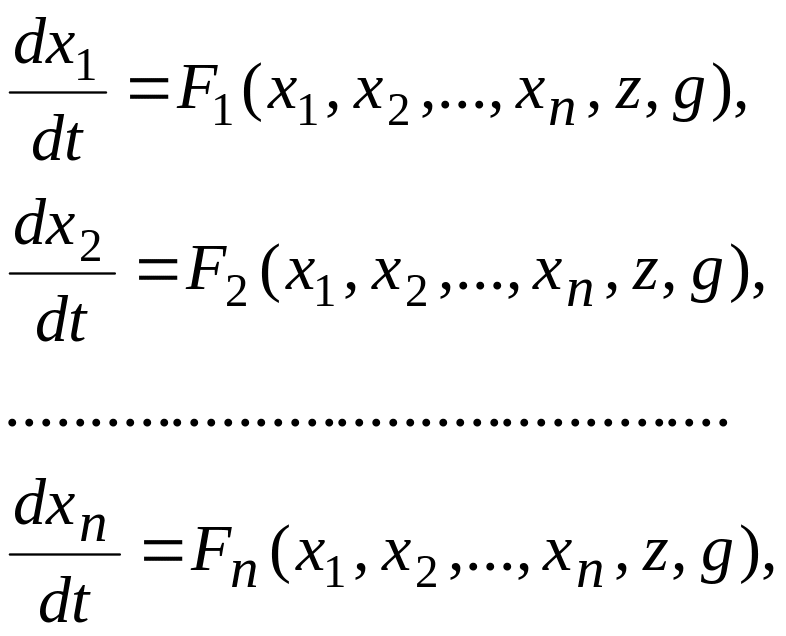(5.36)

с начальными условиями

при ,

где – переменные, являющиеся искомыми функциями времени, причем может обозначать регулируемую величину, а – вспомогательные переменные; и – возмущающие и задающие воздействия. Рассмотрим приведение дифференциальных уравнений к подобному виду на примере дифференциального уравнения второго порядка.

Пусть САУ описывается дифференциальным уравнением вида

(5.37)

где – постоянные коэффициенты, F – некоторая нелинейная функция.

Обозначая , вместо уравнения (5.37) получим систему уравнений

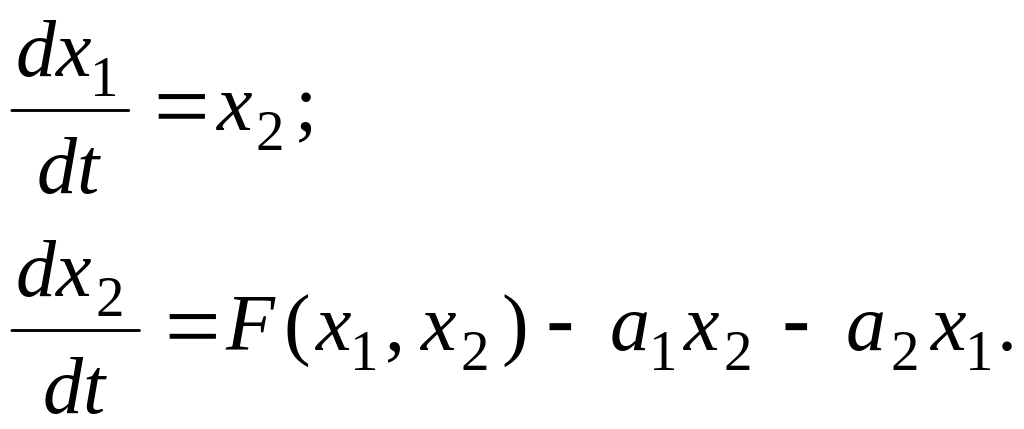(5.38)

Разделим второе уравнение (5.38) на первое, тогда

. (5.39)

Решение уравнения (5.39), образованного из уравнения (5.37), будет служить решением и для исходного уравнения (5.37). Но в уравнении (5.39) исключено время , поэтому его решение представит зависимость между текущими значениями координаты и производной от этой координаты по времени . Вид общего интеграла уравнения (5.39) будет зависеть от конкретного вида функции . В общем случае этот интеграл можно записать так

, (5.40)

где – некоторая функция; C - постоянная интегрирования.

Уравнению (5.40) соответствует семейство кривых на плоскости – интегральных кривых уравнения (5.39). Эти кривые будут служить траекториями движения изображающей точки на плоскости . Такие траектории принято называть фазовыми траекториями, а плоскость, на которую они наносятся, – фазовой плоскостью или плоскостью состояний (фаза – величина, характеризующая состояние колеблющейся системы в данное мгновение; каждая точка рассматриваемой плоскости соответствует определенному состоянию системы, в связи с чем эта плоскость и называется фазовой).

В равновесном статическом режиме имеем , или согласно выражению (5.38)

(5.41)

т.е. числитель и знаменатель правой части уравнения (5.38) обращаются в нули. При этом величина , определяющая направление касательной к фазовым траекториям, становится неопределенной. Точки фазовой плоскости, в которой , называются особыми точками. В рассматриваемом случае координаты особых точек определяются решением системы (5.41). В частном случае система (5.41) может иметь решение

(5.42)

в более общем случае, например, решение

(5.43)

Таким образом, статические режимы изображаются особыми точками, располагающимися обычно у начала координат фазовой плоскости. Если имеется изолированная особая точка с координатами (5.42), она называется точкой покоя. Если имеется множество особых точек с координатами (5.43), определяющими на фазовой плоскости некоторый отрезок, то последний называется отрезком покоя.

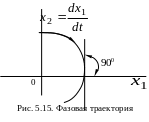
Рассмотрим, как движется по фазовым траекториям изображающая точка. При координата возрастает, при – убывает. Следовательно, при расположении координатных осей, принятом на рис. 5.15, изображающая точка будет двигаться, вращаясь вокруг начала координат фазовой плоскости по часовой стрелке. При фазовые траектории пересекают ось под прямым углом, так как в этих точках координата имеет экстремум.

Характер фазовых траекторий определяется видом исходного уравнения, начальное положение изображающей точки на фазовой плоскости определяется начальными условиями. Фазовая плоскость с траекториями в целом соответствует общему решению системы и характеризует совокупность всех возможных движений. Та или иная фазовая траектория в отдельности соответствует частному решению и характеризует данное конкретное движение.

Построив фазовые траектории, всегда можно проследить, как движется по ним изображающая точка относительно точки или отрезка покоя.

Если изображающая точка с течением времени неограниченно удаляется от точки покоя, соответствующее равновесное состояние неустойчиво.

Наоборот, если изображающая точка, независимо от ее начального положения, двигаясь по фазовым траекториям, приходит к точке покоя, состояние равновесия устойчиво.

Итак, совокупность фазовых траекторий на плоскости определяет все возможные движения системы и служит наглядным изображением ее динамических свойств. Поэтому фазовую плоскость с нанесенными на нее траекториями называют фазовым портретом системы.

Система второго порядка имеет две независимые переменные и . Поэтому фазовый портрет системы (5.38) изображается на плоскости, имеющей две координатные оси. Если система дифференциальных уравнений имеет третий порядок, то фазовые траектории размещаются в трехмерном фазовом пространстве. В случае системы уравнений n–ого порядка (5.36) фазовое пространство имеет n измерений.

Геометрические построения в пространстве значительно менее наглядны, нежели геометрические построения на плоскости. Поэтому наибольшее практическое применение имеют методы построения фазовых траекторий на плоскости, когда система имеет второй порядок. Тем не менее, понятие фазового пространства, или пространства состояний, является фундаментальным для теории нелинейных систем при любом порядке исходных уравнений.

5.4.2. Фазовые траектории линейной системы второго порядка. Типы особых точек. Пусть система описывается линейным дифференциальным уравнением второго порядка с постоянными коэффициентами

(5.44)

Обозначая, как и выше,

, (5.45)

из уравнения (5.44) имеем

. (5.46)

Разделив уравнение (5.46) на (5.45), получим

. (5.47)

Согласно выражению (5.47), на фазовой плоскости имеется точка покоя с координатами .

Сделаем в уравнении (5.47) замену переменных

. (5.48)

Дифференцируя это выражение, имеем

. (5.49)

Подставляя выражения (5.49) и (5.48) в (5.47), получаем уравнение с разделяющими переменными

(5.50)

Разлагая знаменатель левой части на множители, находим

(5.51)

где и – корни характеристического уравнения

. (5.52)

В уравнении (5.51) заменим на , тогда получим уравнение семейства фазовых траекторий, вид которых будет зависеть от типа корней и .

Пусть корни чисто мнимые: и . Тогда переходный процесс изображается синусоидой, рис. 5.16 а, амплитуда и начальная фаза которой определяются начальными условиями. Уравнение 5.51 принимает вид

. (5.53)

Интегрируя это уравнение, находим

. (5.54)

Обозначая и учитывая выражение (5.48), из уравнения (5.54) получаем уравнение семейства эллипсов

(5.55)

с полуосями и . Следовательно, фазовые траектории представляют собой семейство замкнутых кривых, вложенных одна в другую, рис. 5.16 б. Особая точка типа начала координат фазового портрета называется центром.

x₁

Пусть и – комплексные корни с отрицательными вещественными частями. В таком случае переходный процесс будет затухающим колебательным, рис. 5.17 а. Если уже имеется график этого процесса, то фазовую траекторию можно построить и не прибегая к интегрированию уравнений. В рассматриваемом случае для этого достаточно снять с графика процесса соответствующие друг другу значения , где  – угол наклона касательной к кривой. На участке ОА функция возрастает, здесь . Этому соответствует участок ОА фазовой траектории на рис. 5.17 б. В точке А координата достигает максимума, здесь производная обращается в нуль и т.п. Как видим, затухающему колебательному процессу соответствует фазовая траектория в виде спирали, наматывающейся на начало координат. Особая точка, на которую наматываются спиралями все расположенные в ее окрестности траектории, называется устойчивым фокусом.

Пусть корни уравнения (5.52) – комплексные с положительными вещественными частями. Тогда процесс будет колебательным расходящимся, фазовая траектория будет иметь вид спирали, разматывающейся от начала координат, рис. 5.18. Особая точка, соответствующая этому случаю, называется неустойчивым фокусом.

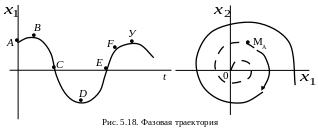
x₁

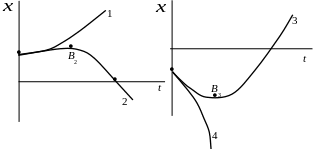
Пусть корни уравнения (5.52) – вещественные отрицательные. В этом случае процесс будет монотонным (кривая 2,5 на рис. 5.19 а, б, с перерегулированием (кривая 1,4) или промежуточной формы (кривая 3,6). Монотонному процессу на фазовой плоскости соответствует траектория, вливающаяся в начало координат, при движении вдоль которой все время уменьшается (кривая 2,5 на рис. 5.19 в). Процессу с перерегулированием соответствует вливающаяся в начало координат траектория, при движении вдоль которой меняет знак (кривая 1,4). Процессу промежуточной формы соответствует траектория, при движении вдоль которой знака не меняет, но меняет знак (кривая 3,6). Во всех случаях функция лишь в пределе, при , обращается в нуль, поэтому и изображающая точка попадает в начало координат лишь при . Особая точка такого типа называется устойчивым узлом.

Если корни уравнения (5.52) вещественные положительные, то переходный процесс будет апериодическим расходящимся, рис. 5.20 а,б. Этому процессу соответствует фазовая траектория, выходящая от начала координат и удаляющаяся в бесконечность, рис. 5.20 в. Начало координат фазовой плоскости представляет здесь особую точку, называемую неустойчивым узлом.

Пусть, наконец, уравнение имеет вещественные корни разных знаков. В этом случае особая точка называется седлом. В нее входят две и из нее выходят две траектории, остальные траектории с ней не касаются, рис. 5.21.