2. Многомодовость нечеткого множества.

Многомодовость нечеткого множества обуславливается данными, имеющими «сгустки» распределения уверенности. Например, в оценках типа (Рис. 1.6):

«Может быть 10, а может быть и 15, но с меньшей степенью уверенности»

При обработки подобных данных возникают неоднозначности решений, что затрудняет как алгоритмизацию вычислительных процедур, так и интерпретацию получаемых решений.

• Вариантами решения проблемы является:

1. Разбитие многомодового нечеткого множества на отдельные моды (Рис. 1.6);

2. Построение «выпуклой оболочки» многомодового нечеткого множества (Рис. 1.6);

3. Использование полученного результата с учетом его многомодовости.

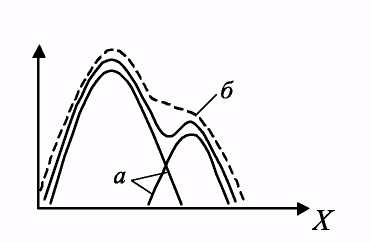
Рисунок 1.6 — Представление многомодового нечеткого множества

3. Ошибка центра масс нечеткого множества

Трудность обусловлена тем, что при смещении мало значащих значений в сторону больших значений X (рис. 17, при упорядоченном X, в частности при использовании нечетких чисел) наблюдается смещение центра масс нечеткого множества, что приводит к ошибкам интерпретации значения нечеткого множества.

Рисунок 1.7 — Пример смещения центра масс при учете малозначащих значений

Возможным вариантом устранения погрешностей является использование подходов α-уровневой фильтрации («отсечение» значений с функцией принадлежности меньше α, см. рис. 1.7).

4. Сложности определения нечеткого множества для сложных понятий

Проблема обусловлена возникновением естественных трудностей для специалиста, который должен определить нечеткие оценки для сложного понятия. Данные трудности связаны с трудностями психологического шкалирования.

Операции над нечеткими множествами

В настоящее время разработано достаточно большое количество операций над нечеткими множествами. Ниже в таблице приведены ссылки на основные, наиболее часто используемые операции над нечеткими множествами.

Таблица 3 - Наиболее часто используемые операции над нечеткими множествами.

№	Наименование операции	Интерпретация	Возможные трудности
1	Операция объединения	Операция «ИЛИ». Надо чтобы выполнялось хотя бы одно условие	Появление многомодовости получаемых результатов
2	Операция пересечения	Операция «И». Надо чтобы выполнялись все условия	Уменьшение максимального значения max и появление не нормированных нечетких множеств
3	Операция Сжатия-растяжения	Уточнение, проявление уровня уверенности в оценках.	Необходимо учитывать нелинейный характер преобразований.
4	Импликация (эквивалентн ость)	Операция следования или связи на уровне сравнения объектов	При решении практических задач требует выбора конкретного типа данной операции в соответствии с физикой моделируемого объекта
5	Операция отрицания	Оценка противоположного события.	Зависит от выбранного генератора отрицания и требует выбора конкретного типа отрицания в соответствии с физикой моделируемого объекта
6	┴иТ- нормы и конормы, Средние, OWA-оператор	Могут выполнять различную логику обработки данных в зависимости от выбранных параметров операторов	При решении практических задач требует выбора конкретного типа данной операции в соответствии с физикой моделируемого объекта

Проблема определения операции агрегирования нечетких множеств определяется теми же проблемами, которые отмечены Для получения адекватных оценок необходимо осуществлять процедуры идентификации операций над нечеткими множествами для реальных моделируемых процессов.

Рассмотрим индекс нечеткости или показатель размытости нечетких множеств.

Если объект х обладает свойством R (порождающим нечеткое множество A) лишь в частной мере, т.е. 0<_A(x)<1, то внутренняя неопределенность, двусмысленность объекта х в отношении R проявляется в том, что он, хотя и в разной степени, принадлежит сразу двум противоположным классам: классу объектов, "обладающих свойством R", и классу объектов, "не обладающих свойством R". Эта двусмысленность максимальна, когда степени принадлежности объекта обеим классам равны, т.е. _A(x) = (x)=0,5, и минимальна, когда объект принадлежит только одному классу, т.е. либо _A(x) = 1 и (x) = 0, либо _A(x) = 0 и (x) = 1.

В общем случае показатель размытости нечеткого множества можно определить в виде функционала d(A) со значениями в R (положительная полуось), удовлетворяющего условиям:

1. d(A) = 0 тогда и только тогда, когда А - обычное множество;

2. d(A) максимально тогда и только тогда, когда _A(x) = 0.5 для всех xE.

3. d(A)d(B), если A является заострением B, т.е.

4. _A(x)_B(x) при _B(x) < 0,5;

5. _A(x)_B(x) при _B(x) > 0,5;

6. _A(x)- любое при _B(x) = 0,5.

7. d(A) = d( 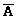) - симметричность по отношению к 0,5.

8. d(AB)+d(AB) = d(A)+d(B).

Обычное множество, ближайшее к нечеткому

Пусть A - нечеткое множество. Возникает вопрос, какое множество AE является ближайшим к A, т.е. находится на наименьшем евклидовом расстоянии от нечеткого множества A. Таким подмножеством, обозначаемым A, является подмножеством с характеристической функцией:

. (1.6)

Обычно принимают _A(x_i) = 0, если _A(x_i) = 0,5.

Используя понятие обычного множества, ближайшего к нечеткому, введем следующие индексы нечеткости нечеткого множества А.

Линейный индекс нечеткости:

Здесь (A, A) - линейное (хеммингово) расстояние, множитель - обеспечивает выполнение условия 0<d(A)<1.

Квадратичный индекс нечеткости

,0<d(A)<1.

Здесь (A, A) - квадратичное (евклидово) расстояние.

Замечания.

1. Мы ввели линейный и квадратичный индексы нечеткости, используя понятие расстояния и понятие обычного множества, ближайшего к нечеткому. Эти же индексы можно определить, используя операцию дополнения, следующим образом:

- линейный индекс,

- квадратичный индекс.

2. Отметим следующие свойства, связанные с ближайшим обычным множеством: АВ=АВ, АВ=АВ;

а также xE:|_A(x_i)-_A(x_i)|=, откуда для линейного индекса нечеткости имеем:

,

т .е. в этом представлении становится очевидным, что d(A)=d( ).

3 . Нечеткое множество с функцией принадлежности иногда называют векторным индикатором нечеткости

Рассмотрев общематематическое понятие «множество» и ряд понятий, с ним связанных, перейдем к его непосредственному применению в сфере безопасности.

Основой образования и результатом распада систем являются множества, представляющие собой совокупность элементов (объектов или субъектов) некоторой общности (находящихся в некоторых отношениях).

Итак, пусть имеется некоторое множество А

а_i A = {a_i}, i=1(1)N,

состоящее из N элементов a_i(R_i,W_i), каждый из которых имеет свой ресурс R_i и свою цель W_i. Допустим, что это самая насущная цель – безопасность, тогда жизнестойкость (вероятность выживания) множества независимых элементов будет определяться

P(W) = P(W₁)P(W₂)…P(W_N) = (1.7)

произведением вероятностей достижения данной цели для каждого элемента.

При этом вероятность – математическая числовая характеристика степени возможности появления какого-либо случайного события.

Вероятность - фундаментальное понятие теории вероятностей, науки, изучающей математические модели случайных явлений (событий).

Существуют различные определения вероятности: философское, интуитивное, статистическое, аксиоматическое и др. Однако ни одно из них не дает исчерпывающего определения реального содержания понятия вероятности, являясь лишь приближе­ниями ко все более полному его раскрытию.

Математическая вероятность - это числовая характеристика степени возможности появления какого-либо определенного явления при определенных, могущих повторяться неограниченное число раз условиях.

Численное значение вероятности в некоторых случаях получается как отношение числа случаев «благоприятствующих» данному явлению, к общему числу «равновозможных» случаев.

В более сложных случаях определение численного значения вероятности требует так называемого статистического подхода, в соответствии с которым под вероятностью события А понимается

Р(А) = m/n ,

где m - число появлений события А; n – общее число опытов; если при

п → ∞ (m/и) → const, т.е. выполняется закон больших чисел (теорема Бернулли).

Поясним суть этого определения с помощью следующего примера.

Предположим, что мы хотим оценить удачность некоторой атаки. Если, сделав 100 выстрелов, в 39 случаях атака удалась, то вероятность р реализации атаки приближенно равна 0,4. Отношение числа случаев т, в которых данное событие появилось, к общему числу испытаний и, так называемая частота т/п, дает приближение к вероятности р, тем лучше, чем больше п.

В рассмотренном примере m =39, n = 100. В то же время, если из пяти первых атак две реализованы, то мы сильно рискуем ошибиться, утверждая, что 40% атак окажутся удачными.

По вероятности, вычисленной статистическим способом, т.е. приближенно, могут быть вычислены по правилам теории вероятностей новые вероятности.

Например, для ранее рассмотренного примера с атаками вероятность того, что хотя бы один из двух будет реализована равна 1 – (1 – 0,4)2 = 0,64.

Для многих практических применений статистическое определение вероятности оказывается вполне достаточным. Из определения вероятности как частоты следует, что вероятность р любого события есть некоторое постоянное число, удовлетворяющее условию 0 <р< 1.

Важное значение статистического определения заключается в том, что оно дает нам принцип физического выбора величины вероятности и требует учитывать данные опыта.

Логически непротиворечивым математическим определением вероятности является аксиоматическое определение, которое устраняет некоторую неопределенность статистического определения.

В общем случае вероятность р, может иметь более широкую трактовку и использоваться не в строгом смысле, принятом в теории вероятностей, справедливом для стохастических, повторяющихся явлений, а характеризовать единичные явления, события, появление которых нельзя предсказать на основе представительной выборки.

В условии взаимозависимости элементов жизнестойкость их совокупности будет определяться

P(W) = P(W₁)P(W₂/W₁)P(W₃/W₁∩W₂)…P(W_N/ ) (1.8)

произведением условных вероятностей достижения цели для k-го элемента при условии совместного достижения целей для всех элементов от 1 до (k-1), т.е.

P(W)= , (1.9)

где условная вероятность – вероятность одного события при условии совершения другого события.

Отсюда, мотив образования системы, прежде всего, состоит в том, что для большинства k имеет место неравенство (1.10)

>P(W_k), (1.10)

т.е. для k-го элемента вероятность достижения его цели W_k выше в случае достижения целей других (k-1) элементов. Элементы способствуют друг другу в достижении своих целей. Очевидно жизнестойкость их совокупности (при наличии устойчивых связей это уже прообраз системы) в целом также повышается (1.8) в сравнении с вариантом (1.7) взаимной независимости элементов.

С другой стороны, обратное неравенство (1.11)

<P(W_k) (1.11)

является мотивом для распада системы. В этом случае элементы своими взаимосвязями (1.8) осложняют друг другу достижение своих целей (конфликтность целей).

Условная вероятность (1.9) свидетельствует о наличии связей между элементами. Их характер: негативный (конфликтность целей элементов) или позитивный (союзность целей элементов) мотивирует распад (1.11) или образование (1.10) систем (на рассматриваемом множестве элементов).