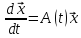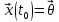Шпоры.Диффуры.3 сем
.docx
|
20. ФСР однородного ЛДУ с постоянными коэффициентами в случае, когда характеристическое уравнение имеет кратные корни. L[y]=y^{n}+a1y^{n-1}+…+a(n-1)y’+an*y=0 (13) l(t)=t^n+a1t^(n-1)+…+a(n-1)t+an (15) Определение Говорят, что число C является корнем кратности k многочлена l(t) степени (n-k), если l(t)=(t-)^k*l1(t), где l1()0. Если k=1, - простой корень. L=l(D)=D^n+a1*D^(n-1)+…+a(n-1)*D+an. Пусть - корень кратности k l(t), т.е. l(t)=(t-)^k*l1(t), то L=l(D)=(D-)^k*l1(D)=l1(D)*(D-)^k .Зафиксируем sN s=0 (натуральные и ноль) x^s*e^x, (D-)^k*[x^s*e^x] 1. k=1 (D-)^k*[x^s*e^x]==(det) D*[x^s*e^x]-*[x^s*e^x]= =(d/dx)*[x^s*e^x]-*[x^s*e^x]= =s*x^(s-1)*e^x+*[x^s*e^x]-*[x^s*e^x]=s*[x^(s-1)*e^x] (D-)*[x^s*e^x]=[s*[x^(s-1)*e^x], sN; 0, s=0] 2. (D-)^2*[x^s*e^x]= (D-)*[(D-)*[x^s*e^x]]= =(D-)*[s*x^(s-1)*e^x]=s*(D-)*[x^(s-1)*e^x]= =[s*(s-1)*[x^(s-2)*e^x], s>1; 0, 0<=s<=1] kN. (D-)^k*[x^s*e^x]=[k*(k-1)*…*(k-s+1)[x^(s-k)*e^x], s>=k; 0, 0<=s<=k-1] Теорема 1: Пусть C явл. корнем кратности k храк-кого многочлена, тогда функции e^x, x*e^x,..,x^(k-1)*e^x являются решениями (13) Доказательство (13) L[y]=0 L=l[D]=l1(D)* (D-)^k 0<=s<=k-1: L[x^s*e^x]=(l1[D]* (D-)^k)*[x^s*e^x]=l1(D)*( (D-)^k*[x^s*e^x])= l1(D)[0]=0, т.к. 0<=s<=k-1. => x^s*e^x- реш. (13)
|
19. ФСР однородного ЛДУ с постоянными коэффициента-ми в случае простых корней характеристического уравнения (действительных или комплексных). Теорема1: Пусть a1,..,anC и L[y]=y{n}+a1*y{n-1}+…+a(n-1)*y’+an*y=0 (13) и l(t)=t^n+a1*t^(n-1)+…+a(n-1)*t+an (15)– характеристический многочлен ОЛДУ(13). Функция e^x, где C, Является решением (13) т. и т. т., когда l()=0 (т.е. - корень характеристического многочлена (13)) Доказательство Т.к. L[e^x]= D^n*[e^x]+…+ a(n-1)*D*[ e^x ]= e^x*(^n +…+ a(n-1) * + an) = e^x * e()=0 <=> e[]=0 Лемма Пусть 1, 2,.., nC, причем ij при ij. Тогда функции e^1x, e^2x,.., e^nx линейно независимы на R Доказательство: Индукция по n: 1) n=1 1*e^1x=0 <=> 1=0 – утверждение верно 2) Пусть для попарно независ. M1,..,M( n-1)- утверждение верно 3) ij, ij, e^1x, e^2x,.., e^nx . ПустьxR и 1,.., nC 1*e^1x+2*e^2x+…+n* e^nx0 , умножим на e^(-nx) x: 1* e^(1-n)x+…+(n-1)*e^((n-1)-n)x + n0. Дифференцируем (1-n)*1*e^(1-n)x+…+((n-1)-n)*(n-1)*e^((n-1)-n)x0 Т.к.: 1-n…(n-1)-n, то п индуктивному предположению => e^(1-n)x,..,e^((n-1)- n)x – линейно независимы на R Замечание:(i-n)i0, i=1,..,(n-1) => 1=2=…=(n-1)=0 n*e^nx0=> n=0 => e^1x,…, e^nx.
|
17. Теорема об общем решении неоднородного ЛДУ порядка n. (8) y{n}+p1(x)*y{n-1}+…+p(n-1)(x)*y’+pn(x)*y=f(x) (8) L[y]=f(x) – неоднородное ЛДУ (9) y{n}+p1(x)*y{n-1}+…+pny=0 (9) L[y]=0 Говорят, что однородное уравнение (9) соответствует неоднородному уравнению (8) Теорема:Общее решение уравнения (8) представляется как сумма общего решения соотв. Однороднод.ЛДУ (9) и некоторого частного решения yч.н.(x) уравнения (8).Если y1(x),…,yn(x)-ФСР неоднор. ИДУ(9), а yч(x)-частное решение неоднор. ЛДУ(8), то общее решение (8): y(x)=yч.н.+С1*y1(x)+…+Cn*yn(x) (10), где C1,..,Cn – произвольные const. Док-во: Пусть y2(x)-фикс.частное решение ур-ния(8) 1)Пусть φ(x) решение ур-ния(9),т.е. L[φ (x)]=0.Тогда по теореме о размерности пр-ва: φ(x)=C1y1(x)+C2y2(x)+…+Cnyn(x),т.к. y1(x),…,yn(x)-ФСР ур-ния(9).По условию L[yч(x)]=f(x), y(x)=yч(x)+ φ(x)=yч(x)+C1y1(x)+…+Cnyn(x)-решение(8). L[y(x)]=L[yч(x)+ φ(x)]= L[yч(x)]+L[φ(x)]=f(x)+0=f(x) 2)Пусть y(x)-произвольное решение ур-ния(8),т.е. L[y(x)]=f(x),рассмотрим z(x)=y(x)-yч(x), L[z(x)]=L[y(x)]-L[yч(x)]=f(x)-f(x)=0 сл-но z(x)-решение ур-ния(9) сл-но найдутся числа C1,C2,…,Cn такие, что z(x)=C1y1(x)+…+Cnyn(x) и y(x)=yч(x)+C1y1(x)+…+Cnyn(x).
|
|
18.Метод вариации произвольных постоянных для неоднородного ЛДУ порядка n. Пусть найдены y1(x),..,yn(x) – ФСР (9) Будем искать yч.(x) – частное решение неоднородного уравнения (8) в виде: yч.=C1(x)*y1(x)+…+Cn(x)*yn(x), где C1(x),..,Cn(x) – непрерывно дифференцируемые на I функции, подлежащие определению. k=1,..,n L[yk(x)]=0 yч.=(i=1)(n)(Ci(x)yi(x)) При подстановке yч. В (8) получится: y’ч.(x)= (i=1)(n)(Ci(x)*y’i(x))+ (i=1)(n)(C’i(x)*yi(x)) Наложим дополнительные условия (i=1)(n)(C’i(x)*yi(x))=0, тогда y’ч.= (i=1)(n)(Ci(x)*y’i(x)) y’’ч.= (i=1)(n)(Ci(x)*y’’i(x))+ (i=1)(n)(C’i(x)*y’i(x)) (i=1)(n)(C’i(x)*y’i(x))=0 Итак, пусть (i=1)(n)(C’i(x)*y{k}i(x))=0 для k=0,..,n-2 y{n-2}ч.= (i=1)(n)(Ci(x)*y{n-1}i(x)) Решаем неоднородное уравнение L[y]=f(x) y{n}(x)+p1(x)*y{n-1}(x)+…+p(n-1)(x)*y’(x)+pn(x)*y(x)=f(x) Ищем частное решение в виде yч.=(i=1)(n)(Ci(x)*yi(x)), y1(x),..,yn(x) – ФСР L[y]=0 y{k}ч.= (i=1)(n)(Ci(x)*y{k}i(x)), k=1,..,n-1. Получим систему из n ур-ний: (i=1)(n)(C’i(x)*y{k}i(x))=0 y{n}(x)=(i=1)(n)(C’i(x)*y{n-1}i(x))+ (i=1)(n)(Ci(x)*y{n}i(x)). |
21. Отыскание частного решение неоднородного ЛДУ с постоянными коэффициентами и стандартной правой частью. (18) L[y]= y^(n)+any^(n-1)+…+a(n-1)y^(1)+any=f(x), a1, a2,…., an є C; Известно уо.н.=уч.н.+уо.о. (18.1) L[y]=f(x); L[y]=0; Теорема Пусть єC, a1, a2,…., am є C; Pm(x) – многочлен степени m с комплексными коэф-ми. l(t)=t^n+a1t^(n-1)+…+a(n-1)t+an – характеристический многочлен уравнения (18.1) и f(x)=Pm(x)e^x; (19): L[y]=Pm(x)e^x – неоднородное ЛДУ порядка N. Тогда: 1. (нерезонансный случай). Если l()0 (т.е. не является корнем l(t), то уравнение (19) имеет частное решение yч.(x)=Qm(x)e^x, где Qm(x) – многочлен степени m. 2. (резонансный случай). Если - корень кратности x многочлена l(t), то уравнение (19) имеет частное решение вида yч.=(x^k)Qm(x)e^x, где Qm(x) многочлен степени m. Доказательство (случай m=0, т.е. Pm(x)=A, AC; f(x)=Ae^x) 1. L[y]=Ae^x; l()0; yч.=Be^x (В подлежит определению); Подставляем yч.(x) в (19) L[yч.(x)]=L[Be^x]=BL[e^x]=Bl()e^x=f(x)=Ae^x <=> Bl()=A, т.к. l()0, то B=A/l(); yч.=A/l(x)e^x
|
22. Нормальная система ОДУ. Понятие решения и интегральной кривой. Постановка задачи Коши для нормальной системы, формулировка ТСЕ. Пусть функции f1(x,y1,..,yn), f2(x,y1,..,yn),..,fn(x,y1,..,yn) определены в области Rn+1x,y1,..,yn Опеределение Нормальной системой ОДУ порядка N называется система вида: {dy1/dx=f1(x,y1,..,yn); dy2/dx=f2(x,y1,..,yn);…; dyn/dx=fn(x,y1,..,yn)} (1) Замечания 1) x – независимая переменная, y1(x),..,yn(x) – функции от x. 2) число уравнений системы (1) равно числу зависимых переменных y1,..,yn 3) порядок системы (1) равен числу уравнений 4) каждое уравнение содержит только одну производную, правосторонних производных нет. Пусть I=<,>R Говорят, что на I определены функции y1(x),..,yn(x) и y(x)=(y1(x),..,yn(x))T. Вектор-функция y(x)C1(I) (по определению) <=>(det) i=1,.,n: yi(x)C1(I) (C(I)) dy/dx=(dy1/dx,..,dyn/dx)T=y’=(y1`(x),..,yn`(x)) Обозначим fi(x,y1,..,yn)=fi(x,y) Говорят, что Rn+1x,y1,..,yn задана вектор-функция f(x.y)=(f1(x,y),.., fn(x,y))T, если на определены функции f1(x,y),.., fn(x,y) Векторная запись системы (1): dy/dx= f(x.y) (2), y'= f(x,y) Определение
|
|
23. Нормальная система ЛДУ. Скалярная и матричная запись. Формулировка ТСЕ решения задачи Коши для системы ЛДУ. Нормальную систему порядка n дифференциальных уравнений вида dy1/dx=a11(x)y1+… a1n(x)yn+b1(x); …; dyn/dx=an1(x)y1+… ann(x)yn+bn(x) (1). называют линейной системой, здесь функции aij(x) и bi(x) определены и непрерывны на I=<>. dyi/dx=j=1naij(x)yj+bi(x), i n. fi(x,y)= j=1naij(x)yj+bi(x), i,j dfi(x,y)/dyi=aij(x)C(I). Функции fi(x,y) и dfi(x,y)/dyi определены и непрерывны G=xI=<>; -y1;…;-yn}=I*Rn. Задача Коши для линейной системы: начальные условия: x0I, y10…yn0 – произвольные числа, т.е. y0Rn (произвольный вектор). Запишем систему (1) в матричном виде: b(x)=(b1(x)…bn(x))T, A(x) – матрица-функция порядка n. A(x)=||aij||n*n; dy/dx=A(x)y+b(x). A(x), b(x)C(I). Определение. Если b(x)0, то система dy/dx=A(x)y+b(x) (2) называется неоднородной. Если столбец b(x)=0, то система ЛДУ называется однородной и имеет вид dy/dx=A(x)y Th.(ТСЕ для системы ЛДУ). Пусть вектор-функция b(x) и матрица-функция A(x) определены и непрерывны на I=<>, x0I, y10…yn0 – произвольные действительные числа. Тогда задача Коши: dy/dx=A(x)y+b(x), y(x0)=y0 (y0={y10…yn0}) 1. Имеет решение (x), определенная на всем I. 2. Это решение единственно (т.е. если (x) и (x) – решения, удовлетворяющие условию (x0)=(x0), то xI: (x)(x)).
|
24. Свойства решений однородной системы. Определение. Если b(x)0, то система dy/dx=A(x)y называется однородной системой ЛДУ. Введем оператор =d/dx-A(x); y(x)C1(I); [y(x)]= dy/dx-A(x)y; [ y(x)]C(I). Лемма. Оператор - линейный. Доказательство: Для любых y1(x), y2(x)C1(I) и 1,2R; Z[1y1+2y2]=1dy1/dx + 2dy2 - 1A(x)y1-2A(x)y2=1(dy1/dx-A(x)y1)+2(dy2/dx-A(x)y2)= 1Z[y1]+2Z[y2] . Th. 1. Если вектор-функции 1(x)…n(x) решение системы dy/dx=A(x)y (1), то С1…Сn – числа: C11+…+Cnn – тоже решение системы. 2. Если u(x),v(x)C1(I), а действительная функция (x)= u(x)+iv(x) – решение системы (1), то действительные функции u(x) и v(x) – тоже решения системы. Доказательство: 1. y(x) – решение системы (1) тогда и только тогда, когда [y]= 0, т.е. когда y – лежит в ядре оператора . Т.к. ядро - линейное подпространство, то 1(x)…n(x)Rer C11+…+CnnRer и является решением системы (1). 2. [ y(x)]= dy/dx-A(x)y=0. По условию: 0=[u(x)+iv(x)]=[по лемме 1]=[u(x)]+i[v(x)]=0. Т.к. [u(x)] и [v(x)] – действительные вектор-функции, то [u(x)]=0 и [v(x)]=0.
|
|
|
|
19.Теорема2: Пусть a1,..,anC и (13) l(t)=t^n+a1t^(n-1)+…+a(n-1)t+an – характеристический многочлен уравнения (13). Если 1,2,..,nC – корни характеристического многочлена (15) такие, чтоij при ij, то функции e^1x, e^2x,.., e^nx образуют ФСР ур-ния(13) и общее решение им. вид: y(x)=C1e^1x+ C2e^2x+…+ Cn*e^nx (16), где C1,..,Cn – произвольные комплексные постоянные. Доказательство: Т.к. 1,…, n-корни хар.ур.(15), то по теореме 1 :e^1x, e^2x,.., e^nx – решения (13) По Лемме 4, т.к. ij, ij, то e^1x, e^2x,.., e^nx – линейно независимы => e^1x, e^2x,.., e^nx – ФСР (13) И значит, общее решение (13) имеет вид (16) Действительный случай Пусть a1,..,anR (действительные числа). l(t)=t^n+a1t^(n-1)+…+a(n-1)*t+an – многочлен с действительными коэффициентами. Пусть1, 2,.., n (ij, ij)-корни этого многочлена. а) 1, 2,.., nR, тогда ФСР e^1x, e^2x,.., e^nx – действительная функция y(x)=C1e^1x+ C2e^2x+…+ Cn*e^nx, где С1,..,Сn – произвольные действительные числа |
20.Лемма: Для любых различных 1,2,..,sC и k1,k2,..,ksN, тогда система функций {e^1x, x*e^1x,..,x^(k1-1)*e^1x; e^2x, x*e^2x,..,x^(k2-1)*e^2x;…; e^sx, x*e^sx,..,x^(ks-1)*e^sx} линейно независима на R Теорема Пусть различн. числа 1,2,..,sC - корни характеристического многочлена l(t) кратности k1,..,ks соответственно и k1+…+km=n. Тогда обще решение (13) имеет вид y(x)=P1(x)*e^1x+…+Ps(x)*e^sx, где j=1,..,s Pj(x) – многочлен степени kj-1, коэффициентами которого являются произвольные комплексные числа. Доказательство т.к. jC , j=1,..,s –корень хар-го многочлена l(t), то по Th 1 функции: e^1x, x*e^1x,..,x^(k1-1)*e^1x; e^2x, x*e^2x,..,x^(k2-1)*e^2x;…; e^sx, x*e^sx,..,x^(ks-1)*e^sx – решения (13). По Лемме эти ф-ции явл. линейно независ. на R. Число этих функций k1+k2+…+km=n. Следовательно, они образуют ФСР. yо.о.= j=1s (C1j+C2j*x+…+C(kj)j*x^(kj-1))*e^jx, где С – произвольные комплексные числа. Действительный случай Пусть a1, ..,anR (17) L[y]=y{n}+a1*y{n-1}+…+a(n-1)*y’+an*y=0 (15) l(t)=t^n+a1*t^(n-1)+…+a(n-1)*t+an=0
|
|
22. Решением системы (1) называется упорядоченный набор функций 1(x),.., n(x), определенных на I=<,> и удовлетворяющих условиям: 1) i=1,..,n : i(x)С^1(I) 2) xI : (x, 1(x),.., n(x)) 3) i=1,..,n xI : di(x)/dxfi(x, 1(x),.., n(x)) Определение Решением системы (1) называется вектор-функция (x)=( 1(x),.., n(x)) T, определенная на промежутке I и удовлетворяющая условиям: (x)С^1(I) 2) xI : (x, 1(x),.., n(x)) 3) xI : d(x)/dx= f(x. (x)) Определение Пусть (1(x),.., n(x)) T решение системы (1) на I. Интегральной кривой системы (1) называется кривая Rn+1x,y1,..,yn, заданная параметрически: ={x=x; y1=1(x);…; yn=n(x)}, xI Задача Коши Пусть f(x,y)=( f1(x,y),.., fn(x,y))T определена в и точка (x0,y01,..,y0n) Найти решение (x)=( 1(x),.., n(x)) системы (1) [(2)], удовлетворяющее условиям 1(x0)=y01, 2(x0)=y02,.., n(x0)=y0n. Запись в векторном виде: Обозначим y0=(y01,..,y0n)Rn Задача Коши dy/dx= f(x.y) – система, y(x0)=y0 – начальное условие. Геометрический смысл: - найти интегральную кривую, проходящую через эту точку Теорема (ТСЕ для НС n) Пусть f(x,y)=( f1(x,y),.., fn(x,y)) и f(x,y)/yi=(f1/yi,..,fn/yi), где i=1,..,n определена и непрерывна в области Rn+1x,y1,..,yn и (x0,y01,..,y0n)= (x0,y0) Тогда на некотором интервале I=(x0-,x0+) существует решение задачи Коши. dy/dx= f(x.y), y(x0)=y0 и это решение единственно. (без доказательства)
|
21. 2. Резонанс. l()=0, - корень кратности k многочленаl(t), т.е. l(t)=(t-)^k*l1(t), где l1(t)0. В этом случае L=l1(p)(p-)^k. Ищем yч.=Bx^k*e^x, где В подлежит определению. Уравнение (19) имеет вид L[y]=(l1(p)(p-)^k)[y]=Ae^x. Подставим yч. В уравнение: L[Bx^k*e^x]=B(l1(p)(p-)^k)[x^k*e^x]=B(l1(p))[(p-)^k*(x^k*e^x))]=B(l1(p))[k(k-1)…1*x^(k-k)e^x]=Bk!(l1(p)(e^x))=Bk!*l1()*e^x=Ae^x, где l1()0 <=> Bk!*l1()=A, B=A/(k!*l1() Замечание f(x)=e^x (Pm(x)cos(x)+Ql(x)sin(x)), Pm – многочлен степени m, Ql(x) – многочлен степени l. e^x=e^(+i)x=e^x*cos(x)+ e^x*isin(x), e^(-x)=e^(-i)x=e^x*cos(x)-e^x*isin(x) e^x*cos(x)=1/2(e^(+i)x+ e^(-i)x) e^x*sin(x)=1/2(e^(+i)x-e^(-i)x) f(x)=Pm(x)*e^x*cos(x)+Ql(x)*e^(-i)x =~Ps(x)*e^(+i)x+~Qs(x)e^(-i)x, где s=max(m,l), Ps(x), Qs(x) – многочлен с комплексными коэффициентами. Лемма Пусть L[y]=f1(x), L[y]=f2(x), L[y]=f1(x)+f2(x). Если 1(x) – решение L[y]=f1(x), 2(x) – решение L[y]=f2(x), то функция 1(x)+2(x) – решение уравнения L[y]=f1(x)+f2(x) На практике решение ищут в виде: 1. Нерезонансное, т..е. l(+i)0 yч.н.=e^(x)*(~Pl(x)*cos(x)+~Ql(x)*sin(x)) 2. Резонансное =(+i), l()=0 – корень кратности k. yч.н.=x^k*e^(x)*(~Pl(x)*cos(x)+~Ql(x)*sin(x))
|
|
|
|
|
|
|
25 Определение1. Вектор-функции 1(x)…n(x) назыв. лин. зав-ми на I=<>, если сущ-ют числа 1…n не все равные 0 такие, что xI: 11+…+nn0. Вектор-функции 1(x)…n(x) – лин. независимы на I, если из тождества xI: 11+…+nn0 следует, что 1=…=n=0. Определение2. Пусть на пром-ке I=<,> задана вектор-функция k(x)=(1k(x); 2k(x);…; nk(x))T (k=1…n) функциональный определитель W(x)=W[1(x)…n(x)]=|11(x)…1n(x);…;n1(x)…nn(x)| (это квадр. матрица размерами n×n) называется определитель Вронского системы функций 1(x)…n(x) на I=<>. Теор. Если система вектор-функций 1(x)…n(x) – линейно зависима на I, то xI: W(x)=W[1(x)…n(x)]0. Доказательство: Т.к. 1(x)…n(x) – лин. зав. на I, то сущ. числа 1…n не все равные 0, такие что xI: 11+…+nn0, след-но, x0I столбцы 1(x0)…n(x0) линейно зависимы W(x0)=W[1(x0)…n(x0)] т.к. его столбцы сов. с этими вект. В силу произвольности x0: W(x)=0 на I обратное неверно. Следствие. Если существует x0I в которой W(x0)=W[1(x)…n(x)]|x=x00, то вектор-функции 1(x)…n(x) – линейно независима на I.
|
26 Теор. Пусть вект.-функция 1(x)…n(x) явл-ся реш. dy/dx=A(x)y (1) на I. Если сущ. x0I, в которой W(x0)=W[1(x)…n(x)]|x=x0=0, то эти решения линейно зависимы на I. Доказательство: Рассм-м вектора 1(x0)…n(x0) –столбцы W(x). Они лин.зависимы, т.к. W(x0)=0. сущ. 1…n не все равные 0 такие, что 11+…+nn=0. Составим линейную комбинацию Z(x)=11(x)+…+nn(x). По теор(_1)Если 1(x)…m(x)- произвольные решения урав. dy/dx=A(x)y (или L[y]=0) и С1,..,Сm –произ. числа, то фун-ия y=С11(x)+..+ Сmm(x)-также решение урав (1). 2) Пусть U(x) и V(x)C1(I) действ. вект.-функции, если комплексная вект.-функция f(x)= U(x)+ i*V(x) - решение (1), то U(x) и V(x) решение (1). _) Z(x)–решение (1). Z0(x)=11(x0)+…+nn(x0)=0 Таким образом Z(x) реш. задачи Коши. dy/dx=A(x)y y(x0)=0 Такая задача (след.ТСЕ) имеет един. решение – нулевое решение, т.е.xI: Z(x)=0 .xI: 11(x)+…+nn(x)≡0, причем 1…n не все равные 0, след. 1(x)…n(x) – линейно зависимы. След.Если 1(x)…n(x) лин. незав. на I решения (1), то xI: W(x)=W[1(x)…n(x)]0 |
27 Пусть матрица-функция A(x)=||aij||n*n непрерывна на I=<>.dy/dx=A(x)y (1). Определение1. ФСР однородная сист. ЛДУ (1) порядка n назыв. любые n линейно независ. решений этой системы. Теор. У любой однор. системы ЛДУ существует ФСР. Доказательство: Зафиксируем x0I и вектора e1=(1,0,…,0)T, e2=(0,1,…,0)T,…,en=(0,0,…,1)T. Поставим задачу Коши: dy/dx=A(x)y, y(x0)=ek, k=1…n. Обозначим k(x) – реш. этой задачи. Покажем, что решение 1(x)…(x) линейно независимо. Вычислим: W(x0)=W[1(x0)…n(x0)]=|1,0,…,0;0,1,…,0;…;0,0,…,1|=10 (это квадр. матрица) 1(x)…n(x) – линейно независимы на I 1(x)…n(x) – ФСР. . Определение 2. Общим решением системы ЛДУ вида dy/dx=A(x)y+b(x) на промежутке I=<,> назыв. мн-во всех решений этой системы на I. Теор. (об общем решении системы ЛДУ). Пусть 1(x)…n(x) – ФСР системы (1) на пром. I, тогда любое решение этой системы имеет вид: y(x)=C11+…+Cnn, где C1…Cn – произвольные числа. |
|
28 dy/dx=A(x)y+b(x) (1); dy/dx=A(x)y (2); L=d/dx-A(x); L[y]= b(x) (1'); L[y]=0 (2'); b(x), A(x) непр. на I. Теор1. (св-ва решения неоднородной системы ЛДУ). 1. Если (x) – решение системы (1), а (x) – решение системы (2), то (x)+(x) – решение (1). 2. Если 1(x),2(x) – решения системы (1), то (x)=1(x)-2(x) – решение приведенной системы (2). Доказательство: 1. Дано L[]=b(x), L[]=0; L[+]=L[]+L[]=b(x)+0= b(x); +-решение (1). 2. Известно L[1(x)]=b(x), L[2(x)]=b(x). L[]=L[1-2]=Z[1(x)]-Z[2(x)]=b(x)-b(x)=0 (x)-реш.сист. (2). Теор2. (об общем решении неоднородных систем ЛДУ). Пусть (x) – частное решение системы (1), а 1(x)…n(x) – ФСР однородной системы (2), тогда любое решение y(x) неоднор. сист. (1) представ. в виде: y(x)=(x)+C11+…+Cnn, где C1…Cn – произвольные числа. Доказательство: Заметим, что любая вект.-функ. (x)-i=1nСii(x)- решение сист. (1) (из теор 1). Пусть y(x) – произвольное решение (1), тогда y(x)-(x)= (x), где (x)- реш. привед. сист. (2) (теор 1). По теор (_(об общем решении системы ЛДУ). Пусть 1(x)…n(x) – ФСР системы (1) на пром. I, тогда любое решение этой системы имеет вид: y(x)=C11+…+Cnn, где C1…Cn – произвольные числа._) (x) может быть представ. в виде: (x)=C11+…+Cnn, Следовательно, y(x)=(x)+(x)= (x)+C11+…+Cnn.
|
29. Метод вариации произвольных постоянных для неоднородной системы ЛДУ.
L=
Метод вариации произвольных постоянных:
Пусть
Теорема: если известна ФСР однородной системы (10) на промежутке I, то решение неоднородной системы (9) может быть найдено в квадратурах( выражено через интегралы известных функций) Док-во(метод нахождения частных решений системы (9)) :
где С1(x), … Cn(x) – непрерывно дифференцируемые функции на промежутке I, подлежащие определению. Определим: С1(x), … Cn(x)
По
условию : L[
|
30. ФСР однородной системы ЛДУ с постоянными коэффициентами с случае простых действительных корней характеристического уравнения. Система ЛДУ с постоянными коэффициентами
A=||aij||n×n
i,j=1,…n,
aij bk
(x)
Все решения системы (3) определены на всей числовой прямой, можно доказать, что все решения бесконечно дифференцируемы. Будем искать решения: y(x)= γ Теор 13. Пусть матрица A = ||aij||nn (aij C) имеет n различных собственных значений (хар чисел) 1…n,тогда век.-функ. y1=γ1*e1x … yn=γn*enx – где γk собств вектора, соотв. соб. знач. k (k=1,..n), образует ФСР сист. (3) и общее реш имеет вид y=C1 γ e1x +…+ Cn γnenx, где C1 … Cn – произв числа.
|
|
31. ФСР однородной системы ЛДУ с постоянными коэффициентами в случае, когда характеристическое уравнение имеет простые комплексные или кратные действительные корни. Система ЛДУ с постоянными коэффициентами
A=||aij||n×n
i,j=1,…n,
aij bk
(x)
Все решения системы (3) определены на всей числовой прямой, можно доказать, что все решения бесконечно дифференцируемы. Будем искать решения: y(x)= Теорема(1):
для того чтобы вектор-функция y=γeλx
являлась решением системы
Док-во: y=γeλx
– реш.сист. <=>
λγeλx=(Aγ)eλx<=>λγ=Aγ<=>Aγ=λγ следовательно согласно определению собственного вектора γ- собственный вектор матрицы А, соответствующий собственному значению λ матрицы А. 1)Пусть среди λ1, … λn встречаются комплексные числа. λ=α+β α,β - действительные числа λ- собственное значение, обозначается :γ≠θ – соответствующий собственный вектор. y=γeλx по теореме 1 – решение системы (5)
|
32.Понятие устойчивости по Ляпунову и ассимптотической устойчивости. Сведение исследования устойчивости решения к исследованию устойчивости нулевого решения. Реш.задачи
Коши: y= (1) Теория устойчивости Ляпунова Обозначим: y=y(t,y0) - реш.задачи Коши (1)-(2)
(1) Решение задачи (1),(2*) : y(t)=y(t,y0) Определение: Решение задачи (1),(2*) называется устойчивым по Ляпунову, если выполняется условие: 1) 2)
Определение: решение y=y(t,y0*) задачи (1),(2*) называется асимптотически устойчивым если: 1.оно устойчиво по Ляпунову 2.
|
33. Устойчивость системы ЛДУ. Необходимое и достаточное условие устойчивости линейной системы.
A(t)=|| В
этом случае задача Коши имеет
единственное решение, определенный
на [
Теорема
1. Решение
задачи Коши (3), Док-во:
обозначим:
=A(t)[
|

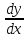 =A(x)y+b(x)
(9)
=A(x)y+b(x)
(9)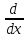 -
A(x), L[y]=b(x) (9’)
-
A(x), L[y]=b(x) (9’)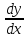 =A(x)y
(10), L[y]=
=A(x)y
(10), L[y]=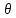 (10’)
(10’) 1(x),…
1(x),…
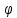 n(x)–
ФСР системы (10)
n(x)–
ФСР системы (10)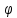 1(x),
…
1(x),
…
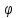 n(x)
– ФСР – ищем частные решения:
n(x)
– ФСР – ищем частные решения: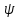 (x)=C1(x)φ(x)+…+
Cn(x)φn(x)=
(x)=C1(x)φ(x)+…+
Cn(x)φn(x)=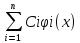 ,
,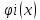 ]=o
i=1,
… n
]=o
i=1,
… n
 R(C)
R(C) C(I) k=1,…n,
I=<α,β>
C(I) k=1,…n,
I=<α,β>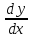 =Ay+b(x)
(2)
=Ay+b(x)
(2)
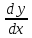 =
Ay
(3)
=
Ay
(3)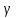 e^(
e^(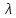 x)
(4), где λ
x)
(4), где λ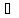 R(C)
R(C)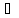 Rn
(Cn);
γ≠
Rn
(Cn);
γ≠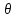

 R(C)
R(C) C(I) k=1,…n, I=<α,β>
C(I) k=1,…n, I=<α,β>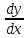 =Ay+b(x)
(2)
=Ay+b(x)
(2)
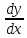 =
Ay (3)
=
Ay (3)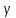 e^(
e^(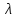 x)
(4), где λ
x)
(4), где λ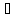 R(C)
, γ
R(C)
, γ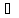 Rn
(Cn);
γ≠
Rn
(Cn);
γ≠
 =Ay
необходимо и достаточно, чтобы λ было
собственным значением матрицы А, а γ
собственным вектором, соответствующим
собственному значению.
=Ay
необходимо и достаточно, чтобы λ было
собственным значением матрицы А, а γ
собственным вектором, соответствующим
собственному значению. γeλx
γeλx
 A(γeλx)
A(γeλx) γeλx=γ(deλx)/dx
= γeλx
=
λγeλx
γeλx=γ(deλx)/dx
= γeλx
=
λγeλx
 (t)
(t)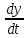 =F(t,y)
(2)
y(t0)=y0
=F(t,y)
(2)
y(t0)=y0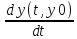 =F(t,y(t,y0));
y(t0,y0)=y0
=F(t,y(t,y0));
y(t0,y0)=y0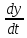 =F(t,y)
(2*)y(t0)=y0
=F(t,y)
(2*)y(t0)=y0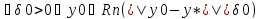 задача Коши имеет единственное решение
y=y(t,y0)
опред на [t0:+
задача Коши имеет единственное решение
y=y(t,y0)
опред на [t0:+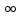 ]
]
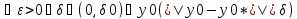
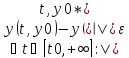

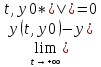
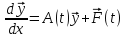 (3)
(3)
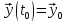
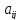 (t)|
(t)|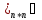 C[
C[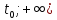
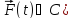

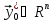
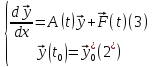
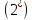 устойчиво (ассимтотически устойчиво),
если нулевое решение приведенной
однородной системы ЛДУ:
устойчиво (ассимтотически устойчиво),
если нулевое решение приведенной
однородной системы ЛДУ: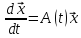
 где
где
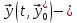 решение (3),
решение (3),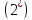
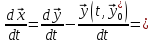 [А(t)
[А(t)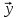 +
+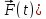 -[A(t)
-[A(t)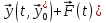 =
=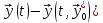 =
=