
Шпоры.Диффуры.3 сем
.docx
Пусть - область в пространстве Rn+2 и в задана функция F(x,y,U1,…,Un). Опр 1. Обыкновенным дифференциальным уравнением порядка n называется выражение вида: F(x,y,y1,…,y(n))=0 (1), где x - независимая переменная, y(x)-функция от x, y1(x),...,y(n)(x) -производная от y(x), n-порядок. Опр 2. Функция y=(x) определенная на промежутке I=<,> называется решением дифференциального уравнения (1), если выполняются условия : 1) (x)Cn(I); 2)xI: точка с координатами (x, (x), 1(x)…(n)(x)); 3) xI: F(x,(x),1(x),…,(n)(x))=0 Пусть D-область, D<Rn+1 X ,Y ,U1 , …, Un-1 В D определена функция f(x,y,u1,…,un-1) Если F(x,y,u1,…,un)= un -F(x,y,u1,…,un-1), где F(x,y,u1,…,un-1) определена в D Rn+1, то уравнение f(x,y,y1,…,y(n-1))= y(n) называется разрешенным относительно старшей производной.
|
2. ОДУ первого порядка, разрешенные относительно производной. Понятия решения и интегральной кривой уравнения. Постановка задачи Коши. Пусть область DR2 и f(x,y) определена в D. y’=f(x,y) (1) - ОДУ 1-го порядка разрешенная относительно производной. Опр 1. Функция y=(x) определена на промежутке I=<,> называется решением уравнения (1) если: 1) (x)C1(I); 2) xI:(x,(x))D 3)xI: '(x)=f(x,(x)). Опр 2. Если y=(x)- решение (1), то график этой функции называется интегральной кривой уравнения (1). Постановка задачи Коши. Известно: Область DR2, f(x,y)-определена в D и точка (x0,y0)D (или числа (x0,y0)D).Надо найти решения y=(x) уравнения (1) определенное на I, такое что (x0)=y0 (т.е. интегральная кривая проходящая через (x0,y0)). Числа (x0,y0) называются начальными условиями. Условная запись задачи Коши. Найти решение y’=f(x,y) удовлетворяющее условию y(x0)=y0. Замечания
|
3. Формулировка теоремы существования и единственности ( ТСЕ ). Понятие общего решения. Обобщение некот понятий. Пусть f(x,y) опред обл DR2 X ,Y , точка (x0,y0)D. Рассмотрим задачу Коши (8)(y’=f(x,y)(2);y(x0)=y0). Пусть 1(x) и 2(x) решения (8), т.е. 1(x),2(x)-реш(2) и 1(x0)=y0, 2(x0)=y0. Опред. Говорят, что задача Коши(8) имеет единст решение если любые 2 реш 1(x) и 2(x) этой задачи совпадают на некот окр-сти точки x0 >0 x(x0-,x0+):1(x)2(x) ТСУ1(Локальная)Пусть на обл. DR2 X ,Y функ.f(x,y) и ее част. производная (x/y)(x,y) опред. и непрерывны, и точка (x0,y0) D. Тогда урав. y’=f(x,y) имеет решение (x): 1)опред. на некот. окр-сти (x0-h,x0+h) точки x0, удовл. условию (x0)=y0; 2)такое решение единственно.(Без док-ва) Замечание к ТСЕ. Пусть в обл D выполн. усл. ТСЕ1. 1)В D беск много решений уравнений. x0-точка(x0,y0)D.Через эту точку проходит реш y=(x,y0).Все эти решения не совпадают. 2)Решение задачи(8) может быть опред-но лишь на некот окр-сти x0. Пусть f(x,y) удовл в D условиям ТСЕ1. Функцию y=(x,c) наз-ют общим решения урав(2) в обл D, если: 1)c:(x,c)-реш(2); 2) частное решение урав(2) может быть получено из (x,c) подбором соотве-его значения c.
|
|
4. Уравнения с разделяющимися переменными. Однородные уравнения. Уравнения с разделяющимися переменными: y’=f(x)*g(y) (3) Теорема 1. Пусть функция f(x)-непрерывна на интервале (a,b), а функция g(y)-непрерывна на (c,d) причем для y(c,d): g(y)0. Тогда через любую точку прямоугольника D={(x,y),a<x<b,c<y<d} проходит единственное решение уравнения (3). Док-во. y’=f(x)*g(y) (3); g(y) ≠0; (3’): y’/g(y)=f(x). Проинтегрируем (3’) по х y’dx/g(y)=f(x)dx dy/g(y)= f(x)dx (3*) Это равенство множества первообразных. Обозначим F(x)= x0xf(t)dt, G(y)= y0yds/g(s). Из (3*) G(y)=F(x)+C. Т.к. G’(y)=1/g(y)≠0, то у G(y) существует обратная G-1. y= G-1(F(x)+C)-решение урав(3). Найдем реш., прох. (x0,y0). G(y0)=F(x0)+C -> 0=0+C=0. y=G-1(F(x)) проходит через (x0,y0).
|
5.Линейные уравнения первого порядка. Уравнения Бернули. Ур-е вида(1) y/+p(x)=f(x) – линейное ур-е 1ого порядка. Теор. Пусть функция р(х) и f(x) непрерывны на интервале α<x<β. Тогда через любую точку(х0;у0) полосы D={(х;у); α<x<β, -∞<y<+∞}проходит единственное решение ур-я (1) причем оно определено на (α;β). Уравнение(1) однородное, если f(x)≡0 и неоднородно в противном случае. Док-во(Метод решения): 1) Пусть ур-е однородное, т.е y/+p(x)=0 – это ур-е с разделяющимеся переменными. у≡0 – решение; у≠0, dy/y=-p(x)dx, ∫dy/y=-∫p(x)dx,ln|y|=-∫x0X p(t)dt + lnC1, C1>0, lnC1 ϵ |R Потенциируем выражение |y|=C1exp(-∫x0X p(t)dt), y=± C1exp(-∫x0X p(t)dt), C1>0 {C1,y>0 => Введем новую С={-C1,y<0 => y=Cexp(-∫x0X p(t)dt), разрешим С=0,С ϵ |R Решение проходит через(х0;у0) имеет вид y = y0exp(-∫x0X p(t)dt) 2) Пусть f(x)≠0/ Решаем ур-е (1)
|
6.Обобщенное понятие интегральной кривой. D
1)
φ(t),
ψ(t)
3) Опред2| Если интегральная кривая ур-я (1) задаётся в виде Ф(х,у)=0, то это ур-е будем называть интегралом ур-я (1). Опред3|
Уравнение Ф(х,у)=С называется общим
интегралом ур-я (1), если1)
Ур-е
в полных дифференциалах: Пусть P(x,y)
и Q(x,y)
(2)
dU(x,y)=
P(x,y)dx+
Q(x,y)dy=0,
ясно что dU(x,y)=
0
|
|
7.Уравнения первого порядка, не разрешенные относительно производной. Пусть
в обл. в G Рассмотрим
функцию F(x,y,U1)
опред. на G Постановка
задачи Коши: Пусть F(x,y,p)
опред.в обл. в G Опред| Решение ур-я F(x,y,у(1))=0, через каждую точку которого, проходит ещё одно решение, касаясь того же направления, называется особым решением этого ур-я. |
8.Общий метод введения параметра. F(x,y,у(1))=0 ур-е 1ого порядка неразреш. отн. производной. Будем искать решение (интегральную кривую) в параметрическом виде(2) γ {х=х(р), у=у(р), рϵ < α, β>. Вводим параметр у(1)=р. Сводим уравнение к разрешенному отн. производной у=f(x, у(1)) или x=g(y, у(1)). Решение ищем в виде γ {х=х(р), у=у(р), γ
{х=х(р), у=f(x(р),p),
p=p(x),
p(1)(x)≠0.
Рассм. равенство: у=f(x,p)
и продиффер. его по х,считая р=р(х);
(1*)
рх(1)р= |
|
|
|
|
|
|
Теор1|
Пусть D-односвязная
область в |R2x,y
функции P(x,y),Q(x,y)
непрер. И диффер. на D.
Тогда ур-е P(x,y)dx+
Q(x,y)dy=0
явл. ур-ем в полных диффер., если
Док-во:1)
Необходимость. Пусть ур-е явл. ур-ем в
полных диффер.,т.е
dU=
P(x,y)dx+ Q(x,y)dy. Известно
что dU=U(1)x
dx+
U(1)y
dy
значит
Нахождение
первообразной: dU(x,y)=
P(x,y)dx+
Q(x,y)dy=0-
ур-е в полных диффер.; dU=U(1)xdx+
U(1)ydy,т.е
U(1)x=Р(х,у),
U(1)y=Q(x,y),
U(x,y)=∫P(x,y)dx+
g(y),
g(y)-непр.диффер.подлежит
определению.
|
Выпишем все решение ур-я y/+p(x)=0, y=Cexp(-∫x0X p(t)dt), оно представляется в виде у= φ(x). Св-ва
φ(x):1)
φ(x)
ϵ С1(α;β)
3)
φ(x)
– решение уравнения
y/+p(x)=0
на
(α;β), т.е
Подставим у=φ(x)С(х) в (1) y(1)=C(1)(x)φ(x)+C(x) φ (1)(x), [C(1)(x)φ(x)+C(x) φ (1)(x)]+p(x)C(x) φ(x)=f(x), т.к C(1)(x)φ(x)+ p(x)C(x) φ(x) ≡0, то C(1)(x)φ(x)=f(x), т.к φ(x)>0 на(α;β) C(1)=f(x)/ φ(x) – непрерывно на (α;β) С(x)= ∫x0Xf(s)/ φ(s)dS + K,K ϵ|R Подставим С(x) в y(x): y(x)= φ(x) ∫x0Xf(s)/ φ(s)dS + K φ(x) Замечание| yо.н=уо.о+уч.н Решение проходит через(х0;у0), y(x)= φ(x) ∫x0Xf(s)/ φ(s)dS + у0 φ(x)=>y(x0)= φ(x0) ∫x0X0f(s)/ φ(s)dS + у0 φ(x0)=0+y0*1=y0 Ур-е вида(2) y/+p(x)=y(n)f(x)- ур-е Бернули. n≠0,n≠1. Если n>0,то y≡0 – решение, =>y≠0 то делим обе части ур-я на y(n), Вводим новую переменную z(x)=y(1-n), z(1)(x)= (y(1-n))(1)=(1-n)y(-n)y(1), z(1)+(1-n)p(x)z=(1-n)f(x) – линейное относ. z
|
Замечание. 1) Если существует y* такое что g(y*)=0, то функция y= y*-общее решение уравнения (3). 2) Схема решения (3): а) g(y)=0 находим y*. Функция y= y*-общее решение уравнения (3) б) g(y)0. Разделяем переменные dy/g(y)=f(x)dx. Интегрируем dy/g(y)=f(x)dx+C. y’=f(ax+by+c) a,bR, b0 x-независимая переменная. Вводим z(x)=ax+by. zx’=a+byx’ yx’=1/b*(zx-a). Разделяем переменные 1/b*(zx’-a)=f(z) zx’=bf(z)+a-уравнение с разделяющимися переменными. Однородные уравнения. dy/dx=f(x/y) (1) - однородное, x-независимая переменная. u=u(x)=y/x, y=xu, yx’=u+xux’. Подставим в (1) u+xux’=f(u), xux’=f(u)-u, ux’=(f(u)-u)/x. Уравнения сводящиеся к однородному. yx’=f[(a1+b1y+c1)/( a2+b2y+c2)]. a1b2-b1a20 { a1+b1y+c1=0; a2+b2y+c2=0. Пусть решение системы в точке (x0,y0). Разделим переменные {y*=x-x0;y*=y-y0} dy*/dx*=dy/dx, dy*/dx*=f((a1x*+b1y*)/( a2x*+b2y*))-однородная относительно x*, y*.
|
|
|
|
|
|
9. Уравнения Лагранжа и Клеро. Ур-ие Лагранжа: y=f(y’)*x+g(y’) (1); f(y’) ≠y’; y’=p; {x=x(p),y=y(p); {x=x(p),y=f(p)*x+g(p); yx’=f(p)+x*df/dp* px’+dg/dp* px’; p-f(p)=x*df/dp* px’+dg/dp* px’; Если p-f(p) ≠0 и т.к. px’≠0; (p-f(p))* xp’=x*df/dp+dg/dp лин. ур-ие относит. x(p). Если сущ-ет p0 такое, что f(p0)= p0=0, т.е. f(p0)= p0 то ур-ие (1) имеет реш-ие вида; y=f(p0)+g(p0) или y= p0*x+g(p0)); Ур-ие Клеро: y=x*y’+g(y’)(2); вводим параметр p=y’; {x=x(p), y=x*p+g(p); yx’=p+x* px’+ gp’*px’; p = p + x*px’ + gp’*px’; [x + gp’(p)]*px’ = 0; a) px’=0 p=c; y=c*x+g(c) семейство прямых( реш ур-ия (2)); б) x+g’(p)=0x=-g’(p); Уравнение интегральной кривой γ : {x = - g’(p); y = - p*g’(p) + g(p); Пусть g(p) ЄC1(I), g’’≠0; в этом случае γ-особая интег-ая кривая(2), пусть p0Є I : (x0;y0) Є γ; { x0 =-g’(p0), y0=- p0g’(p0)+g(p0) Для γ в точке (x0;y0) yx’ - тангенс угла наклона касательной yx’ (x0;y0)= p0; y=c*x+g(c); {x0=-g’(p0), y0=- p0*g’(p0)+g(p0)=c* x0+g(c); yx’(x0)= p0=c; c= p0; реш-ие y= p0*x+g(p0) проходит через точку (x0;y0) касаясь интегр-ой кривой особая инт-ая кривая γ γ-особая интегр-ая кривая.
|
10. ОДУ порядка n: определение решения, постановка задачи Коши, формулировка ТСЕ. Пусть Ω область в пр-ве Rn+1 и в Ω задана непрер. ф-я f(x, y, U1 , …, Un-1) Соотношение y(n) = f( x, y, y’, ... , y(n – 1) )(1) вида называется ОДУ порядка n, разрешенным относительно старшей производной. Опр.: Ф-я φ(x) определенная на промежутке I=<α;β>, наз-ся реш-ем ур-ия (1), если вып-ся след. условия:1) φ(x) Є Сn(I); 2) x Є I точка : (x ,φ(x), φ’(x) ,…, φ(n-1)(x)) Є Ω; 3) x Є I точка : φ(n)(x) ≡ f(x, φ(x), φ’(x), …, φ(n-1)(x)). Постановка задачи Коши. Пусть Ω обл пр-ва Rn-1 , f(x, y, U1 , …, Un-1) определена и непрер в Ω , числа (x0, y0 , y0’,…, y0 (n-1) ) такие, что (x0, y0 , y0’,…, y0 (n-1) ) Є Ω. Найти ф-ю , опред на интервале (x0-δ; x0+δ) являющ реш-ем ур-ия (1) и удовлет усл y0 = φ(x0), y0’= φ’(x0),…, y0 (n-1) = = φ(n-1)(x0) нач данные: (x0, y0 , y0’,…, y0 (n-1) ). Запись задачи Коши: y(n) = f(x,y,y’,... ,y (n – 1) ) , y(x0) = y0 , y’(x0) = y0’ , … , y(n-1)(x0) = y0 (n-1) . TCE 2( локаль): Пусть Ω область в Rn+1 , (x0, y0 , y0’,…, y0 (n-1) ) ,численно, такие, что (x0, y0 , y0’,…, y0 (n-1) ) Є Ω. Если ф-я f(x, y, U1 , …, Un-1 )и частн призв ∂f /∂ui (x, y, U1 , …, Un-1 )(i=1,…,n-1) непрер в обл Ω, то в некоторой окрест =(x0-h; x0+h) сущ реш-я ур-ия y(n) = f( x, y, y’, ... , y(n – 1) ), и это реш-ие удовлет усл y(x0) = y0 , y’(x0) = y0’ , … , y(n-1)(x0) = y0 (n-1) и это реш-ие единственно. Физический смысл: x(t) – координата точки массы m на оси x. x’= dx/dt - это скорость; x’’=d2x/dt2 - это ускорение ; f(t, x, x’) – это сила , действующая на точку. m*x’’ = f(t, x, x’). Начальные условия : {t0 – нач момент времени; x(t0) – нач координата; x0’ – нач скорость {m*x’’ = f(t, x, x’); x(t0) = x0; x’(t0) = x0’. |
11.Простейшие методы понижения порядка. Примеры. (1) F(x, y, y’, ... , y (n)) = 0 – называется неразрешённым относительно старшей производной. I.F(x, y’, y’’, ... , y (n) ) = 0 – функция не содержит y. Осуществим замену переменной: х – независимая переменная; z(x) = y’(x) , y’’= z’,…,y(n) = z(n-1) F(x, z, z’, … , z(n-1) ) = 0. II. Левая часть не содержит (явно) x. F( y, y’, y’’... , y (n) ) = 0; у – независимая переменная; t = t(y) = yx’; t – функция от у. yxx’’ =(ух’)х’ = tx’= ty’*yx’= t*ty’ yxxx’’’ = (yxx’’)’ = (t*ty’)x’ = (t*ty’)y’*yx’ = t*(t*ty’)y’ F(y, t, ty’... , t (n-1) ) = 0. III. F(x, y, y’, ... , y (n)) = 0; Пусть Ф(x, y, y’, ... , y (n-1)) такая, что F(x, y, y’, ... , y (n)) = d/dxФ(x, y, y’, y’’, ... , y (n-1) ), тогда исходное ур. эквивалентно Ф(x, y, y’, y’’, ... , y (n-1)) = C. Пример. y*y’’ + y’2 = 1. Решение: (Х)х’ = 1; (y*y’)’ = y*y’’ + y’*y’; (y*y’)x’ = (Х)х’; y*y’ = x + C1; ∫y*dy = ∫(x + C1)dx; y2/2 = x2/2 + C1*x + C2; y2 = x2 + 2*C1*x + 2*C2; K1 = 2*C1; K2 = 2*C2 . Ответ: y2 = x2 + K1*x + K2 .
|
|
12.Линейное дифференциальное уравнение (ЛДУ) порядка n. Формулировка ТСЕ и задачи Коши для ЛДУ высшего порядка. Пусть a0(x), a1(x), … , an(x), f(x) определены на I=<α,β>. Уравнение вида a0(x)*y(n) + a1(x)*y(n-1) + … +an-1(x)*y’ + an(x)*y = f(x) называется ЛДУ порядка n (a0(x) ≠ 0). Если a0(x) ≠ I на I, то обозначим: Pi(x) = ai(x)/a0(x); I = 1,…,n; f(x) = b(x)/a0(x); (1) y(n) + p1(x)*y(n-1) + … + pn-1(x)*y’ + pn(x)*y = f(x); Если для всех xЄ I выполняется f(x) ≡ 0, то (2) y(n) + p1(x)*y(n-1) +…+pn-1(x)*y’ + pn(x)*y = 0. Ур. (1) – неоднородное ЛДУ порядка n; Ур. (2) – однородное ЛДУ порядка n. Постановка задачи Коши. Пусть x0 Є I, y0 , y0’,…, y0 (n-1) - произвольные действ.числа. Найти решение ур. (1), удовлетворяющее начальным условиям: y(x0) = y0 , y’(x0) = y0’ , … , y(n-1)(x0) = = y0 (n-1). Теорема. (ТСЕ 3 - для ЛДУ порядка n). Пусть функции p1(x) , … , pn(x) , f(x) непрерывны на промежутке I=<α,β> , точка х0 Є I, y0 ,y0’ , … , y0 (n-1) - произвольные действ. числа . Тогда существует единственное решение уравнения (1), удовлетворяющее начальному условию: y(x0) = y0 , y’(x0) = y0’ , … , y(n-1)(x0) = y0 (n-1), определённое на всём промежутке I=<α,β>. Замечание к ТСЕ 3. Пусть x0 Є I, ур. (2) – однородное, и начальные условия: y(x0) = 0 , y’(x0) = 0 , … , y(n-1)(x0) = 0. Эта задача Коши имеет только нулевое решение y ≡ 0.
|
16. Теор. Пусть p1(x),…, pn(x) ∈C(I),тогда пространство решений однородного ЛДУ (7) L[y]=0= y(n)+ p1(x) y(n-1) +….+ pn(x) y порядка n конечномерно , и его размерность равна n. Док-во. Укажем базис в пространстве решений уравнения (7) Зафиксируем точку x0 ∈I y1 (x0)=1 , y(1) (x0)=0,…., y(n-1) (x0)=0 По ТСЕ эта задача имеет единственное решение , определенное н а всем промежутке I. Рассмотрим задачу Коши для уравнения (7) с начальными условиями. y(k)(x0)=1, y(i)(x0)=0 I не равно K Эта задача имеет решение .Обозначим его yk+1 (x) Получим систему решений уравнения (7)
Эти решения линейно независимы.
|
|
|
13.ЛДУ порядка п и линейный дифференциальный оператор. Свойства решений однородного ЛДУ. Пусть p1(x)…pn(x) непр на I=<a;b> Рассм. оператор L, L: c^(n)->c(I)
L=d^n/dx^n
+P1(x)d^(n-1)/dx^(n-1)+...+Pn-1(x)D/dx+Pn(x)D^0/dx^0;
d^0/dx^0(f)=f ^0 = f
Теор.
Пусть Р1(х)…Рn(х) 1)
Если У1(х) и У2(х) – реш-я ЛДУ пор-ка n,
и
2)Если комплекс. Функц. F(x)=U(x)+iV(x) Реш. ур-я ЛДУ пор n, то действ часть ReF(x)=U(x) и JmF(x) = iV(x) – реш-е ур-я ЛДУ пор n. |
14 Линейно зависимые и линейно независимые системы функций. Определитель Вронского и необходимое условие линейной зависимости произвольной системы функций. Определитель Вронского системы ф-ций. Услов. линейной зав ф-ции.
1)Пусть
ф-ции
х
2)Функ.
Пусть
y1(x),y2(x)…
Опр-ль
вида
W(x)=W(y1(x),y2(x)… Наз-ся опред-лем Вронского |
15 Теорема об определителе Вронского системы линейно независимых решений однородного ЛДУ порядка п. Т1
Пусть решения y1(x),y2(x)… Если
y1(x),y2(x)…
Следствие:
Если сущ-т X0,
такое, что W(Х0)=0,
то y1(x),y2(x)… |
|
|
|
|
|
|
Пусть φ (x)-произвольное решение уравнения (7) Вычислим значение φ (x), φ' (x) ….. в x0∈I Обозначим a1= φ (x0), ,…, an= φ (n-1) (x0) Построим z(x)= a1 y1 (x)+….+ an yn (x)- φ (x) Z(x)-решение уравнения (7) z(x0)= a1 y1 (x0)+….+ an yn (x0)- φ (x0)=0 и все производные тоже равны 0. Итак ,решение уравнения (7) z(x) удовлетворяет начальным условиям z(x0)=0,и все остальные производные равны нулю. Следовательно по замечанию к ТСЕ3, решение z(x)=0 z(x)= a1 y1 (x)+….+ an yn (x)- φ (x)=0 y1 (x), ……..,yn(x)-базис в пространстве решений уравнения Замечание ТСЕ 3. Если z(x)= a1 y1 (x)+….+ an yn (x)- φ (x)=0 и y(x0)=0 как и все производные y, то эта задача Коши имеет только нулевое решение y=0. |
|
|
|
|
|

 |R2
Опред.1|
Пусть P(x,y)
и Q(x,y)
непрерывны в обл.D.
Кривая γ ={(x,y),
x=φ(t),
y=ψ(t),
t
|R2
Опред.1|
Пусть P(x,y)
и Q(x,y)
непрерывны в обл.D.
Кривая γ ={(x,y),
x=φ(t),
y=ψ(t),
t I=<
α, β>} называется интегральной кривой
ур-я (1)P(x,y)dx+
Q(x,y)dy=0,если
выполняются условия:
I=<
α, β>} называется интегральной кривой
ур-я (1)P(x,y)dx+
Q(x,y)dy=0,если
выполняются условия: С1(I)
2)
С1(I)
2)
 I:
(φ(t),
ψ(t))
I:
(φ(t),
ψ(t)) D
D I:
P((φ(t),
ψ(t))
φ
(1)(x)+Q((φ(t),
ψ(t))
ψ(1)(t)≡0
I:
P((φ(t),
ψ(t))
φ
(1)(x)+Q((φ(t),
ψ(t))
ψ(1)(t)≡0 :
Ф(х,у)=С – интеграл ур-я (1) ;2) Любой
интеграл ур-я можно получить подбором
соответствующих произвольныз постоянных
С.
:
Ф(х,у)=С – интеграл ур-я (1) ;2) Любой
интеграл ур-я можно получить подбором
соответствующих произвольныз постоянных
С. С1(D),
ур-е P(x,y)dx+
Q(x,y)dy=0
называется ур-ем в полных дифференциалах
,если
С1(D),
ур-е P(x,y)dx+
Q(x,y)dy=0
называется ур-ем в полных дифференциалах
,если
 U(x,y)
U(x,y) С1(D),
такая что dU(x,y)=
P(x,y)dx+
Q(x,y)dy
С1(D),
такая что dU(x,y)=
P(x,y)dx+
Q(x,y)dy U(x,y)=С.
Докажем что U(x,y)=С
– общий интеграл ур-я(2): пусть γ ={(x,y),
x=х(t),
y=у(t),
t
U(x,y)=С.
Докажем что U(x,y)=С
– общий интеграл ур-я(2): пусть γ ={(x,y),
x=х(t),
y=у(t),
t I=<
α, β>}- интегральная кривая(2)
P(x(t),y(t))x(1)tdx+
Q(x(t),y(t))y(1)tdy=0=
dU(x(t),y(t))
– т.е существует С
I=<
α, β>}- интегральная кривая(2)
P(x(t),y(t))x(1)tdx+
Q(x(t),y(t))y(1)tdy=0=
dU(x(t),y(t))
– т.е существует С |R
такое что
|R
такое что
 γ: U(x,y)=C
γ: U(x,y)=C |R3х,у,р
опред.
непр. Функция F(x,y,p)
и ур-е F(x,y,p)=0
имеет хотя бы 1 решение в обл. G.
Говорят,что урав. F(x,y,p)=0
задает в обл. D
|R3х,у,р
опред.
непр. Функция F(x,y,p)
и ур-е F(x,y,p)=0
имеет хотя бы 1 решение в обл. G.
Говорят,что урав. F(x,y,p)=0
задает в обл. D |R2x,y
функцию p=f(x,y),если:1)
|R2x,y
функцию p=f(x,y),если:1)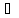 (x,y)ϵD:
((x,y),f(x,y))ϵG.
2)
(x,y)ϵD:
((x,y),f(x,y))ϵG.
2) (x,y)ϵD:
F(x,y,f(x,y))≡G.
В этом случае p=f(x,y)
неявно задается ур-ем F(x,y,p)=0.
(x,y)ϵD:
F(x,y,f(x,y))≡G.
В этом случае p=f(x,y)
неявно задается ур-ем F(x,y,p)=0.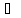 |R3.
(1) F(x,y,у(1))=0
ур-е 1ого порядка неразреш. отн.
производной.
|R3.
(1) F(x,y,у(1))=0
ур-е 1ого порядка неразреш. отн.
производной.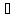 |R3х,у,р
, точка(х0,у0,р0)ϵ
G
и F(x,y,p)=0.
Найти φ(x)решение
ур-я F(x,y,p)=0
оперд. на некотор. окрестности
(х-h,x+h)точки
х0
и уд. усл. φ(x0)=у0,
φ(1)(х0)
=р(х0).
Запись задачи Коши: F(x,y,у(1))=0,
у(х0)
=у0
у(1)(х0)
=у(1)0,
где F(x0,y0,у(1)0)=0
|R3х,у,р
, точка(х0,у0,р0)ϵ
G
и F(x,y,p)=0.
Найти φ(x)решение
ур-я F(x,y,p)=0
оперд. на некотор. окрестности
(х-h,x+h)точки
х0
и уд. усл. φ(x0)=у0,
φ(1)(х0)
=р(х0).
Запись задачи Коши: F(x,y,у(1))=0,
у(х0)
=у0
у(1)(х0)
=у(1)0,
где F(x0,y0,у(1)0)=0
 =
=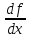 +
+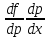 т.к
т.к
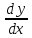 =
у(1)=р.
(1)р=f(1)x+f(1)pp(1)x
ур-е (1) разреш. отн. произв р(1)х.
Т.к р(1)х≠0
и х(1)р=1/р(1)х;
=
у(1)=р.
(1)р=f(1)x+f(1)pp(1)x
ур-е (1) разреш. отн. произв р(1)х.
Т.к р(1)х≠0
и х(1)р=1/р(1)х;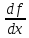 х(1)р+
х(1)р+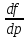 .
Решаем (1*), находим х(р), подставляем в
(2).
.
Решаем (1*), находим х(р), подставляем в
(2).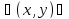 D:
D:
 =
=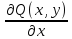 .
. U(x,y)
U(x,y) C1(D)
C1(D)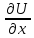 =P(x,y);
=P(x,y);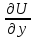 =Q(x,y).
P,Q
=Q(x,y).
P,Q C1(D)
след-но сущ. непрер.
C1(D)
след-но сущ. непрер.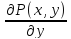 =
=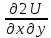 ,
,
 =
=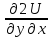 ,
т.к
,
т.к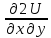 и
и
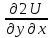 - непр. То .
- непр. То .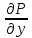 =
=
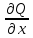 .
.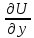 =
=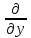 (∫P(x,y)dx+
g(1)(y))=
Q(x,y).
Сначала находим g(1)(y)
и g(y)
и подставляем g(y)
в U(x,y).
(∫P(x,y)dx+
g(1)(y))=
Q(x,y).
Сначала находим g(1)(y)
и g(y)
и подставляем g(y)
в U(x,y).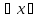 (α;β):
φ(x)>0.
2) φ(x0)≡
exp(-∫x0X0
p(t)dt)=1
(α;β):
φ(x)>0.
2) φ(x0)≡
exp(-∫x0X0
p(t)dt)=1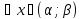 φ
(1)(x)+p(x)
φ(x)≡0.
Решение уравнения (1) ищем в виде y=C(x)
φ(x),где
С(x)непрерывно
дифференцируема на (α;β),подлежит
определению.
φ
(1)(x)+p(x)
φ(x)≡0.
Решение уравнения (1) ищем в виде y=C(x)
φ(x),где
С(x)непрерывно
дифференцируема на (α;β),подлежит
определению. ;
;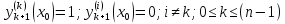
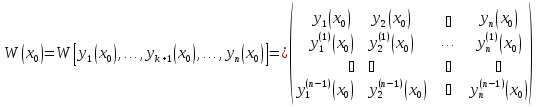
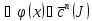 ;
;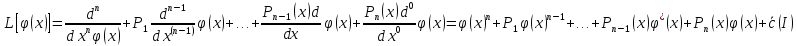
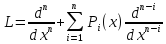
 С(I)
С(I)
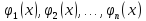 наз-ся лин зав-ми на I,
если найдутся числа
наз-ся лин зав-ми на I,
если найдутся числа
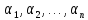 не все равные нулю, такие, что на I
выполняется тождество:
не все равные нулю, такие, что на I
выполняется тождество: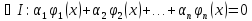
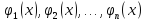 наз-ся лин. незав. на I,
если выполн тожд-во:
наз-ся лин. незав. на I,
если выполн тожд-во: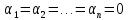
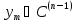 (I)
(I)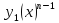
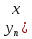 )=
)=
 – лин незав на I.
– лин незав на I. - лин незав на I,
то
- лин незав на I,
то
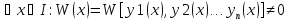
 - лин зав на I
- лин зав на I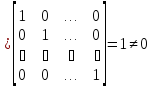
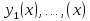 — линейно
независимы (по следствию 4)
— линейно
независимы (по следствию 4)