16. Метод Ньютона решения систем.

Рассм-м систему: / f₁(x₁…x_n)=0

\ f_n(x₁…x_n)=0 OR f(x)=0

Предположим, что найденоx^(p)=(x₁^(p) …x_n^(p)) приближение, одного из его кoрней, тогда точный корень может быть предложен в виде:

x=x^(p)+ ^(p) , где ^(p)=(₁ ^(p)… _n^(p)) явл-ся погрешностью, т.е. ур-е может быть записано в видеf(x^(р) + ^(p))=0 Разложим левую часть ур-я по степеням  ограничившись линейными членами:

f(x^(р)+ ^(p))= f(x^(р) )+ f’(x^(р) )* ^(p) Перепишем это ур-е в развернутом виде:

f₁(x₁^(р)+₁ ^(p)…x_n^(р)+_n ^(p))= f₁(x₁^(р) ..x_n^(р)) +f’_1x1(x₁^(р)…x_n^(р))*₁ ^(p)+..+f’_1xn(x₁^(р)…x_n^(р))*_n^(p)

F_n(x₁^(р)+₁ ^(p)…x_n^(р)+_n ^(p))= f_n(x₁^(р) …x_n^(р))+f’_{n x1}(x₁^(р)…x_n^(р))*₁ ^(p)+…+f’_{n xn}(x₁^(р)…x_n^(р))*_n^(p) Т.е. матрица f’(x) явл-ся матрицей Якоби. Иначе f’(x)= W(x)=[f _i /x _j] _{ij =1,n} Исходная система имеет вид: f(x^(р))+W(x^(р))*^(p)=0=> W^-1(x^(р))*f(x^(р))+^(p)=0 ^(p)= -W ^-1(x^(р))*f(x^(р)) Подставляя в исходное:

x^(р+1)=x^(р)- W ^-1(x^(p))*f(x^(p))

17. Теорема о сходимости метода Ньютона. Модиф-й метод Ньютона.

(дост-е усл-я сх-ти) Теорема: Пусть дана нелинейная системаf(x)=0 или

f(x)=/ f₁(x₁…x_n)

\ f_n(x₁…x_n)

где ф-ии f₁…f_n определены и непрерывны вместе со своими частными производными 1го и 2го порядка. Пусть x⁽⁰⁾ – некоторое начальное условие. И пусть выполнено:

1)Якобиан имеет обратную матрицу W^-1(x⁽⁰⁾)=Г₀

|| Г₀||<=A₀

2) || Г₀*f(x⁽⁰⁾)||<=B₀ 3) |²f _i(x)/x_ix_j|<=C 4) Полученные постоянные удовл-ют условию: ₀=2nA₀B₀C<1

Тогда процесс Ньютона x^(р+1)=x^(р)- W^-1 (x^(p))*f(x^(p)) – сх-ся причём x*=lim_n-x^(p) ||x*-x⁽⁰⁾||<=2B₀ Под нормой матрицы поним-ся

||A||=max_i_j|a_ij|

Метод простой итерации: x^(р+1)=x^(р)- W^-1 (x^(p))*f(x^(p)) явл-ся модиф-м методом Ньютона, и соотв-но теорема о сх-ти метода простой итерации аналогична теореме сх-ти метода Ньютона.

18. Метод скорейшего спуска решения систем.

f(x)=0 / f₁(x₁…x_n)=0

\ f_n(x₁…x_n)=0

Предположим, что все f_i непрерывны, диф-мы. Рассм-м ф-ю U(x)=(f(x),f(x))= _i=1^N(f_i(x))² Очевидно, что каждое решение исходной сис-мы обращают в нуль ф-и U(x)

И наоборот те числа, кот-е обращают в нуль ф-ю U(x), явл-ся решением исходной системы. Положим, что исход-я сис-ма имеет лишь одно решение, кот-е явл-ся т. min ф-и U(x) т.о. задача свод-ся к нахож-ю точки min ф-и U(x).

Пусть х – решение системы. х⁽⁰⁾- нулевое приближение, в точкех⁽⁰⁾ проведём поверх-ть уровня U(x)=U(x⁽⁰⁾). Если нач-я точка близка к решению,то повер-ть уровня похожа на эллипсоид. Из точки х⁽⁰⁾ будем двиг-ся по нормали к повер-ти U(x)=U(x⁽⁰⁾), до тех пор пока нормаль не коснётся другой поверх-ти уровня U(x)=U(x⁽¹⁾), затем отправляясь из точки х⁽¹⁾ по нормали к поверх-ти уровня U(x)=U(x⁽¹⁾), до тех пор пока эта нормаль не коснётся поверх-ти уровня U(x)=U(x⁽²⁾)… т.д. Очевидно, что

U(x⁽⁰⁾)>…>U(x⁽ⁿ⁾), отсюда придём к точки min ф-ии U. А этот минимум явл-ся решением исходной системы.

Обозначим U=gradU=U*i/x+U*j/y+U*k/z=[U/x,…]

Из полученных треугольников ОМ₀М₁, ОМ₁М₂…М записать: x^(p+1)=x^(p)-(p) U(x^(p))

(p)- некоторый коэф-т на каждом шаге. Задача – его найти. Рассм. ф-ю Ф()=U(x^(p)- U(x^(p)) эта ф-я задаёт изменение уровня ф-и U, вдоль соот-ей нормали к поверх-ти уровня в точке х^(р). Множитель =(р) нужно выбирать таким образом чтобы ф-я Ф() имела мин. Т.е.

dФ()/d=d*U(x^(p)- U(x^(p)))/d=0 Наим-й полож-й корень есть .

Полученную систему ур-й будем решать численно, поскольку предп что  мало, то будем брать только линейные члены разложения ф-и в ряд Тейлора ( мало, ²..-> к нулю) Ф()=_i=1^N(f_ix^(p)-_pU(x^(p)))²

Ф()=_i=1^N[f_i x^(p)-*f_i(x^(p)) *U(x^(p))/x]² - разложение в ряд Тейлора до линейных членов. f_i/x=[f₁/x₁…f_n/x_n] отсюда

Ф()/=-2[f_i x^(p)-*f_i(x^(p)) *U(x^(p))/x]* f_i(x^(p)) *U(x^(p))/x=0 Выразим :

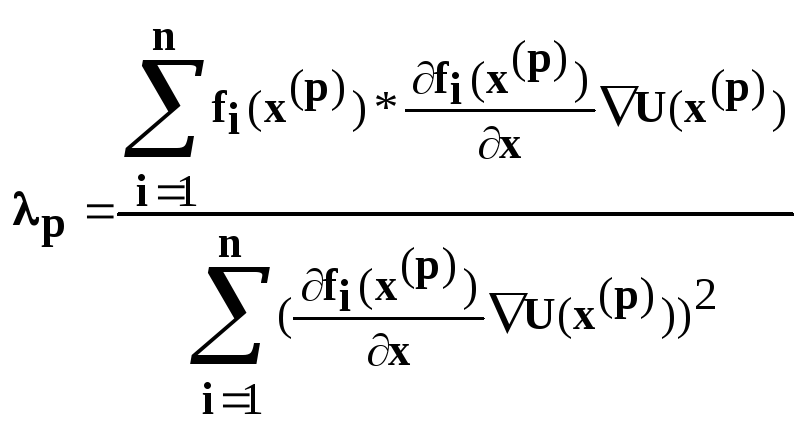
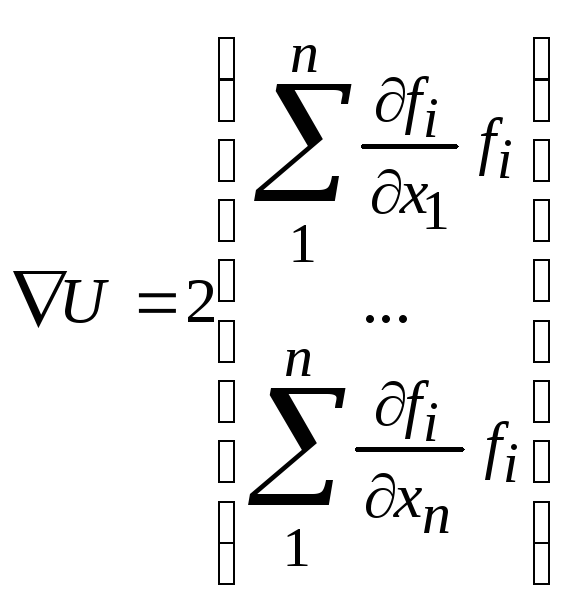
=2W^T(x)f(x); x^(p+1)=x^(p)-_pW^T(x^(p)) f(x^(p))

_p=2_р