ШПОРЫ ЭММ и М

1. Под соц.-эк. сис-мой поним. сложная вероятностная динамическая сис-ма, охват. процессы произ-ва, обмена, распред-я и потр-ия мат. и др. благ. Осн. методом исслед-ия сис-м явл. метод моделирования, т.е. способ теоретич. анализа и практич. действия, направ. на разработку и исп-е моделей. При этом под моделью поним. образ реального объекта в матер. или идеальной форме, отраж. существенные св-ва моделируемого объекта и замещающий его в ходе исслед-я и упр-я. Метод моделир-ия осн. на принципе аналогии, т.е. возм-сти изучения реаль. объекта через рассм-ние подобного ему, его модели. Важней. понятием при эк.-мат. модел-нии, явл. понятие адекватности модели, т.е. соотв. модели моделируемому объекту. Этапы эк.-мат. модел-ия:

Процесс модел-ия, включ. в себя 3 структур. элем-та: объект иссл-ия; субъект (исследователь) и модель. Выдел. след. 6 этапов: 1.Постановка эк. проблемы и ее кач. анализ. На этом этапе треб. сформулир. сущность проблемы, принимаемые предпосылки и допущения. Необходимо выдел. важней. черты и св-ва моделир. объекта, изуч. его стр-ру и взаимосвязь его элем-тов. 2.Построение мат. модели. Этот этап формализации эк. проблемы, т.е. выражения ее в виде конкрет. мат. завис-стей (ф-ий, уравнений). Построение модели подразд. в свою очередь на неск. стадий. 3.Мат. анализ модели. На этом этапе мат. приемами исслед-я выявляются общие св-ва модели и ее реш-ий. В частности, важным моментом явл. док-во сущ-я реш-я сформулированной задачи. При аналит. исслед-ии выясняется единственно ли реш-е, какие переменные могут входить в реш-е, в каких пределах они изм-ются, каковы тенденции их изм-я. 4.Подготовка исходной инф-ии. В процессе подготовки инф-ии исп. методы теории вер-стей, теоретич. и мат. статистики для орг-ии выборочных обследований, оценки достовер. данных. 5.Численное реш-е. Этот этап включ. разработку алгоритмов числен. реш-я задачи, подгот. программ на ЭВМ и непосредственное проведение расчетов. 6.Анализ численных рез-тов и их прим-е. На этом этапе реш. важней. вопрос о правильности и полноте рез-тов модел-я и применимости их как в практич. дея-сти, так и в целях усовершенствования модели. Поэтому, в первую очередь должна быть проведена проверка адекватности модели по тем св-вам, кот. выбраны в кач. существенных.

2. Теория графов – это обл. дискрет. мат., особ-тью кот. явл. геометрич. подход к изуч-ю объектов. Графы формально опис. множ. близких ситуаций. Примером служит карта автодорог, на кот. изображены перекрестки и связывающие их дороги. Перекрестки явл. вершинами графа, а дороги - его ребрами. С формал. т.з. граф предст. собой упорядоченную пару G = (V, Е) множ., первое из кот. сос-ит из вершин, или узлов, графа, а второе - из его ребер. Ребро связ. между собой 2 вершины. Граф м.б. ориентированным или нет. Ребра неориентир.графа, чаще всего наз. просто графом. В ориентир. графе ребра предст. собой упорядоч. пары вершин: 1-я вершина - это начало ребра, а вторая - его конец. Вершины изображ. кружочками, а ребра - отрезками линий. Внутри кружочков записаны метки вершин. Ребра ориентир. графа снабжены стрелками, указ. допустимое напр-е движения по ребру. Полный граф - это граф, в кот. кажд. вершина соединена со всеми ост-ми. Число ребер в полном графе без петель с N вершинами равно (N2 - N)/2. В полном ориентир. графе разреш. переход из любой вершины в любую др. Путь в графе - это послед-сть ребер, по кот. можно поочередно проходить. Путь из вершины v_i в вершину v_j это послед-сть ребер графа v_iv_i+1, v_i+1v_i+2, ..., v_j-1v_j. У всякого пути есть длина - число ребер в нем. Длина пути AB, BC, CD, DE = 4. Во взвеш. графе кажд. ребру приписано число, наз. весом ребра. При изобр. графа обычно запис. вес ребра рядом с ребром. При формал. описании вес будет дополн. эл-том неупорядоченной или упорядоченной пары вершин. Стоимость пути по взвеш. графу = сумме весов ребер пути. Кратчайш. путь во взвеш. графе - это путь с min весом, даже если число ребер в пути и можно уменьшить. Граф наз. связным, если всякую пару узлов можно соединить по крайней мере одним путем. Цикл - это путь, кот. начин. и конч. в одной и той же вершине. В ациклическом графе циклы отсут.

3. Под задачей целочис. прогр-ния поним. задача, в кот. все или некот. переменные должны принимать целые знач-я. В том случае, когда ограничения и целевая ф-ия предст. собой линейные зав-сти, задачу наз. целочис. задачей линей. прогр-ния. В противном случае, когда хотя бы одна зав-сть будет нелиней., это будет целочисл. задачей нелиней. прогр-ния. Если треб-е целочисл-сти распростр. на часть неизвестных величин задачи, то такая задача наз. частично целочисленной. Целочис. прогр-нием наз. раздел мат. прогр-ния, изуч. экстремал. задачи, в кот. на искомые переменные наклад. условие целочис-сти, а область допустимых реш-ий конечна. Огромное колич. эк. задач носит целочис. хар-р, что связано, как правило, с физ. неделимостью многих эл-тов расчета: напр., нельзя построить 2,5 завода, купить 1,5 автомобиля. В ряде случаев такие задачи реш. обычными методами, напр., симплексным методом. Однако большинство целочис. задач, таких как задача с неделимостями, принадл. к разряду так наз. трудно решаемых. Получ-е их точного реш-я не м.б. гарантировано, хотя для некот. задач дан. типа сущ. эффективные методы, позвол. находить точное реш-е даже при больших размерностях. Мат. модель задачи целочис. прогр-я представлена в виде: (2.1) f=∑ⁿ_j=1c_jx_j→max; (2.2) ∑ⁿ_j=1a_ijx_j=b_j(i=1,m‾); (2.3) x_j>=0 (j=1,n‾) - целые. Метод Гомори основан на прим-ии симплекс-метода и метода отсечения. Идея его достаточно проста и заключ. в след.: сначала находится оптималь. реш-е задачи целочис. прогр-я симплекс-методом. Если полученное реш-е целочис., то цель достигнута. Если же оптималь. реш-е не явл. целочис., то в условия задачи вводится дополнит. огр-ние, кот. отсекает от обл. допустимых реш-ий полученное нецелочис. реш-е и не отсекает от нее ни одной точки с целочис. координатами. Далее симплекс-методом реш. расширенная задача, т.е. наход. ее опорное и оптималь. реш-е. Если новое реш-е не будет целочис., то вводится еще одно дополнит. огр-ние. Процесс построения дополнит. огр-ний и реш-я задачи симплекс-методом продолж. до тех пор, пока не будет найдено оптимал. целочис. реш-е или не будет установлено, что его не сущ. Приведем алгоритм метода Гомори. 1.Симплекс-методом нах. оптимал. план задачи 2.1-2.3(таблица 2.1). Если в табл. 2.1 все свобод. члены β₁, …, β_m целые, то план (β₁, …, β_m, 0,…, 0) явл. оптимал. и для исход. задачи (2.1)–(2.4). Если задача (2.1)–(2.3) неразрешима, то и задача (2.1)–(2.4) неразрешима. Если среди свобод. членов β₁, …, β_m есть нецелые, то переходят к пункту 2 алгоритма.

2.Среди нецелых свобод. членов выбирают, напр., тот, кот. имеет наибольш. дробную часть. Пусть в нашем случае таковым явл. β_k. По строке x_jk форм. правильное отсечение в виде неравенства (2.5). {α_k,m+1}x_jm+1+{α_k,m+2}x_{jm+2+… +}{α_k,m}x_jn-x_n+1>={β_k}. 3.Неравенство (2.5) введением дополнит. неотрицат. целочис. переменной x_n+1 преобразовывают в эквивалент. ур-е {α_k,m+1}x_jm+1+{α_k,m+2}x_{jm+2+… +}{α_k,m}x_jn-x_n+1={β_k} (2.6). 4.Расширяют табл. 1 за счет включ. в нее дополнит. стро-ки для составленного ур-я (2.6) (табл. 2.2), получая тем самым симплексную табл. для расширен. задачи.

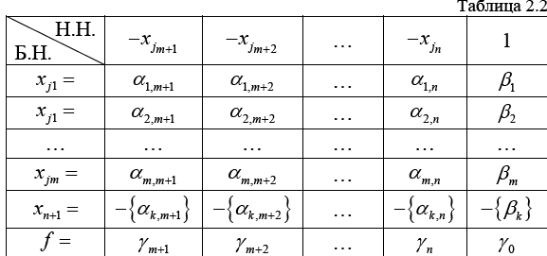
5.Составленную расширен. задачу вновь решают симплекс-методом. Если оптималь. план будет целочис., то он и станет реш-ем исход. задачи (2.1)–(2.4). В против. случае возвращ. к пункту 2 алгоритма. Если задача разрешима в целых числах, то через конеч. число итераций оптималь. целочис. план будет найден. Если в процессе реш-я появится строка с нецелым свобод. членом и целыми остальными коэффициентами, то соотв. ур-е не имеет реш-я в целых числах. В таком случае и исход. задача неразрешима в целых числах. В кач. преимуществ метода Гомори можно рассм. его эф-сть и точность, т.к. в рез-те реш-я получается наиболее оптимал. знач-е задачи. К недостаткам метода отн.: 1.трудоемкость (в некот. задачах необходимо производить множ. расчетов); 2.громоздкость (реш-е достаточно объемно, т.к. приходится искать оптимал. знач-я сначала симплекс-методом, а затем методом отс-чения, кот. также может прим. неск. раз); 3.малая применимость (метод прим. для задач с небольш. колич. переменных, т.к. при ув-чении их числа происходит значит. увелич-е трудоемкости вычислений).

4. Под задачей целочис. прогр-ния поним. задача, в кот. все или некот. переменные должны принимать целые знач-я. В том случае, когда ограничения и целевая ф-ия предст. собой линейные зав-сти, задачу наз. целочис. задачей линей. прогр-ния. В противном случае, когда хотя бы одна зав-сть будет нелиней., это будет целочисл. задачей нелиней. прогр-ния. Если треб-е целочисл-сти распростр. на часть неизвестных величин задачи, то такая задача наз. частично целочисленной. Целочис. прогр-нием наз. раздел мат. прогр-ния, изуч. экстремал. задачи, в кот. на искомые переменные наклад. условие целочис-сти, а область допустимых реш-ий конечна. Огромное колич. эк. задач носит целочис. хар-р, что связано, как правило, с физ. неделимостью многих эл-тов расчета: напр., нельзя построить 2,5 завода, купить 1,5 автомобиля. В ряде случаев такие задачи реш. обычными методами, напр., симплексным методом. Однако большинство целочис. задач, таких как задача с неделимостями, принадл. к разряду так наз. трудно решаемых. Получ-е их точного реш-я не м.б. гарантировано, хотя для некот. задач дан. типа сущ. эффективные методы, позвол. находить точное реш-е даже при больших размерностях. Мат. модель задачи целочис. прогр-я представлена в виде: (2.1) f=∑ⁿ_j=1c_jx_j→max; (2.2) ∑ⁿ_j=1a_ijx_j=b_j(i=1,m‾); (2.3) x_j>=0 (j=1,n‾) - целые. Метод ветвей и границ реш-я задач целочис. линей. прогр-я. Суть метода и технология его прим. заключ. в том, что сначала в ОДР сис-мы огр-ий 9 нах. оптим. реш-е задачи симплекс-методом без учета условия целочис. (рассм. задачу нахожд-я мах ф-ии.). Если в получ. реш-ии некот. перем. имеют дробные знач-я, то выбираем любую из дроб. переменных и по ней строим 2 огр-ия. В одном огр-нии величина переменной <= наибольш. целому числу, не превыш. знач-я дробной переменной в оптимал. реш-ии, а в др. огр-ии она >= наименьш. целому знач-ю, но не меньше знач-я дробной переменной. Если, напр., дополнит. огр-я строить по переменной x₂=9/2 (4<=9/2<=5), то первое огр-е будет x₂<=4, а второе x₂>=5, этим мы исключаем из ОДР исход. задачи промежуток с дроб. знач-ями неизвестной x₂(4<=x₂<=5).Этот промежуток разбивает ОДР θ на две части: θ1 и θ2 где 1 θ– новая ОДР, полученная добавлением к огр-ям исход. задачи дополнит. огр-я x₂<=4, а θ2– добавлением огр-я x₂>=5. В рез-те разбиения ОДР θ получены 2 новые задачи (подзадачи) линей. оптимизации. Если после их реш-я получ. знач-я неизвестных будут не целочис., то, сравнив знач-я ф-ий этих задач, выбираем задачу с больш. знач-ем ф-ии и по новой неизвестной с дроб. знач-ем строим снова два дополнит. огр-я (третье и четвертое) и разбиваем эту задачу еще на 2 новые подзадачи. Ветвление заканч. нахождением целочис. реш-я, если оно сущ. Границами в методе выст. знач-я ф-ий задач каждой ветви. На кажд. этапе реш-я задачи дальнейш. ветвлению (разбиению на новые задачи) подлежит та ветвь, у кот. знач-е ф-ии больше. Поэтому отдел. подзадачи (ветви), у кот. знач-е ф-ии меньше, м.б. отброшены. Однако иногда, сравнивая знач-я ф-ий подзадач, приход. возвращаться к ветвям, кот. ранее были отброшены, и продолжать дальнейш. реш-е от них. Поскольку множ. всех реш-ий задачи ЦЛО конечно, то после конеч. числа разбиений исход. задачи на подзадачи оптимал. реш-е будет найдено.

5. 1)Разбиваем множ. X на 2 подмнож. 1 X и 2X, находим на кажд. из них границу 1f и 2f; 2)Выбираем множ., на кот. оценка min, разбиваем его на 2 подмнож. 3X и 4X (этот процесс наз. ветвлением), находим на кажд. из них границу 3f и 4f (при этом само множ. исключ. из списка подмнож.); 3)На кажд. шаге мы имеем разбиение исход. множ. X на конеч. число подмнож. для кажд. из кот. известна граница целевой ф.ии f . Повторяем пункт 2 до тех пор, пока в каком-то из получающихся подмнож. не найдется наст. min. Такой min тоже явл. оценкой для множ., только в отличие от ост. дан. оценка явл. точной; 4)Отбрас. те подмнож. из нашего списка, граница у кот. не меньше, чем знач-е ф-ии f в найден. (.); 5)Если после этого список подмнож. окаж. пустым, найден. (.) и явл. реш-ем задачи. Если нет, продолжаем алгоритм с пункта 2, до тех пор, пока мы либо не отбросим все подмнож. как не перспективные, либо не найдем др. (.), в кот. знач-е ф-ии f еще меньше. При воплощении этого алгоритма часто исп. дерево вариантов. Вершинам дан. дерева соотв. множ. X , 1 X , 2X, …, nX и их оценки. Из кажд. вершины-множ. дуги ведут к его подмнож., получающимся при ветвлении. Если у вершины (множ.) имеется точная оценка, такую вершину помечаем звездочкой (в этой вершине далее ветвление не происх., а ее оценка исп. для прекращ. ветвления в тех вершинах, у кот. оценки больше). Примерный вид дерева вариантов представлен на рис. 4.1. Таким обр., для того, чтобы реш. задачу методом ветвей и границ, необх.:1.Предложить метод ветвления, т.е. разбиения множ. всех вариантов X на подмнож.; 2.Для кажд. из подмнож., получающ. при ветвлении указать способ для выч-ния границы (оценки целевой ф-ии на дан. подмнож.). Эф-сть прим-я метода ветвей и границ зависит от того, наск. трудоемким явл. процесс выч-ния оценок, и наск. точными явл. оценки, получаемые на кажд. шаге. Для облегчения этого процесса обычно ветвление орг. так, чтобы нах-ние оценки для всего множ. и для его подмнож. было однотипным. Желательно также, чтобы точность находимых оценок повышалась с уменьш-ем размеров подмнож. Оценить достоинства и трудности метода ветвей и границ можно только при рассм. конкрет. задач.

6. Постановка задачи о коммивояжере. Имеется n городов. Расст-я между любой парой городов известны и сос-ют a_ij(i, j=1,n‾, i≠j). Если прямого маршрута между городами i и j не сущ., то a_ij=∞. Расст-я между городами удобно запис. в виде матрицы A=(a_ij)_n×n (табл. 5.1), где a_ij=∞.

Коммивояжер, выезжая из какого-л. города, должен посетить все города, побывав в кажд. из них один, и только один раз, и вернуться в исход. город. Необх. опред. такую послед-сть объезда городов, при кот. длина маршрута была бы наименьшей.

Если городам поставить в соотв. вершины графа, а соед-щим их дорогам – дуги, то в терминах теории графов задача заключ. в опред-ии гамильтонова контура min длины. Гамильтоновым контуром наз. путь, проход. через все вершины графа, у кот. началь. вершина совпад. c конеч. Здесь под длиной контура поним. не колич. дуг, входящих в контур, а сумму их длин.

Алгоритм реш-я: 1.Приводим матрицу расс-ий по строкам и столбцам. Находим ниж. границу всего множ. маршрутов: φ(R)=γ=∑ⁿ_i=1α_i+∑ⁿ_j=1β_j. 2.Кажд. 0 в приведенной матрице условно заменяем на ∞ и находим сумму констант приведения γ_{(i, j‾)}=α_i+β_j. Знач-я γ_{(i, j‾)} запис. в соотв. клетки рядом с 0. 3.Априорно исключ. из гамильтонова контура ту дугу (i j), для кот. сумма констант приведения max искл-е дуги (i j) достиг. заменой эл-та в a_ij матрице расс-ий на ∞. В рез-те исключ-я дуги (i, j) будет образовано подмнож. гамильт. контуров {(i,j‾)}. 4.Приводим получен. матрицу расс-ий и опред. ниж. границу φ_(i,j‾) подмнож. гамильт. контуров {(i,j‾)}. 5.Априорно включ. дугу (i j) в гамильт. контур, что ведет к искл-ю в матрице, получ. после вып-я пункта 2, i-й строки j-го столбца. Замен. 1 из эл-тов матрицы на (в простейшем случае симметричный), чтобы не допустить обр-я негамильт. контура. 6.Приводим сокращен. матрицу и нах. ниж. границу φ_(i,j) подмнож. маршрутов {(i,j)}. 7.Проверяем размерность сокращен. матрицы. Если сокращен. матрица размерности 2x2, то перех. к вып-ю пункта 9; если же размерность матрицы больше, чем 2x2, то – к пункту 8. 8.Сравниваем ниж. границы подмнож. гамильт. контуров φ_(i,j) и φ_(i,j‾) и переходим к вып-ю п. 2. При этом если φ_(i,j)>φ_(i,j‾), то разбиению подлежит подмнож.{(i,j‾)} (дальнейш. анализу подверг. матрица, получ. в рез-те послед. вып-я пункта 4. Если же φ_(i,j)<φ_(i,j‾) разбиению подлежит подмнож.{(i,j)} (дальнейш. анализу подверг. матрица, получ. после послед. вып-я пункта 6. Разбиение множ. гамильт. контуров на подмнож. сопровождаем постр-ем дерева. 9.Опред. гамильт. контур и его длину. 10.Сравниваем длину получ. контура с ниж. границами оборванных ветвей. Если длина гамильт. контура не превыш. ниж. границ оборванных ветвей дерева, то задача решена. Если же длина контура больше ниж. границы некот. ветвей, то, действуя по алгоритму, развиваем эти ветви до тех пор, пока не получим маршрута с меньш. длиной или не убедимся, что его не сущ.

7. Задачи параметрич. прогр-я явл. обобщением задач линей. прогр-я. Это обобщение сос-ит в том, что данные задач параметрич. прогр-я считают не постоянными величинами, а ф-циями, определенным образом зависящими от некот. параметров. Если предположить, что произведенная пред-ем прод-ия подлежит хранению, то ее стоимость будет складываться из 2-х частей: 1)постоянной – стоимости прод-ии на момент изгот-ия; 2)переменной, завис. от срока хранения прод-ии. Мат. задачу зависимости от параметра t только коэффициентов целевой ф-ии ставят след. образом: пусть параметр t€[α;β] где и α и β – произвольные действит. числа. Необходимо найти для кажд. t на отрезке [α;β] свой вектор x‾^*=(x^*₁; …; x^*_n), маx ф-ию f_t=∑ⁿ_j=1(c_j+d_jt)x_j (1.1) при условиях: ∑ⁿ_j=1a_ijx_j<=(i=1,m‾); x_j>=0(j=1,n‾) (1.2). В выражении (1.1) числа c_j и d_j известны и постоянны. Геометрич. интерпретация задачи. Пусть сис-ма огр-ний (1.2) совместна и опред. выпуклый многогранник Ω. Ур-ию ∑ⁿ_j=1(c_j+d_jt)x_j=0 соотв. семейство гиперплоскостей, проходящих через начало координат. Отодвигая ее от начала координат в направлении возрастания ф-ии, получим реш-е в (.) A. Гиперплоскость ∑ⁿ_j=1(c_j+d_jt)x_j=0 вследствие изм-я параметра t повернется вокруг начала координат на некот. угол. Знач-е ф-ии при t=α₁ изменится, т.к. оно = взвешенному отклонению (.) A от исходной гиперплоскости. При t=α₂ гиперплоскость будет || ребру AB. Оптималь. реш-е в этом случае будет достигаться в любой (.) отрезка AB. Увеличивая t дальше (при t>α₂), получим оптимал. реш-е только в вершине B. Из постановки и геометрич. интерпретации задачи след., что при различ. знач-ях параметра t оптималь. план может оказаться не одним и тем же. Поэтому в задаче параметрич. прогр-я требуется не просто найти оптимал. реш-е, а разбить отрезок [α;β] на конеч. число интервалов, содерж. такие знач-я t, для кот. оптимал. базисное реш-е задачи достиг. в одной и той же вершине многогранника Ω. Графич. реш-е задачи. Пример. Опред. интервал изм-я параметра t и найти знач-я переменных x₁ и x₂, при кот. маx линей. ф-ии f_t=4x₁+(2+t)x₂, t€[0;8] достигается в одной и той же вершине обл. допустимых реш-ий сис-мы огр-ний: 2x₁-5x₂<=10; x₁+x₂>=5; -x₁+x₂<=4; 4x₁+5x₂<=40; x₁.=0; x₂>=0. Находим обл. допустимых реш-ий сис-мы огр-ний. Это многоугольник ABCD (рис. 7.3). Придадим параметру самое малое знач-е t=0, тогда получим ф-ию с постоян. коэффициентами f₀=4x₁+2x₂. Маx знач-е этой ф-ии достигается в вершине C.

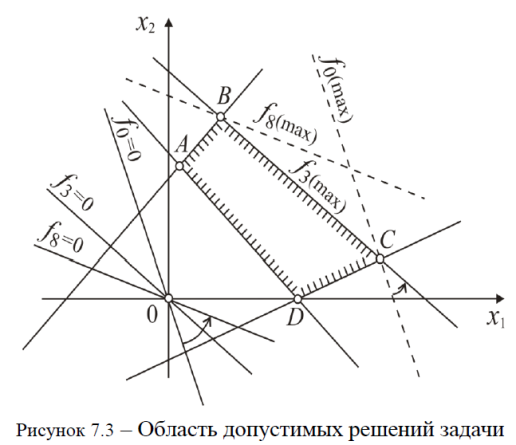
Далее приравняем f_t нулю и найдем ур-е разрешающей прямой при любом t: x₂=-4/2+t *x₁. Запишем угловой коэффициент k_f этой прямой и исследуем его поведение при изм-ии параметра t: k_f=-4/2+t. При t=0 его началь. знач-е k_f=-2. Найдем производную углового коэффициента по параметру t: (k_f)^’_t=(-4/2+t)^’_t=4/(2+t)². При любом t производная +, а угловой коэффициент при увел-нии t возрастает. Найдем предел его возрастания: lim_t→+∞k_f=lim_t→+∞(-4/2+t)=0. Т.к. при t→+∞ угловой коэффициент k_f приближается к 0 со стороны отрицат. знач-ий, то разрешающая прямая поворачивается против часовой стрелки до предель. горизонт. положения. В примере при изм-ии параметра t от 0 до некот. знач-я маx ф-ии будет в вершине C . Далее в некот. фиксир. момент времени оптимум будет достигаться на отрезке BC, а затем он перейдет в (.) B и останется в ней для всех больших знач-ий t. Опред. знач-е параметра t , при кот. реш-е задачи окажется на отрезке BC . Поскольку в этот момент прямая BC и разрешающая прямая должны быть ||, приравняем их угловые коэффициенты. Угловой коэффициент прямой BC k_BC=-4/5, след-льно, -4/2+t=-4/5, откуда t=3. Итак, при 0<=t<3 оптимал. реш-е задачи будет в вершине C(8,3;1,3), при t=3 оно достиг. на всем отрезке BC, а при 3<t<=8 в (.) B (2,2;6,2).

8. Задачи параметрич. прогр-я явл. обобщением задач линей. прогр-я. Это обобщение сос-ит в том, что данные задач параметрич. прогр-я считают не постоянными величинами, а ф-циями, определенным образом зависящими от некот. параметров. Если предположить, что произведенная пред-ем прод-ия подлежит хранению, то ее стоимость будет складываться из 2-х частей: 1)постоянной – стоимости прод-ии на момент изгот-ия; 2)переменной, завис. от срока хранения прод-ии. Мат. задачу зависимости от параметра t только коэффициентов целевой ф-ии ставят след. образом: пусть параметр t€[α;β] где и α и β – произвольные действит. числа. Необходимо найти для кажд. t на отрезке [α;β] свой вектор x‾^*=(x^*₁; …; x^*_n), маx ф-ию f_t=∑ⁿ_j=1(c_j+d_jt)x_j (1.1) при условиях: ∑ⁿ_j=1a_ijx_j<=(i=1,m‾); x_j>=0(j=1,n‾) (1.2). В выражении (1.1) числа c_j и d_j известны и постоянны. Геометрич. интерпретация задачи. Пусть сис-ма огр-ний (1.2) совместна и опред. выпуклый многогранник Ω. Ур-ию ∑ⁿ_j=1(c_j+d_jt)x_j=0 соотв. семейство гиперплоскостей, проходящих через начало координат. Отодвигая ее от начала координат в направлении возрастания ф-ии, получим реш-е в (.) A. Гиперплоскость ∑ⁿ_j=1(c_j+d_jt)x_j=0 вследствие изм-я параметра t повернется вокруг начала координат на некот. угол. Знач-е ф-ии при t=α₁ изменится, т.к. оно = взвешенному отклонению (.) A от исходной гиперплоскости. При t=α₂ гиперплоскость будет || ребру AB. Оптималь. реш-е в этом случае будет достигаться в любой (.) отрезка AB. Увеличивая t дальше (при t>α₂), получим оптимал. реш-е только в вершине B. Из постановки и геометрич. интерпретации задачи след., что при различ. знач-ях параметра t оптималь. план может оказаться не одним и тем же. Поэтому в задаче параметрич. прогр-я требуется не просто найти оптимал. реш-е, а разбить отрезок [α;β] на конеч. число интервалов, содерж. такие знач-я t, для кот. оптимал. базисное реш-е задачи достиг. в одной и той же вершине многогранника Ω.

Алгоритм реш-я задачи c вопроса №7 сос-ит из 2-х этапов: I.Параметру t дают фиксированное знач-е, напрю t= . Этим задача приводится к задаче линейю прогр-я. Решая эту задачу симплекс-методом, находят вершину, в котю f _t достигает мах. II.Определяют интервал изм-ий параметра t , для кот. маx f_t достигается в одной и той же вершине многогранника  . Найденный интервал исключают из отрезка [;]. Для оставшейся части отрезка снова решают задачу симплекс-методом, т.е. переходят к этапу I. Решение продолжается до тех пор, пока весь отрезок [;] не будет разбит на частичные интервалы.

9. Игра - упрощенная модель конфлик. ситуации. Суть игры в том, что кажд. из ее участников принимает такие реш-я, кот. могут обеспечить ему наилучший рез-т. Исход игры – это знач-е некот. ф-ии, наз. ф-ией выигрыша. Эта ф-ия задается либо таблицей, либо аналит. выражением. Если сумма выигрышей игроков =0, то игру наз. игрой с нулевой суммой. Игры, в кот. оба участника, действуя в строгом соотв. с правилами, в равной мере сознательно стремятся добиться наилуч. для себя рез-та, наз. стратегическими. В эк. практике приходится моделир. ситуации, придавая им игровую схему, в кот. 1 из участников безразличен к рез-ту игры. Такие игры наз. играми с природой. Пусть игроки и располагают конеч. числом возмож. действий – чистых стратегий. Обознач. их соотв. А_1..,А_m и В_1.., Вn. Игрок А может выбирать любую чистую стратегию А_i (i=1,m ), в ответ на кот. игрок B может выбрать любую свою чистую стратегию B_j (j=1,n ). Если игра сос-ит только из личных ходов пары стратегий (A_i,B_j) однозначно определяет рез-т a_ij – выигрыш игрока A. При этом проигрыш игрока B сос-ет a_ij. Если известны знач-я a_ij – выигрыша для кажд. пары (A_i,B_j) чистых стратегий, можно составить матрицу выигрышей игрока A (проигрышей игрока B) (табл.1). Ее наз. платежной.

Таб.1 . В таб.1 приведены числа a_i – мin возможный выигрыш игрока A, прим. стратегию А_i (i=1,m ), B_J= max a_ij – маx возможный проигрыш игрока B, если он польз. стратегией B_j (j=1,n ). Число α=max α_ij=max min a_ij, наз. нижней чистой ценой игры (максимином), а соотв. ему чистую стратегию –A⁰_i – максиминной. Число α показ., какой мin гарантированный выигрыш может получить игрок A, правильно применяя свои чистые стратегии при любых действиях игрока B. Число наз. верхней чистой ценой игры (минимаксом), а соотв. чистую стратегию B⁰_j – минимаксной. Число β=min β_ij=min max a_ij показ., какой мin гарантир. проигрыш м.б. у игрока B при правил. выборе им своих чистых стратегий независимо от действий игрока A. Правильно исп-я свои чистые стратегии, игрок A обеспечит себе выигрыш не меньше, а игрок B в рез-те правилю прим-я своих чистых стратегий не позволит игроку A выиграть больше, чем β. Ясно, что α<=β. Если α=β, то говорят, что игра имеет седловую (.) в чистых стратегиях и чистую цену игры ν=α=β. Пару чистых стратегий A_i и B_j, соотв. α и β, наз. седловой (.) матричной игры, а эл-т a_i*j* платежной матрицы, стоящий на пересечении i*-й строки и j*-гo столбца, – седловым эл-том платежной матрицы. Он одноврем. явл. мin в своей строке и маx в своем столбце, т.е. a_ij*<=a_i*j*<=a_i*j. Стратегии A_i* и B_j*, образующие седловую точку, явл. оптимальными. Тройку {A_i,B_j,ν} наз. решением игры. Для игр без седловых точек оптимал. стратегии игроков находятся в обл. смешю стратегий.