Вопрос 5. Задача о кратчайшем маршруте и метод ее решения.

Пусть задана сеть G(V, E), в которой приписанные ее дугам значения – это расстояния между вершинами, образующими эту дугу. То есть – расстояние между вершинами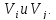 Требуется найти кратчайший путь от источникав сток .

Составим математическую модель задачи.

Что нам необходимо найти? Список дуг образующих кратчайший путь . Целевые переменные обозначим– наличие или отсутствие дугив оптимальном пути.

Целевая функция, подлежащая оптимизации – минимизация общей длины пути

Запишем ограничения задачи:

Выполнение этого ограничения гарантирует, что путь начнется в вершине и завершится в вершине.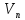

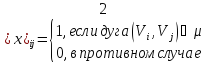
Это ограничение логически вытекает из смыслового наполнения целевых переменных.

Данная задача является задачей линейного программирования. Составим двойственную к ней, руководствуясь следующими правилами:

1. Число переменных двойственной задачи равно количеству ограничений прямой задачи.

2. Правые части ограничений прямой задачи становятся коэффициентами в целевой функции соответствующих целевых переменных двойственной задачи; а коэффициенты в целевой функции целевых переменных становятся правыми частями ограничений в двойственной задаче.

3. Смысл экстремума целевой функции двойственной задачи меняется на противоположный по смыслу прямой задачи.

4. Матрица коэффициентов системы ограничений транспонируется.

5. Если на i-ую переменную прямой задачи наложено условие неотрицательности, то i-е условие системы ограничений двойственной задачи является неравенством, если не наложено – строгим равенством.

6. Если в прямой задаче имеются ограничения равенства, то на соответствующие переменные двойственной задачи не накладывается условие неотрицательности.

Получим задачу:

Все двойственные переменные не ограничены по знаку и имеют такой смысл: (– наименьшее расстояние из вершиныв вершину .

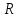
Рассмотрим алгоритм отыскания значений двойственных переменных. Обозначим через – множество помеченных вершин сети, а через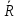– множество непомеченных

Предварительный шаг:

Помечаем источник () числом

Основной шаг:

1)Находим дуги, начальные вершины которых , а конечные. Для каждой из этих дуг определяем величину, где– пометки вершин.

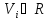Находим значение и выделяем дуги, на которых достигается этот минимум. Вершинам, являющимся конечными вершинами выделенных дуг, припишем значение, и включим данные вершины во множество.

2. Проверяем выполнимость условия для всех дуг сети, оба конца которых принадлежат. Если для какой-то дуги это условие не выполняется, то соответствующее значениезаменяем на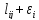. Дугу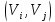выделяем и переходим к пункту 1). Пометку вершин продолжаем до тех пор, пока не будет помечен сток. На длину кратчайшего пути от источника к стоку укажет значение.

Заключительный шаг:

Оптимальный путь или пути (если их несколько), определяем, двигаясь по выделенным дугам от стока к источникув направлении, обратном их ориентации. При этом в путь включаются те дуги, для которых

.

Алгоритм сходится за конечное число шагов при условии, что сумма длин дуг любого контура, содержащегося в сети, неотрицательна.

Пример 4: Найти кратчайший путь на сети, изображенной на рисунке 6, из вершины в вершину .

Рисунок 6

1. Помечаем источник

2. 

;

. Значит, помечаем значением

И теперь множество (

Для дуги условиевыполняется.

3. 

. Значит, помечаем значением

И теперь множество (

Для дуг из множества (условиевыполняется.

4. 

.

Значит, помечаем значением

И теперь множество

(

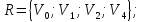
Условие выполняется для всех дуг из множества (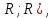кроме:. Поэтому исправляем отметку вершины

5. 

.

Значит, помечаем значением

И теперь множество

(

Для дуг из множества (условиевыполняется.

6. 

Помечаем сток значением.

Рисунок 7

На заключительном шаге находим оптимальный путь. При этом в него включаем только те дуги , для которых выполняется условие

Так как , то– последняя дуга искомого пути. Продолжая, находим 2 кратчайших пути: