Вопросы по физике к экзамену.

Первый семестр. Поток ИТ3.

Механика. Термодинамика и статистическая физика.

Часть I. Механика.

1. Механическое движение – перемещение в пространстве.

2. Система отсчета - это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точекили тел. Система координат — 4 точки, не лежащие в одной плоскости. Одна и них принимается за начало координат. Радиус вектор -  вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки, называемой началом координат. Орты – единичные  вектора, длины которых равны единице.

3. Система СИ -  система единиц физических величин, современный вариант метрической системы. Основные механические единицы — длина, масса, время.

4. Материальная точка — объект, размеры которого малы по сравнению с размерами системы, а форма не влияет на характер движения.

5. Средняя и мгновенная скорости. Средняя скорость - грубая характеристика движения. Она становится точнее, если уменьшать . Если рассматривать предел отношения при , то есть заменить отношение производной, то можно ввести мгновенную скорость в момент времени t: , где подразумевается, что орт не зависит от времени. и мгновенная скорости

6. Среднее и мгновенное ускорения - Ускорение – это скорость изменения скорости, то есть мгновенное ускорение определяется первой производной (по времени) скорости, или, что то же самое, второй производной радиус-вектора.

7. Импульс - векторная величина, полученная при перемножении массы точки на её мгновенную скорость: . Сила - векторная величина. Её обычно обозначают как . В классической механике силу связывают с изменением импульса: .

8. Энергия — способность системы совершать работу. Кинетическая - энергия механической системы, зависящая от скоростей движения её точек. Потенциальная - величина, показывающая, какую работу может совершить механическая система. Полная механическая энергия — сумма кинетической и потенциальной энергий.

9. Состояние механической системы. Механическая система обладает определённым числом   степеней свободы, а её состояние описывается с помощью обобщённых координат   и соответствующих им обобщённых импульсов  . .

10. Число степеней свободы - это совокупность независимых координат перемещения и/или вращения, полностью определяющая положение системы или тела (а вместе с их производными по времени — соответствующими скоростями - полностью определяющая состояние механической системы или тела - то есть их положение и движение). Это фундаментальное понятие применяется в теоретической механике, теории механизмов и машин, машиностроении, авиации и теории летательных аппаратов, робототехнике и других областях.

11. Основная задача механики — научиться предсказывать состояние системы в будущем.

12. Закон Всемирного тяготения — один из законов Ньютона .

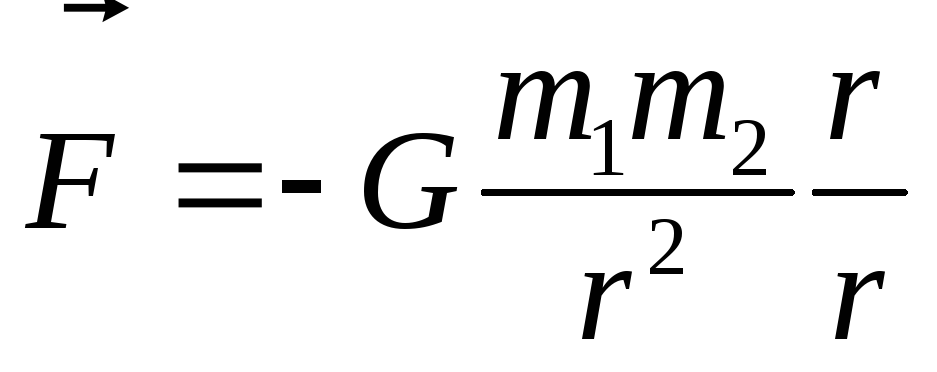13. Физический смысл Первого закона Ньютона - если результирующая всех сил, действующих на материальную точку, равна нулю, то материальная точка находится в состоянии покоя или равномерного прямолинейного движения.

14. Три формы записи Второго закона Ньютона: 1) , 2) , 3)

15. Решение основной задачи механики «в квадратурах»: . Роль начальных условий - первая задача динамики (для любого случая – прямолинейного движения или вращения, отдельной материальной точки, системы точек или твердого тела) может быть решена только при указании начальных условий.

16. Третий закон Ньютона - Пусть система состоит из двух материальных точек. Тогда можно показать (или принять как экспериментальный факт), что эти силы имеют три особенности. Они:

А) равны по величине (по модулю),

Б) направлены вдоль прямой, соединяющей материальные точки,

В) причем в противоположные стороны.

Это словесная формулировка Третьего закона Ньютона. В виде формулы этот закон записывается так:

,

индекс показывает, что рассматривается сила, действующая на первую материальную точку со стороны второй точки.

Если система состоит из материальных точек, то третий закон Ньютона обобщается:

.

Здесь есть некая тонкость, заключающаяся в том, что в механике рассматривают только парные взаимодействия частиц. Например, силы типа и более сложные не рассматриваются.

17. Плоское криволинейное движение. Простейший случай такого движения – движение по окружности или, в более общем случае – по плоской кривой. Кривая называется плоской, если все её точки лежат в одной плоскости. Как легко заметить, орты координат при этом изменяют своё направление, то есть зависят от времени.

18. Нормальное ускорение: и тангенциальное ускорение: . Их физический смысл: тангенциальное ускорение учитывает поворот касательного орта (для движения по прямой тангенциальное ускорение равно нулю). Ускорение центростремительное учитывает изменение модуля скорости.

19. Закон сохранения импульса - , Полный импульс замкнутой системы материальных точек не зависит от времени, то есть сохраняется.

20. Центр масс. Пусть есть система материальных точек с массами имеющими координаты . Тогда точка с координатами ,где называется полной массой системы, называется центром массы системы. Теорема о движении и центра масс: Центр массы системы движется как материальная точка массы М. на которую действует результирующая сила всех внешних сил. Если эта результирующая сила равна нулю, то полный импульс системы постоянен во времени.

21. Элементарная работа: Если сила непостоянна по времени или направлению, то надо брать очень маленькие перемещения , на протяжении которых сила не меняется. Тогда можно ввести понятие элементарной работы, , или, в более общем виде , – элементарное (бесконечно малое) а значит – прямолинейное смещение. Работа произвольной силы при произвольном перемещении по прямой L от начальной точки а до конечной точки в равна определенному интегралу .

22. Понятия «консервативная» и «неконсервативная» силы. Примеры: консервативные:  сила тяжести, сила упругости; неконсервативные:  сила трения и сила сопротивления среды.

23. Потенциальная энергия (материальная точка в поле тяжести и на пружине): Пусть материальная точка массой m находится на высоте h над горизонтальной поверхностью. Тогда говорят, что её потенциальная энергия равна , где g – ускорение свободного падения при данных условиях. При этом мы могли бы проводить отсчет «высоты», скажем, от потолка комнаты. Независимо от этого и вне зависимости от вида траектории, по которой падает материальная точка (свободное падение, без трения), работа совершаемая силой тяжести одинакова и равна .

Подобным же образом потенциальной энергией обладает материальная точка на пружине, жесткость которой равна k. В самом деле, при небольших растяжениях пружины , где – длина недеформированной пружины можно записать силу Гука

.

Если пружину растягивать (заметим, что перемещения конца пружины противоположно по направлению действующей силы, что приводит к замене знака « – » на знак «+» ), то совершаемая над пружиной работа, равная запасенной потенциальной энергии, составит

.

24. Закон сохранения механической энергии - если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком .

25. Всеобщий закон сохранения энергии - энергия не исчезает «в никуда» и не появляется «из ничего».

26. Принцип относительности Галилея: рассмотрим две произвольные инерциальные системы отсчета. Это означает, что системы либо покоятся относительно друг друга, либо движутся по отношению друг к другу равномерно и прямолинейно со скоростью . Говорят, что время и координаты в этих системах отсчета связаны соотношением Галилея: , .

Здесь и – радиус-векторы материальной точки в первой и второй системах отсчета, проведен из начала первой системы отсчета в начало второй системы в начальный момент движения. Второе соотношение означает, что время течет во всех инерциальных системах одинаково.

27. Принцип относительности Эйнштейна — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.

28. Преобразования Лоренца - релятивистские формулы, приводящие к инвариантности интервала, называются преобразованиями Лоренца. Они указывают, как перейти от координат инерциальной системы отсчета (включая время), которая движется со скоростью v вдоль положительного направления оси х.

Преобразования имеют вид (– скорость света в вакууме),

,

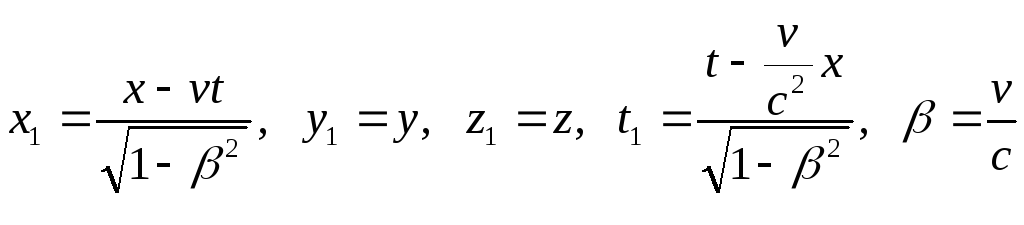Указанные преобразования симметричны:

.

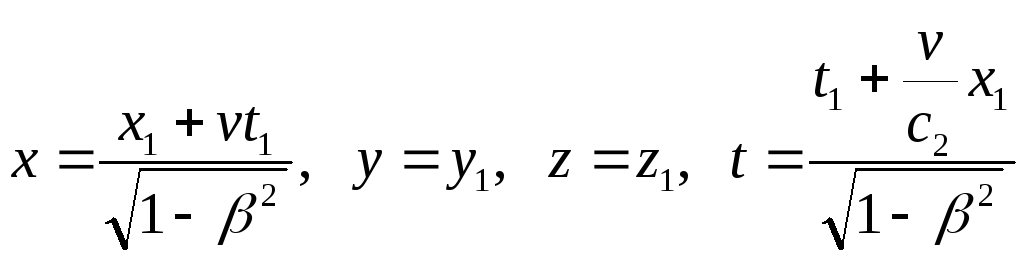29. Материальная точка на пружине как пример гармонического осциллятора.

30. Уравнение движения гармонического осциллятора: , его решение . Параметры осциллятора.

31. Слабозатухающий осциллятор с вязким трением. Уравнение движения. Реальные механические системы всегда обладают хотя бы малым трением. Простейший случай – жидкое или вязкое трение. Это трение, величина которого пропорциональна скорости движения системы (и направлена, естественно, против направления движения). Если движение происходит вдоль оси Х , то уравнение движения может быть записано (для грузика на пружинке) в виде

,

где – коэффициент вязкого трения.

Это уравнение движения можно преобразовать к виду

.

Здесь – коэффициент затухания, – по-прежнему собственная частота осциллятора (который уже нельзя назвать гармоническим; это затухающий осциллятор с вязким трением).

32. Закон движения затухающего осциллятора. 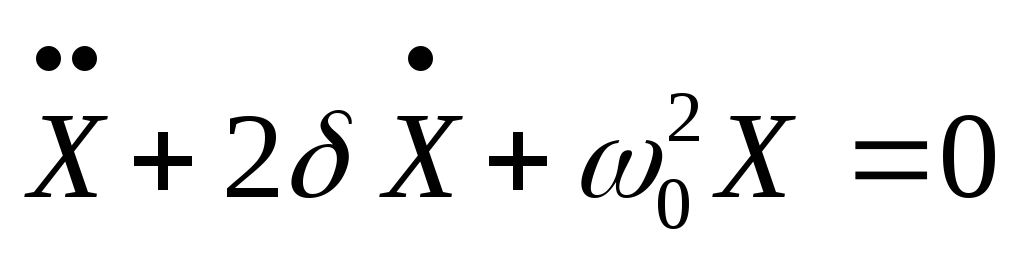Параметры затухания: Здесь – коэффициент затухания, – по-прежнему собственная частота осциллятора.

33. Вынужденные колебания. .

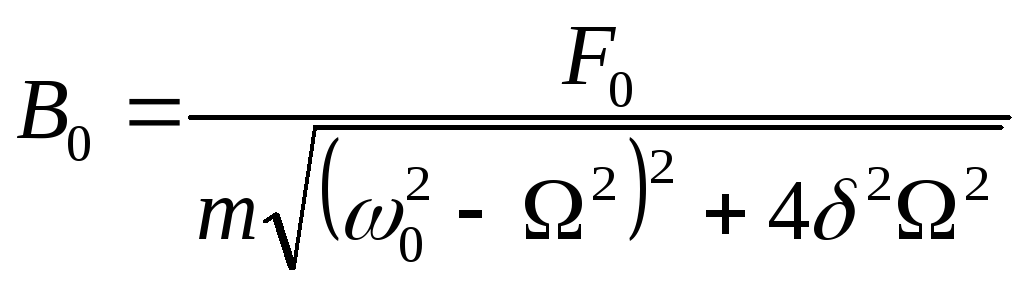Амплитуда вынужденных колебаний, а фаза вынужденных колебаний . Резонанс: при приближении собственной частоты к частоте вынуждающей силы амплитуда вынужденных колебаний возрастает.

34. Момент инерции материальной точки , системы точек, твердого тела . Роль оси. Как и масса, момент инерции это скалярная и аддитивная величина. Но она не имеет смысла, если не указана ось, относительно которой определяется этот момент.

35. Понятие абсолютно твердого тела. Адитивность моментов инерции. Кроме материальной точки и системы материальных точек в классической механике рассматривают твердые тела. Как правили, в этом случае выделение отдельных материальных точек не производят. Твердое тело рассматривают как единое целое. Естественно, что для его описания вводят новые понятия. Например, вместо массы надо рассматривать момент инерции. Как и масса, момент инерции это скалярная и аддитивная величина. Но она не имеет смысла, если не указана ось, относительно которой определяется этот момент.

36. Моменты инерции обруча, диска, стержня. Найдем найти моменты инерции некоторых твердых тел Например, момент инерции обруча, радиус которого равен , а масса равна , относительно оси, перпендикулярной плоскости обруча и проходящей через его центр, равен (в силу того, что все элементы обруча находятся на одинаковых расстояниях от оси и могут рассматриваться как материальные точки) величине

.

Эта же формула определяет момент инерции пустотелого цилиндра относительно оси его симметрии.

Приведет два примера вычисления моментов инерции более сложных твердых тел.

1. Сплошной диск или сплошной цилиндр. Ось по-прежнему перпендикулярна плоскости диска и проходит через его центр.

Выделим коаксиальное кольцо радиусом и толщиной . Площадь кольца равна и на него приходится масса

.

Соответственно этому, момент инерции выделенного кольца равен

.

Полный момент инерции диска получим, проведя интегрирование по от нуля до . После интегрирования и сокращения на множитель , результатом является

.

В силу симметрии этот же результат пригоден для сплошного цилиндра любой длины, относительно оси, совпадающей с осью цилиндра.