Метод итераций (повторений)

Пусть М – некоторое множество (значения должны быть допустимы ), Р подмножество М, где Р – множество решений. При этом х  Р  p(х)=истина. Пусть Т некоторое преобразование из М\Р в М, т.е. Т:М\РМ.

Метод итераций (дословно – повторений) состоит в том, что строится некоторое преобразование (отображение) Т:М\РМ и это преобразование последовательно применяется, начиная с какого-то х0M:

X1=T(x0), x2=T(x1), …, xn=T(xn-1), …

до тех пор, пока мы впервые не получим xi такое, что p(xi)=истина (естественно, должна быть уверенность, что рано или поздно такое xi найдется).

Напишем программу, находящую х. Пусть х0М (некоторая точка М) – начальное значение.

x :=х0; {хМ}

while not p(x) do

begin

{xM\P}

x :=T(x);

{xM}

end;

{xP}

Для корректности данной программы необходимо и достаточно доказать, что цикл завершится за конечное число шагов.

Иллюстрация работы программы:

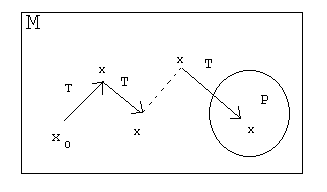
При этом множества М и Р могут быть выбраны различными способами.

Примеры:

1. Вычисление интеграла Римана

Для вычисления интеграла необходимо разбить отрезок [a,b] на р частей. При этом I_p  I, где I_p – квадратурная форма. Если увеличить количество разбиений в к раз, то получим I_pk  I. При этом если подынтегральная функция достаточно гладкая, то I - I_kp = ( I_kp - I_p )/(k^s+1-1)+o(p^-s), где s – степень точности формулы. Данная формула оценки погрешности через старший член лежит в основе метода Рунге.

При этом величина I_kp + (I_kp - I_p)/(k^s+1 - 1) будет точнее, чем I_kp. Она носит название первого шага метода Ромберга.

Рассмотрим программу вычисления интеграла.

{$N+}

Type _Real = single;

fr2r = function (x: _Real):_Real;

Function Integral (a, b: _Real; f: fr2r; eps: Real):Real;

{a, b – пределы интегрирования, f – достаточно гладкая подынтегральная функция; eps>0 – критерий Рунге. Функция возвращает приближенное значение интеграла Римана}

var

Iprev, Ipost, R: _Real;

p: word;

h: _Real;

const p0=16;

k=2;{или 3}

gamma=…..{k^s+1-1};

{далее могут следовать другие необходимые константы}

begin

if a=b then begin Integral:=0.0; exit; end;

p:=p0;

h:=(b-a)/p;

{Вычисление Ipost для числа разбиений p, а также, возможно, его частей}

R:=1e30;

While abs (R) > eps do

Begin

Iprev := Ipost;

P := p*k;

h := h/k;{p-иногда не обязателен}

{Вычисляем Ipost для p разбиений, и, возможно, его части}

R := (Ipost- Iprev)/gamma;

End;

Integral := Ipost+R;

End;

Замечания:

1. Процесс сопровождают погрешности округления. Поэтому если eps выбрать достаточно малой, то процесс зациклится.

2. Вычисление квадратурных сумм следует организовать так, чтобы погрешность была меньше. Для этого, например, суммы необходимо накапливать с более высокой точностью.

2. Вычисление функции Бесселя J₀(x) =  (-1)^k((x/2)^2k/(k!)²), где k изменяется от 0 до . С другой стороныJ₀(x)(-1)^k((x/2)^2k/(k!)²).

Данный ряд сходится к функции Бесселя при любом значении аргумента.

Суммирование производится до тех пор, пока элемент ряда не станет меньше значения погрешности, т.е. a_N <eps.

Напишем простейшую программу подсчитывающую значение функции Бесселя по ряду.

Function J0 (x, eps : _Real):_Real;

{x – аргумент функции, eps>0 – погрешность округления. Функция возвращает приближенное значение функции Бесселя}

var

k : word;

a, s : _Real;

begin

k := 0;

a :=1.0;

s := 1.0;

while abs(a) > eps do

begin

k := k + 1;

a := -a * sqr (x/2.0) / sqr (k);

s:=s+a;

end;

j0 := s;

end;

При этом k лучше было бы хранить как вещественное число.

Для увеличения скорости работы программы удобно затабулировать квадрат знаменателя. Запишем разность знаменателей на следующих один за другим шагах цикла. Z_k+1 = (k+1)²-k² = 2k + 1, в свою очередь, табулируя полученную линейную функцию, получаем U_k+1 = Z_k+1 –Z_k = 2. Таким образом нахождение k² сводится к сложению представленному следующей таблицей:

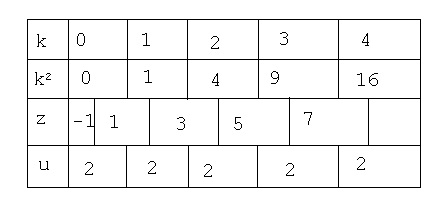
Теперь мы можем написать подпрограмму, которая будет несравненно лучше предыдущей.

Type _Real = single;

Function J0 (x, eps : _Real) : _Real;

{x – значение аргумента, eps>0 – погрешность округления. Функция возвращает приближенное значение функции Бесселя}

const u : _Real = 2.0;

var

s, a, z, z0, r : _Real;

begin

a := 1.0;

s := a;

z := -1.0;

z0 := 0.0;

r := -sqr (x/2.0);

while abs (a) > eps do

begin

z := z + u;

z0 := z0 + z;

a := a*r/z0;

s:=s+a;

end;

J0 := s;

end;

Математические свойства данной программы будут те же, т.к. используется тот же математический аппарат.

Функция Бесселя, вычисляемая в данной программе характеризуется следующими графиками :

maxa_k  ((x/2)^2[x/2]/([x/2]!)²)

maxa_k  ^1-t maxa_k, где t – длина мантиссы,  - основание системы счисления принятой в компьютере.

Таким образом, не следует брать слишком маленькие значения eps. Минимальное значение eps зависит от х и возрастает с ростом модуля х.

Из всего вышесказанного можно сделать вывод, что метод рядов Тейлора хотя и является хорошим математическим аппаратом для исследований, но не приспособлен для вычислений, т.к. область его применения ограничивается небольшой окрестностью точки разложения (в данном случае точки 0).