Простейшие приемы анализа погрешностей.

Под погрешностью понимается некоторая величина, характеризующая точность результата. Существует три вида погрешностей:

1. неустранимая погрешность (возникающая из-за неточности исходной информации);

2. погрешность метода;

3. погрешность вычислений (возникающая из-за округлений).

В процессе проведения вычислений погрешности округления могут накапливаться, так как выполнение каждой из четырех арифметических операций вносит некоторую погрешность. Например:

Относительная оценка погрешности одиночного сложения:

_xy<=x/(xy)*_x+y/(xy)*_y+_

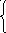
1

_<= *^1-t

1/2

(работает в области нормализованных чисел), где  - основание системы счисления принятой в компьютере, t – длинна мантиссы.

Относительная оценка результата одиночного умножения:

_x*/y<_x++_*/

Машинное представление каждого числа х можно охарактеризовать двумя величинами:

1) Абсолютная погрешность: _x= x’ – x, где x’ – приближенное значение x.

2) Относительная погрешность: _x= (_x/x) ( или (_x/x’))

_x= (_x/x’)= (_x/(x+_x)) = (_x/x)*(1/(1+(_x/x))) = (_x/x)*(1-(_x/x)+ +(_x/x)²-…) = (_x/x) + O((_x/x)²)  (_x/x). При этом с точностью до линейных членов величины равны .

Докажем написанные ранее формулы.

_x-y=_x+_y+ _-;  _-- погрешность округления;

_x-y = (_x-y/(x-y))=(x*_x)/((x-y)*x)-(y*_y)/((x-y)*y)+ ( _-/(x-y))=

=(x/(x-y))*_x+(y/(x-y))*_y+_-;

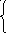
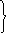
1

_-<= 1/2 *^1-t

_x/y = x’/y’ - x/y+ _/ = (x/y)((1+_x)/(1+_y)-x/y + _/

_x/y =(_x/y/(x/y))= (1+_x)/(1+_y)-1 +_/ = (1-_x)(1-_y+_y²-_y³+…)-1 +_/ =

= _x-_y+_/ +O( ²)  _x-_y+_/

Формулы погрешности при сложении и умножении доказываются аналогично.

Таким образом для оценки погрешности основных арифметических операций получаем следующие формулы:

_xy  (x/(xy))*_x(y/(xy))*_y+_;

_x/y  _x-_y+_/;

_x*y  _x+_y+_*;

_x  (1/2)*_x+_;

Рассмотрим случай непарного сложения: z = x₁+x+₂…+x_n. Накопление погрешности удобно изобразить следующим графом.

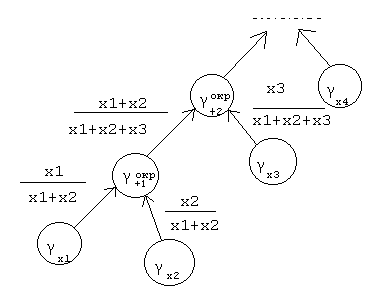
Где _x1,_x2,_x3,… - относительные погрешности соответствующих слагаемых, ₊₁,₊₂,₊₃,₊₄, … - относительные погрешности машинного представления парных сумм. При этом наглядно видно, что при увеличении числа слагаемых погрешности увеличиваются, так как идет суммирование произведений погрешностей ( они записаны возле стрелок) вдоль каждой ветви графа.

_z  (x₁/z)*_x1+(x₂/z)*_x2+ … + (x_n/z)*_xn +((x₁+x₂)/z)*₊₁+

+((x₁+x₂+x₃)/z)*₊₂+ … + ((x₁+x₂+ … +x_n)/z)*_+n-2 + _+n-1.

Если необходимо вывести детерминированную оценку, т.е. погрешность не может превзойти данной величины:

_zx₁/z*_x1+…+x_n/z*_xn+{(x₁+x₂)/z+ … +

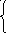
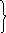1

+ (x₁+x₂+ … +x_n)/z}* *^1-t1 +

1/2

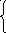
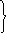1

+ *^1-t2

1/2

Причем величина погрешности существенным образом зависит от того пересылается ли промежуточное значение в память.

Если z<<x_, то _z может быть очень велика. Если промежуточная сумма x₁+…+x_k>>z_k, то влияние погрешности округления может оказаться катострофичным.

Рассмотрим для примера десятичный плавающий процессор с точностью 4 значащих десятичных цифры. Сложим 1 и 1*10^-4 (10000 раз).

Если единица прибавляется в начале

1+ 1.000*10^-4=1.0001*10⁰1.000*10⁰ и т.д. 10000 раз.

=1.

Если единицу прибавлять в конце:

1.000*10^-4+1.000*10^-4=2.000*10^-4

…

9.000*10^-4+1.000*10^-4=1.000*10^-3

…

9.999*10^-1+1.000*10^-4=10.000*10^-1=1.000*10⁰

1.000*10⁰+1.000*10⁰=2

=2.

Рассмотрим другой пример: пусть надо вычислить

Sin x=  (-1)ⁱ * X²ⁱ⁺¹/ (2i+1)! + O(X²ⁱ⁺³/(2i+3)!)

i=1..n

Формула Тейлора–Маклорена

В случае когдаХ<= O(1)- результат достаточно точен.

Напротив в случае когда Х>> O(20)-результат ложен.

То есть можно сделать вывод, что аксиоматика компьютерных арифметических операций отличается от соответствующих операций математических.

АДРЕСА

Каждая ячейка памяти имеет адрес, который используется для ее нахождения. Адреса - это числа, начиная с нуля для первой ячейки увеличивающиеся по направлению к последней ячейке памяти. Поскольку адреса - это те же числа, компьютер может использовать арифметические

операции для вычисления адресов памяти.

Если в ЭВМ используется память большого размера, тогда для ссылок на ее ячейки приходится использовать "длинные" адреса (т.е. большие по размеру), а поскольку эти адреса указываются в командах, то эти команды оказываются "длинными" (речь, конечно же, идет о машинных командах). Это плохо, т.к. увеличиваются размеры машинных программ. Сократить размеры команд при "длинных" адресах можно, например, так. Любой адрес А можно представить в виде суммы B+D, где В - начальный адрес (база) того участка (сегмента) памяти, в котором находиться ячейка А, а D - это смещение, адрес ячейки А, отсчитанной от начала этого сегмента (от В). Если сегменты памяти небольшие, тогда и величина D будет небольшой, поэтому большая часть "длинного" адреса А будет сосредоточена в базе В. Этим и можно воспользоваться: если в команде надо указать адрес А, тогда "упрятываем" базу В в какой-нибудь регистр, а в команде вместо А указываем этот регистр и смещение D. Поскольку для записи D нужно меньше места, чем для адреса А, то тем самым уменьшается размер команды. С другой стороны, благодаря модификации адресов данная команда будет работать с адресом, равным сумме D и содержимого регистра, т.е. с нужным нам адресом А. Рассмотренный способ задания адресов в командах называется сегментированием адресов.

Далее рассматривается работа процессоров Intel *8086 при формировании физического адреса в реальном режиме работы. При этом следует учитывать, что работа других процессоров может происходить по-другому, но общий алгоритм работы скорее всего такой же. Однако следует учесть, что работа процессоров в защищенном режиме резко отличается от приведенного ниже.

Большая часть арифметических операций, которые может выполнять микропроцессор 8088, ограничивается манипуляцией с 16-разрядными числами, что дает диапазон значений от 0 до 65.535 или 64 Кбайта. Поскольку полный адрес должен состоять из 20 разрядов, необходимо было разработать способ управления 20 разрядами. Решение было найдено путем использования принципа сегментированной адресации.

Если взять 16-ти разрядное число и добавить к нему в конце четыре двоичных нуля, то получится 20-ти разрядное число, которое может использоваться как адрес. Добавлением четырех нулей или сдвиг числа влево на четыре разряда фактически означает умножение числа на 16 и теперь диапазон значений будет составлять 1.024 Кбайт. К сожалению, число с четырьмя нулями в конце может адресовать только одну из 16 ячеек памяти - ту, адрес которой оканчивается на четыре нуля. Все остальные ячейки, адреса которых оканчиваются на любую из остальных 16 комбинаций из четырех бит, не могут быть адресованы при таком методе адресации. Для окончательного решения проблемы 20-разрядной адресации используются два 16-разрядных числа. Считается, что одно из них имеет еще четыре нуля в конце (выходящие за пределы разрядной сетки). Такое как бы 20-разрядное число называется сегментной частью адреса. Второе шестнадцатеричное

число не сдвигается на четыре разряда и используется в своем нормальном виде. Это число называется относительной частью адреса или смещением относительно начала сегмента. Сложением этих двух чисел получают полный 20-разрядный адрес, позволяющий адресовать любую из 1.024 Кбайт ячеек памяти в адресном пространстве IBM/PC. Сегментная часть адреса задает ячейку с адресом, кратным 16, эта ячейка называется границей параграфа. Окончательное значение указывает конкретную ячейку на определенном удалении от границы параграфа.

Чтобы лучше усвоить этот момент, рассмотрим все еще раз. Полный 20-разрядный адрес задается двумя частями, каждая из которых представляет собой 16-разрядное число. Сегментная часть адреса обрабатывается так, как будто он имеет четыре дополнительных нуля в конце. Эта сегментная часть может относиться к любой части всего адресного пространства - но она может указывать только на шестнадцатеричную границу, то есть, на адрес, оканчивающийся на четыре нуля. Относительная часть адреса прибавляется к сегментной части, образуя полный адрес. Относительная часть адреса может задавать любую ячейку памяти, отстоящую от ячейки, указываемой сегментной частью, не более чем на 64 Кбайта.

После указанных выше соображений вам уже, наверное, понятно, что полный адрес можно указать в 4 байтах (как это и делается на компьютере) - эта структура называется дальним указателем. Если мы хотим хранить только смещение, то достаточно всего 2 байт - ближний указатель. Структура указателей этих типов для компьютеров Intel приведена на рисунке:

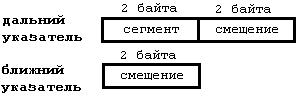
Для процессоров других фирм структура указателей может быть иной, например могут присутствовать дополнительные поля, сегмент и смещение могут иметь другие размеры.

Рассмотрим порядок формирования физического адреса в реальном режиме работы (существует еще и так называемый защищенный режим работы микропроцессора, но про него мы говорить не будем). Под физическим адресом понимается адрес памяти, выдаваемый на шину микропроцессора. Другое название - линейный адрес. Эта двойственность в названии обусловлена наличием страничной модели организации оперативной памяти.

Ее (стараничную модель) можно рассматривать как надстройку над сегментированной моделью. В случае использования этой модели оперативная память рассматривается как совокупность блоков фиксированного размера 4 Кбайт. Основное применение этой модели связано с организацией виртуальной памяти, что позволяет операционной системе использовать для работы программ пространство памяти большее, чем объем физической памяти. В страничной модели линейный адрес и физический адрес имеют разные значения. Эти названия являются синонимами только при отключении страничного преобразования адреса (в реальном режиме страничная адресация всегда отключена). Поэтому адресация происходит по следующей схеме: сначала логический адрес (записанный, например, в указателе) преобразуется в линейный адрес, а потом из линейного в физический (как вы увидели они в реальном режиме совпадают).