Метод индуктивной функции.

Введём обозначения:

А- некоторый алфавит, т. е. какое-то конечное или бесконечное множество, например множество букв русского языка или множество действительных чисел;

_k – множество конечных последовательностей длины >= к.

f : _k  Y.

Цель : подсчитать значение функции на этой последовательности.

Выделим класс функций, для которых указанная задача решается легко.

Функция f называется индуктивной, если  отображение g:Y*AY такое, что    _k  xA f(*x)=g(f(),x), где f(*x) – значение функции на последовательности расширенной на элемент x, т.е. если мы знаем значение функции на последовательности  и нам надо узнать значение на расширенной последовательности  на элемент x, то достаточно знать значение функции для  и сам элемент x.

Пусть k = 0

P.GoTop; {Встать в начало}

f := f0;{f0 – значение функции на пустой последовательности}

while not P.IsEnd do {IsEnd – означает что последовательность прочитана}

begin

P.Read(x);{или x:=P.Get;P.Skip}

f := g(f,x);

end;

{f=результат}

При k = 1.

P.GoTop;

If not P.IsEnd then

Begin

P.Read(x);

f := f({x});

while not P.IsEnd do

begin

P.Read(x);

f := g(f,x);

end;

{f=результат}

end

else … {обработка ошибки};

С ростом k текст программы существенно усложняется.

Примером индуктивной функции может служить функция нахождения максимума из последовательности чисел. Определим нашу функцию на пустой последовательности . Max{x} = x = max(max(),x). T. e.  x max()<= x . Таким образом max() = -.

P.GoTop;

Max := -;

While not P.IsEnd do

Begin

P.Read(x);

if x>max then max := x;

end;

Или в другом виде:

i := 1;

max := -32768;

while i<=n do

begin

x := a[i];

i := i+1;

if x>max then max := x;

end;

Утверждение (критерий индуктивности). F индуктивна 

 a, b : F (a) = F (b), xX выполнено F (a*x) = F (b*x) т. е. F индуктивна тогда и только тогда, когда из равенства значений F на последовательностях a и b следует равенство и на любых “одинаково удлинненных” последовательностях a*x и b*x.

Очень часто мы имеем дело с функциями которые индуктивными не являются. Это означает, что информации, заключенной в F() и х, недостаточно для вычисления F (*x). Можно, однако, посмотреть, какой именно информации нам не хватает, и рассмотреть более сложную функцию, включив в нее и эту информацию тоже. В этом случае можно использовать индуктивное расширение.

Определение. F : _k  Y_F называется игдуктивным расширением f:_k Y_f если

1. F – индуктивна;

2. Всегда значение функции f можно восстановить по F, т.е.  :Y_FY_f, такое что _k f() = (F()).

Например, нахождение номера максимального элемента последовательности не является индуктивной функцией. Индуктивное расширение:

1. номер максимального элемента на ;

2. максимальный элемент на ;

3. номер последнего элемента в .

Теорема. Для любой неиндуктивной функции существует индуктивное расширение.

Функция отображающая последовательность в себя, является универсальным индуктивным расширением для любой функции.

Определение. Пусть F₁, F₂ – два индуктивных расширения для функции f. Будем говорить, что F₁<=F₂ если существует преобразование p:Y₂Y₁ такое что  F₁() = p(F₂()).

Функция F^{^} называется минимальным индуктивным расширением функции f, если F- индуктивное расширение f.

1. F^{^}<=F

2. F^{^}(_к)=Y_F^ (если отображение «НА»)

Теорема. Для любой неиндуктивной функции существует бесконечное количество минимальных индуктивных расширений, но все они изоморфны друг другу.

Практические выводы:

1). С точки зрения информации надо программировать то минимальное индуктивное расширение время обработки которого минимально.

2). Минимальное расширение можно не использовать. Действительно, хранится лишняя информация, но если информация стоит мало памяти, а её использование существенно сокращает время основного преобразования, то есть получаем выигрыш по времени.

То есть использовать или не использовать минимальное расширение зависит от требований по времени и объему памяти в программе.

Общая схема вычисления неиндуктивной функции, с использованием индуктивного расширения.

P.GoTop;

F:=F0;{вычисление индуктивного расширения не пустой

последовательности }

while not P.IsEnd do

begin

P.read(x); {x:=P.Get;P.Skip}

F:=g(F,x) {g-преобразование, определ. в определ.

индуктивной функции}

end;

f:=(F);

Определение: Значение уY_f называется стационарным для функции f, действующей из пространства последовательности в Y_f, то есть f:Y_f , если



алфавит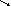

fy xA fxy

Пример Существует ли в последовательности элемент, удовлетворяющий указанному условию.

Пусть :Y; f<=<=F

y_=_(y_F)

Тогда схему можно изменить

P.GoTop;

F:=F0;

While not (P.IsEnd or stat (_(F))) do

begin

x:=P.Read;

F:=g(F,x);

end;

f:=(F);

Допустим A={( , ) + ,t}.

Рассматриваем класс произвольных формул, построенных на этом алфавите.

True False

t+t +t

(t+t)+t ( )

(t) t+t)

((t)) (t

Написать программу, осуществляющую анализ правильности формулы.

Индуктивное расширение.

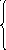
f₀()- может быть продолжено, до правильной формулы

F()= f₁()- разность числа открывающих и закрывающих скобок

f₂()- последний символ в 

Докажем, что эта функция является индуктивным расширением.

f()=истина  f₁()=0 & f₀() & (f₂())=’t’  f₂()=’)’)

f₀()=истина

f₁()= 0 ‘(’

f₂()= два решения

‘t’

Построение g

f₂(*x)=x

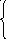x=’(’ f₁()+1

f₁(*x)= x=’)’ f₁()-1

иначе  f₁()

f₀(*x)= f₀() & (сочетание f₂() и х-правильное) & (f₁(*x)>=0)

Индуктивное расширение и формула не имеют стационарных точек.

Стационарные точки имеют f₀

Type Fch= file of char;

Function ok(var f:Fch):boolean;

{F-oткрыт для чтения; ok-возвращают правильность формулы}

var

x:char;

f0:boolean;

f1:integer;

f2:char;

begin

seek(F,0);

f0:=true;

f1:=0;

f2:=’(’;

while not(eof(F) or (not(f0)) do

begin

read(F,x);

case x of f

‘(’: f1:=f1+1;

‘)’: f1:=f1-1;

end;

f0:=(f1>=0) and Sootv(f2,x)

f2:=x;

end;

ok:=f0 and (f1=0) and ((f2=’t’) or (f2=’)’));

end;

function Sootv(a,b:char):boolean;

begin

sootV:=(((a=’(‘ )or (a=’t’)) and b=’t’) or ((a=’)’) or (a=’t’)) and (b=’t’)) or (((a=’)’) or (a=’t’)) and (b=’)’)) or (((a=’(’) or (a=’+’)) and (b=’(‘));

end;