Метод инварианта цикла.

Метод инварианта цикла является частным случаем метода итераций.

Задается некоторое множество величин М, Р М – подмножество результатов. Надо найти точку х  Р. Для этого выделим множества I M и Q M причем такие, что   I  Q  P. Таким образом, наша задача сводится к нахождению точки, которая будет принадлежать пересечению этих множеств. Причем использовать будем только такие преобразования, которые не выходят из I, то есть в нашем случае принадлежность точки множеству I является инвариантом (величиной неизменной).

Пусть x0  I – начальная точка.

Т:I\QI – преобразование инвариантно относительно принадлежности точки множеству I.

Иллюстрация к вышесказанному:

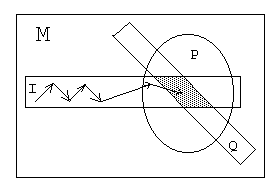
Под действием преобразования Т точка х0 переходит в некоторую точку х1, принадлежащую множеству I. Точка х1, в свою очередь, переходит в точку х2, также принадлежащую I. Этот процесс продолжается пока некоторая точка хN не перейдет в точку принадлежащую некоторому множеству Q, которое выбрано так чтобы его пересечение с I содержалось в P. Полученная точка с одной стороны принадлежит Q, а с другой принадлежит I, в силу инвариантности преобразования Т относительно I.

Схема программы:

x := x0; {xI}

while not q(x) do

begin

{x I\Q}

x := T(x);

{x  I}

end;

{x  IQ  P}

Напишем программу иллюстрирующую вышеописанный метод, которая будет обеспечивать возведенее числа в целую положительную степень.

Type _Real = single;

_Unsign = word;

function power (x : _Real; n: _Unsign ):Real;

{х - основание, n – показатель. Подпрограмма обеспечивает возведение в степень }

var z := _Real;

begin

z := 1.0;

while n > 0 do {z*xⁿ - инвариант}

begin

if odd(n) then {проверка нечетности}

begin

dec(n); {n:=n-1}

z := z*x;

end

else begin

n := n chr 1; {n := n div 2}

x := sqr(x);

end;

end;

power := z;

end;

Докажем, что данная программа завершится за конечное число шагов. Подпрограмма завершает свою работу когда z = xⁿ, т.е. пердназначена для возведения х в n – ую степень. Число повторений равно количество “0” + 2*количество “1” –1 в двоичной записи числа n <= 2*количество значащих цифр – 1 в двоичной записи = 2*]log₂n[ - 1. При этом данная программа будет очень эффективна.

Метод инвариантной функции.

Метод инвариантной функции является частным случаем метода инварианта цикла.

В данном случае х = х0 и необходимо вычислить f(x0). При этом

I = {множество x | f(x) = f(x0)}

P = {множество x | f(x) вычисляется легко}.

Построим преобразование Т – инвариантное относительно I, а в качестве условия окончания примем само значение P (Q = P).

Схема программы:

x := x0; {x  I}

while not p(x) do

begin {x  I\P}

x := T(x); {x  I}

end; {x  P  I}

result := f(x);

Для доказательства правильности достаточно доказать, что цикл выполнится за конечное число шагов.

Напишем программу иллюстрирующую данный метод.

Пусть x = (a, b), а f(x) = Н.О.Д.(a, b). Необходимо вычислить Н.О.Д.(a, b).

В данной программе будет использоваться тот факт, что делитель двух чисел

будет являться делителем их разности.

a := a0; b := b0; {>=0}

while (a>0) and (b>0) do

begin

if a>b then a := a - b

else b := b – a;

end;

result := a+b; { условием выхода из цикла является равенство 0 либо a, либо b, поэтому сумма этих чисел будет нам давать то из чисел которое не равно 0 }