
геометрия
.doc|
1
|
2.Скалярное, векторное, смешанное произведение векторов в трехмерном евклидовом пространстве. Скалярным произведением векторов и называется число равное произведению длин этих векторов на косинус угла между ними; обозначается <>=||•||•cos ; ,, *. В случае когда один вектор нулевой, косинус не определен и произведение равно 0. Скалярным произведением вектора на себя равно квадрату длины этого вектора. Осью называется прямая с зафиксированным на ней направлением. Проекцией вектора на ось ℓ называется число= произведению длины этого вектора на cos угла между вектором и осью ℓ (). Св-ва проекции вектора на ось: 1. Прℓ(+)=Прℓ+Прℓ; 2. Прℓ(α)=αПрℓ. Свойства скалярного произведения: 1. =; 2. =; 3.Скалярное произведение двух не нулевых векторов- положительно, если угол между ними острый; отрицательное, если угол между ними тупой или развернутый; и равно 0 - если векторы перпендикулярны. Геометрический смысл: =. Координатное представление скалярного произведения: пусть в пространстве задан ортонормированный базис векторов ,, =x+y+z, =x׳+y׳+z׳ <,>=xx׳+yy׳+zz׳. Следствия: 1.||2=x2+y2+z2; 2. cos =. Векторным произведением неколлинеарных векторов и , взятых в данном порядке называется вектор , длина которого численно равна площади параллелограмма, построенного на этих векторах; этот вектор перпендикулярен векторам и . Свойства: 1.=; 2.=; 3.=+. Геометрический смысл: Модуль векторного произведения векторов равен площади параллелограмма натянутого на эти вектора.=. Координатное представление векторного произведения: Если векторы и в ортонормированном правом базисе ,, имеют координаты , , то вектор имеет координаты: . Смешанным произведением некомпланарных векторов или , взятых в данном порядке, называется объем параллелепипеда, построенного на этих векторах, снабженный знаком «+», и если базис правый, и знаком «-», если этот базис левый. Свойства: 1.=; 2.=== ; 3.=; 4.=. Геометрический смысл: Смешанное произведение равно объему параллелепипеда натянутого на эти вектора.=. Координатное представление смешанного произведения: Если векторы , в ортонормированном правом базисе ,, имеют координаты , , , то ===.
|
3.Метод
координат на плоскости и с пространстве.
Формулы преобразования аффинных
координат. Координатное задание
окружности, сферы, прямой плоскости.
Суть
метода координат. Метод
координат применяется для решения
геометрических задач средствами
алгебры. Для этого вводится система
координат так, что каждой точке
сопоставляется набор чисел и наоборот.
При этом фигуры будут задаваться
аналитически: уравнениями, неравенствами
или системами. С помощью системы
координат геометрическая задача о
нахождении связей между точками и
фигурами превращается в алгебраическую
задачу о нахождении связей между
числами и уравнениями. Полученное
решение имеет определенный геометрический
смысл.
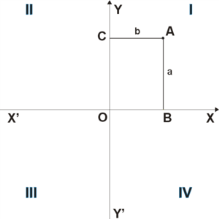
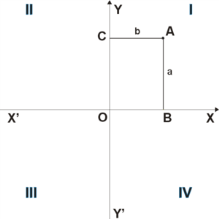
При этом координате приписывается знак минус, если точка B лежит на луче (а не на луче , как на рисунке). Координате приписывается знак минус, если точка C лежит на луче . Таким образом, и являются отрицательными направлениями осей координат. Координата называется абсциссой точки A, координата — ординатой точки A. Символически это записывают так: или или указывают принадлежность координат конкретной точке с помощью индекса: , . В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси вверх, ось смотрела направо. Обычно принято пользоваться правосторонними системами координат (если обратное не оговорено или не очевидно — например, из чертежа; иногда по каким-то соображениям бывает удобнее всё же пользоваться левосторонней системой координат). Четыре угла (I, II, III, IV), образованные осями координат и , называются координатными углами или квадрантами. Точки внутри координатного угла I имеют положительные абсциссы и ординаты. Точки внутри координатного угла II имеют отрицательные абсциссы и положительные ординаты. Точки внутри координатного угла III имеют отрицательные абсциссы и ординаты. Точки внутри координатного угла IV имеют положительные абсциссы и отрицательные ординаты.
Аффинной системой координат на плоскости (в пространстве) называется совокупность, включающая точку (начало координат) и базис направляющего векторного пространства. Точка О, – на плоскости; точка О, , – в пространстве.
Полярная
система координат на плоскости.
Возьмем на данной плоскости произвольную
точку О и назовем её полюсом. Проведем
на данной плоскости из точки О
направленный луч, который назовем
полярным лучом. Пусть М – произвольная
точка данной плоскости. Соединим точку
М с полюсом отрезком прямой
и назовем этот отрезок ОМ и его длину
Определение. Полярной системой координат на плоскости называется полюс и полярный луч вместе с понятием полярных координат любой точки плоскости. Полярная система координат в пространстве переходит в сферическую либо в цилиндрическую системы координат. Формулы преобразования аффинных координат. Рассмотрим на плоскости две аффинные системы координат и . Первую систему назовем старой, а вторую новой. Пусть М – произвольная точка плоскости, которая в старой системе имеет координаты , а в новой системе - . Задача преобразования координат состоит в следующем: зная координаты нового начала координат и новых координатных векторов в старой системе: , , выразить координаты точки М в старой системе через координаты той же точки в новой системе. По определению координат векторов и точек из , , получаем: , =, . По правилу треугольника , поэтому , или, используя равенства, =, получим: . Отсюда, учитывая, что векторы не коллинеарны, приходим к формулам: , . Так выражается координаты точки М в старой системе через её координаты в новой системе . Формулы , называются формулами преобразования аффинной системы координат. Мы замечаем, что в этих формулах матрица, составленная из коэффициентов при , есть в точности матрица перехода от базиса к базису , а свободными членами служат координаты , нового начала в старой системе . Так как векторы не коллинеарны, то , поэтому система , всегда разрешима относительно . Это позволяет выразить координаты точки М в новой системе через координаты той же точки в старой системе . Уравнение окружности . Уравнение сферы . Уравнение прямой . Уравнение плоскости .
|
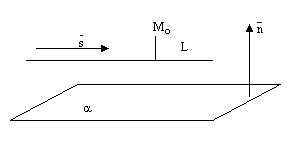
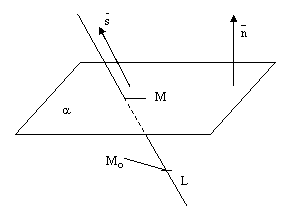
4.Исследование взаимного расположения двух плоскостей, прямой и плоскости, двух прямых в пространстве по их аналитическому заданию. Двух плоскостей: первая плоскость вторая плоскость . 1)плоскости параллельны тогда и только тогда, когда ; 2)плоскости равны тогда и только тогда, когда ; 3)плоскости перпендикулярны тогда и только тогда, когда. Прямой и плоскости: Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке,
Плоскость
2)
если
3)
если
|
|
5.
Группа движений плоскости. Классификация
движений. Движением
плоскости
называется такое отображение плоскости
в себя, при котором сохраняется
расстояние. . Множество всех движений
плоскости – группа.
Примеры
движений:
а) параллельным переносом на вектор
называется такое преобразование
плоскости, которое каждой точке x
сопоставляет точку , что вектор =; . б)
поворот вокруг точки О на угол
называется такое преобразование
плоскости, которое каждой точке М
сопоставляет точку , так что и угол
МО равен ; в) Осевой
симметрией фигуры F
с осью
называется
преобразование этой фигуры, при котором
каждой точке фигуры сопоставляется
точка, симметричная ей относительно
прямой ; (). г)
Скользящей симметрией называют
композицию
симметрии
относительно некоторой прямой
|
6.Группа преобразований подобия плоскости и её подгруппы. Свойства подобий. Преобразованием подобия называется такое преобразование плоскости, которое все расстояния меняет в одно и тоже число разложений. Это число называется коэффициентом преобразования подобия. =, , – коэффициент подобия. Пример: а) – движение – то это преобразование подобия с ; б) – гомотетия с центром в точке О и коэффициентом называется такое преобразование плоскости такое что каждой точке x сопоставляется точка так что , . Теорема о структуре (классификации) преобразований подобия. Всякое преобразование подобия с коэффициентом всегда можно представить в виде композиции движения и гомотетии – подобие – движение, – гомотетия, так что . Теорема. Если – любое подобие с коэффициентом и точка О – его неподвижная точка, то , где – либо поворот, либо осевая симметрия. Свойства преобразований подобия: 1.образом прямой является прямая; 2.образом окружности является окружность; 3.образом полуплоскости является полуплоскость. Множество всех преобразований подобия образует группу. Множество всех движений является подгруппа.
|
7.Кривые второго порядка на плоскости. Эксцентриситет, фокусы и директрисы эллипса, гиперболы, параболы. Кривой второго порядка называется множество точек на плоскости, которая в декартовой системе координат задается уравнением , где - многочлен второй степени от x,y. Примеры: , . Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек и есть величина постоянная . Каноническое уравнение эллипса +=1 это уравнение второго порядка. Эксцентриситет эллипса: 𝑒= – (а - большая полуось, в - малая, с – половина расстояния между фокусами). Директрисами эллипса называются прямые линии перпендикулярные его большей оси и удаленные от центра на расстояние – левая, – правая. Они не имеют с эллипсом общих точек. Точки и называются фокусами эллипса, а расстояние между ними – фокальным расстоянием. Гиперболой называется геометрическое место точек , разность расстояний которых до двух фиксированных точек и есть величина постоянная . Каноническое уравнение гиперболы: -=1. Эксцентриситет гиперболы: 𝑒=. Директрисы гиперболы: – левая, – правая. Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки и от данной прямой , . Точка – фокус, а прямая – директриса. Каноническое уравнение параболы: y2=2px. Теорема. Фокально-директориальная характеристика эллипса, гиперболы, параболы. 1.. 2.. 3..
|
8.Аксиоматика евклидовой геометрии. Абсолютная геометрия. Пятый постулат Евклида и его эквивалентность аксиоме параллельных. Аксиоматика Евклидовой геометрии. 1. От всякой точки до всякой точки можно провести прямую. 2. Ограниченную прямую можно непрерывно продолжать до прямой. 3. Из всякого центра всяким раствором может быть описан круг. 4. Все прямые углы равны между собой. 5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолжение неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых. Абсолютная геометрия – это часть классической геометрии, не зависимой от 5 постулата Евклидовой аксиоматики. Другими словами, это общая часть Евклидовой геометрии и геометрии Лобачевского. Пятый постулат Эвклида. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолжение неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых. Теорема: если имеет место 5 постулат, то через каждую точку М, не лежащую на прямой а, проходит только одна прямая, параллельная прямой а. Обратная теорема: если принять, что через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной, то справедлив 5 постулат.
|

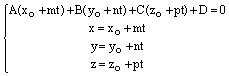
 Прямоугольная
система координат на плоскости
образуется двумя взаимно перпендикулярными
осями координат
и
(крестом).
Оси координат пересекаются в точке ,
которая называется началом
координат,
на каждой оси выбрано положительное
направление. Положение
точки A
на плоскости определяется двумя
координатами
и . Координата
равна длине отрезка , координата —
длине отрезка
в выбранных
единицах измерения. Отрезки и
определяются линиями, проведёнными
из точки A
параллельно осям
и соответственно.
Прямоугольная
система координат на плоскости
образуется двумя взаимно перпендикулярными
осями координат
и
(крестом).
Оси координат пересекаются в точке ,
которая называется началом
координат,
на каждой оси выбрано положительное
направление. Положение
точки A
на плоскости определяется двумя
координатами
и . Координата
равна длине отрезка , координата —
длине отрезка
в выбранных
единицах измерения. Отрезки и
определяются линиями, проведёнными
из точки A
параллельно осям
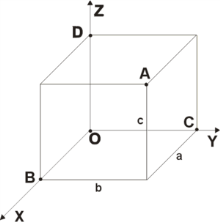
и соответственно.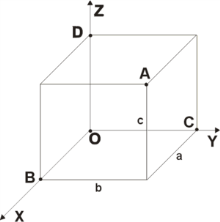 Прямоугольная
система координат в пространстве
образуется тремя взаимно перпендикулярными
осями координат , и . Оси координат
пересекаются в точке O,
которая называется началом координат,
на каждой оси выбрано положительное
направление, указанное стрелками, и
единица измерения отрезков на осях.
Единицы измерения обычно одинаковы
для всех осей. — ось
абсцисс, — ось
ординат, — ось
аппликат. Положение
точки A
в пространстве определяется тремя
координатами . Координата равна длине
отрезка OB,
координата — длине отрезка OC,
координата — длине отрезка OD
в выбранных единицах измерения. Отрезки
OB,
OC
и OD
определяются плоскостями, проведёнными
из точки A
параллельно плоскостям , и соответственно.
Координата
называется абсциссой точки A,
координата — ординатой точки A,
координата — аппликатой
точки
A.
Символически это записывают так:
или или привязывают запись координат
к конкретной точке с помощью индекса:
, , .
Прямоугольная
система координат в пространстве
образуется тремя взаимно перпендикулярными
осями координат , и . Оси координат
пересекаются в точке O,
которая называется началом координат,
на каждой оси выбрано положительное
направление, указанное стрелками, и
единица измерения отрезков на осях.
Единицы измерения обычно одинаковы
для всех осей. — ось
абсцисс, — ось
ординат, — ось
аппликат. Положение
точки A
в пространстве определяется тремя
координатами . Координата равна длине
отрезка OB,
координата — длине отрезка OC,
координата — длине отрезка OD
в выбранных единицах измерения. Отрезки
OB,
OC
и OD
определяются плоскостями, проведёнными
из точки A
параллельно плоскостям , и соответственно.
Координата
называется абсциссой точки A,
координата — ординатой точки A,
координата — аппликатой
точки
A.
Символически это записывают так:
или или привязывают запись координат
к конкретной точке с помощью индекса:
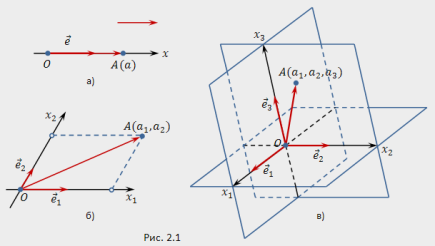
, , . Аффинные
координаты точки А (рис. б) – это
координаты вектора
в базисе, определяющей аффинную
систему. , ,
A.
Аффинные
координаты точки А (рис. б) – это
координаты вектора
в базисе, определяющей аффинную
систему. , ,
A.

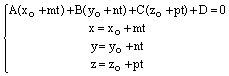 ;
(7)
;
(7)