1. Взаимное расположение прямых линий и плоскостей в трёхмерном пространстве. Для исслед. взаим. распол-я 2^-x пр-ых, прямой и пл-ти, 2^-x пл-тей в пр-ве необх. вопрос о различных способах аналит-го задания прямой и пл-ти: 1. Ур-е пл-ти

а) заданной т.M₀ (x₀,y₀,z₀) и направленным подпр-вом с базис-ми вект-ми (a₁,a₂,a₃), (b₁,b₂,b₃). Т. M(x,y,z) лежит на задан. пл-ти,↔ когда в-ра , , компланарны и  их смешанное произв-е =0. ∙ ∙ =0,

(| |=0 → в координатах)

б) задан. 3-мя точк. M₁, M₂, M₃ т.к. т. не лежат на одной прямой, то и не коллинеарны и образ-ют базис направленного подпр-ва рассм-ой пл-ти. Эту пл-ть можно опр-ть как пл-ть, проход. ч/з т.M₁ и имеющее направ-ое подпр-во L( , ), следовательно по а) ур-е будет:

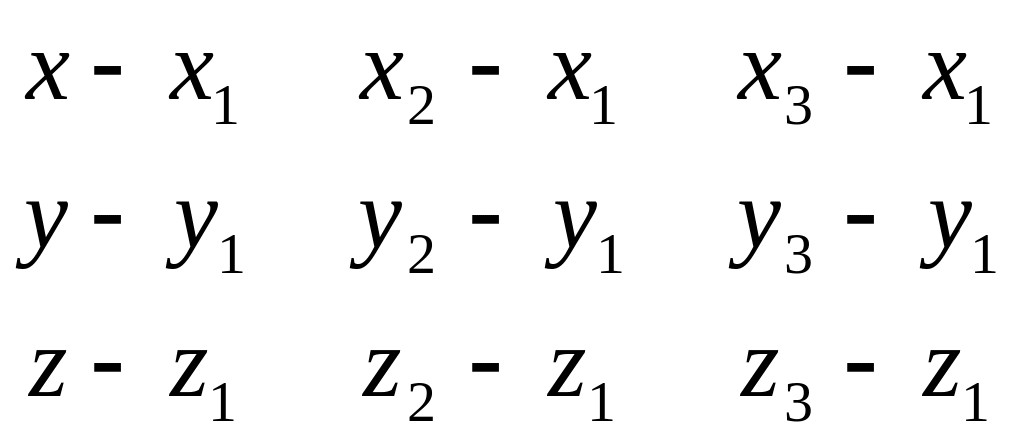| |=0

в) заданной точ. и в-ром. Опр. Гов, что в-р пл-ти γ, если в-р  век-ру из направленного подпр-ва пл-тиγ. M₀ (x₀,y₀,z₀), (A,B,C), M(x,y,z) γ↔, когда в-ры и ортогон-ны,  их скалр. произв. =0.

A(x-x₀)+B(y-y₀)+C(z-z₀)=0

г) параметрич. заданной. Пусть M₀ (x₀,y₀,z₀) γ, а L(a_ч,b_ч), (a₁,a₂,a₃), (b₁,b₂,b₃). Т. M(x,y,z) γ ↔ в-ры , , компланарны, 

=u∙ + v∙ (u,v- параметры).

x-x₀=ua₁+vb₁; y-y₀= ua₂+vb₂;

z-z₀= ua₃+vb₃

д) заданной в общем виде: Ax+By+Cz+D=0 , где D = −(Ax₀+By₀+Cz₀);

A=| |, B=−| |, C=| |.

Т. Поверх-ть в пр-ве, задан. Ур-ем 1-ой степени есть пл-ть, причем в-ры (D,-C,B), (-C,D,A), (-B,A,D) принадл-т подпр-ву этой пл-ти и к-ие-либо 2 из них преобраз-т базис этого пр-ва. Как выяснить вопрос о взаим-м распол-ии 2-х пл-ей? Задан. Тем или иным ур-ем?

γ1: A₁x+B₁y+C₁z+ D₁=0

γ2: A₂x+B₂y+C₂z+ D₂=0

r= ( ) r’=( )

Т.к. корд-ты каждой общей точки пл-тей γ1и γ2 явл. реш-ем сист. ур-ий и обратно, то вопрос о взаимном распол. 2-х пл-ей сводит. к-х пл-ей сводит.опрос о взаимном распол.инадл-т подпр-ву этой пл-ти и к-ие-либо 2 из них преобраз-т базис этого пр-ва. исслед. СЛУ

1) r’=12 ур-ия опред-ют одну и туже пл-ть (т.к. коэфф.пропорц.)

2) r’=2, r=2 различны и имеют хотя бы 1 точку (по Т Кромелера-Капелли сист. ур-ий совмест-на  r’=r) пересек. по прямой.

3) r’=2, r=1 несовм-на γ1||γ2

Если необх-мо выяснить угол м/у 2 пл-ми:

Опр. 2 пересек=ся пл-ти образ-ют 4 двугран-х угла и из этих углов наз. Угол м/у дан. пл-ми.

Cos y= =

Расстоян. м/у γ1||γ2: ρ=

λ||; λ – совм.

В исслед. взаим. распол. 3-х пл-ей ищется решение сист. Ур-ий из 3-х Ур-й. Сюда включаются случаи: имеют одну общую точку, ||-ны, пересек-ся по прямой, две пересек-ся по прямой, а 3-я совпадает с одной, попарного пересечения, две ||-ны,а 3-я их пересек-т и т.д. Исслед. в каждом из случаев м. свести к исслед. Случая располож. 2-х пл-ей.

2. Ур-ия прямой

а) каноническое. Задана т. M₀ (x₀,y₀,z₀) направлен. в-ор (p₁,p₂,p₃). M d  и коллинеар.

= = ,

если одна из корд. в-ра =0, то ур-е запиш. так = ; z-z₀=0

б) Заданы две т. M₁ и M₂, – направл. в-р (не нулевой в-р ||-ый прямой) d: = =

в) Заданы две пл-ти

γ1: A₁x+B₁y+C₁z+ D₁=0

γ2: A₂x+B₂y+C₂z+ D₂=0 и

(| |,| |,| |) – направл.в-р; ( ||γ1, ||γ2) ||d и явл. напрвл. ||γ1, т.к. p₁A₁+p₂B₁ +p₃C₁=0 ( )

г) заданы параметры x=x₀+p₁t; y=y₀+p₂t; z=z₀+p₃t; M₀(x₀,y₀,z₀) d, – направл. в-р( и коллин.→ =t ). Использ. аналог. выражение прямой, имеем: 1) ||: = , но ≠λ ≠

2) совпад. =λ =

3) пересек. ( ,[ , ])=0, ≠ (не коллинеар.)

4) скрещив. ( ,[ , ])≠ 0

3. О взаим. располож.

d: x=x₀+p₁t; y=y₀+p₂t; z=z₀+p₃t;

γ1: Ax+By+Cz+ D=0 Прямой и пл-ти. 1) прямая и пл-ть пересек-ся (имеют одну общую точку) p₁A+p₂B +p₃C≠0 ( †† ) (точ. пересеч-ия- это сист.). Угол м/у прямой и пл-ю – это угол м\у прямой и ее проекц. на эту пл-ть/

=

2) прямая || пл-ти M₀ γ, Ap₁+ Bp₂+Cp₃=0;

Ax₀+By₀+Cz₀+ D≠0

3)прямая лежит в пл-ти Ap₁+ Bp₂+Cp₃=0;

Ax₀+By₀+Cz₀+ D=0

2. Группы аффинных преобразований плоскости и пространства и их подгруппы. Признаки классификации. Применение преобразований плоскости к решению задач. Взаимосвязь движений и подобий.

Преобр-ем непустого мн-ва X н-ся всякое биективное(т.е. взаимнооднозн.) отображение f этого мн-ва на себя. Т.е. при преобр-нии элементы мн-ва x перех. в эл-ты мн-ва x.

Преобр-ие пл-сти н-ся аффинным, если оно любые 3 точки М_1, М_2, М_3, лежащие на одной прямой, перевод. в точки, лежащие на 1 прямой, и сохраняет их простое отношение, т.е. (М_1, М_2,М₃) = (М₁_, М₂_,М₃)

Лемма. Если афф. преобр-ия f1 и f2 переводят две точки А и В соотв-но в т. А и В, то f₁(M)=f₂(M), где М – люб. точка пр. АВ.

T. Пусть R=(А,В,С), R=(А,В,С)- произв.реперы пл-сти. Тогда сущ. одно и только одно афф. преоб-ие, к-ое переводит репер R в репер R. При этом любая т. М с данными корд-ми в репере R переходит в т. М с теми же корд-ми в R.

Д-во: Докажем, что  афф. преобр-ие, к-ое R→R.Построим преоб-ие f след. образом. Произв. т. М(x,y)_R поставим в соотв-ие т. М(x,y)_R. Ясно, что f явл-ся прообразом, т.к. взаимно однозначно репер R→R. (А(0,0)→А(0,0)_R, В(1,0)→В(1,0)_R, C(0,1)→C(0,1)_R). Докажем, что f-афф. прообраз. Пусть М_1,М_2,М₃- произв. точки в R с корд.(x_i,y_i), а их образы M_i(x_i,y_i)_R. Пусть (М_1, М_2,М₃)=λx_i=(x₂+x₃λ)/(1+ λ), y_i=(y₂+y₃λ)/(1+ λ). Этим рав. показано, что т. М₁ делит отрезок М₂_,М₃ в отнош. λточки леж. на одной прямой и сохр. ПОТТ. Докажем един-ость. f₁-еще одно афф. прео-ние.: R→R. Докажем, что f совпадает f₁. Пусть М-произв. т. пл-сти. Ч/з эту т. проведем прямую так, чтобы она перес. к.-н. 2 из прямых АВ, АС, ВС в разл. точках N и P. По предыд. лемме f(N)=f₁(N), f(P)=f₁(P) f(M)=f₁(M). f₁ и f совпад. f-един. отображ., которое R→R.

Изменения геом. объектов:

1. При аффин. преоб-ии всякая прямая l переходит в прямую l=f(l).

l: Ax+By+C=0. Т.к. при афф. пр-нии т. М(x,y)М(x,y), то l: . Ax+By+C=0 (ур-ие ост-ся прежним).

2. Отрезокотрезок

3. Паралл. прямаяпаралл. прямая

4. Лучлуч

5. П/пл-тьп/пл-ть

6. Реперрепер и т.д. треуг. в произв. треуг-к…

Коорд-ая характ-ка афф. преобр-ния (аналит. задание):

M(α,β)_R → M(α,β)_Rי

M´(α,β)_R´, где α´= φ(α,β),

β´= ψ(α,β).

Базис: в-ры е₁,е₂ е₁,е₂

Охар-ем репер R в репере R. Неох-мо выразить α´, β´ ч/з α,β:

В-ры ОО+ОМ=ОМ

αе₁+ βе₂=СО+ αе₁+ βе₂=α₀е₁+ β₀е₂+α (с₁₁е₁+ с₂₁е₂)+ β (с₁₂е₁+ с₂₂е₂)

αе₁+ βе₂= е₁(α₀+ αс₁₁+ β´с₁₂)+ е₂(β ₀+ α´с₂₁+ β´с₂₂)

Отсюда α= α₀+ α´с₁₁+ β´с₁₂ , β= β ₀+ α´с₂₁+ β´с_22.РИС

Основные случаи афф. пр-ний пл-сти:

1) тождеств-ое преобр-ие (реперы R и R совпадают) α= α, β=β

2) паралл-ный перенос

Вектор переноса м. опред. с пом. пары упоряд. реперов R и R с разл. началами О и О и одними и теми же коорд. в-ми е₁и е₂ (векторы ММ=а₀=ОО)

3) осевая симметрия м.б. охарактер-на 2 афф. реперами R и R=f(R)

Репер R противоп. ориентирован по отнош-ию к R

4) преобр-ие подобия также м. охаракт. с пом. 2 афф. реперов, если в качестве R выбрали ориентиров. репер, а в качестве R={0, е₁, е₂}такой что е₁е₂, а |е₁|=|е₂|=k. Тогда е₁= k е₁, е₂= kе₂

ОМ= αе₁+ βе₂= kе₁α+ kе₂β=k(е₁α+ е₂β)= k∙ОМ

5) преобр. гомотет. м.б. опис. реперами R={0, е₁, е₂}и R={0, λе₁, λе₂}. В случае λ = -1 имеет место цетр. симметрия.

6) поворот пл-сти на угол α

R = {0, е₁, е₂} е₁= е₁cosα-е₂sinα

R={0, е₁, е₂} е₂= е₁sinα+е₂cosα

1. косое сжатие плоскости

2. сдвиг плоскости

Если прямые, соед. соответсв. точки афф. пре-ия паралл. оси, то преобр-ие н-ся сдвигом пл-сти.

Утверждение. Мн-во афф. преобр-ний А образует группу.

Группой н-ся пара (с_j, 0), где с_j – непустое мн-во, на к-ом заданы бинар. операция ◦ (закон композиции) и выполн. след. аксиомы:

1. бин. операция ◦ ассоц-на

2.  ес_j: а◦е = е◦а=а

3. (ас_j) (а^-1 с_j) а◦а^-1=е

◦ - композиция y=f(x), z=g(y), то (gf)(x)=g(f(x))

C_{j E} – мн-во всех преобр. пл-сти явл-ся группой. Чтоб убед., что нек. непустое мн-во Н преобр-ний мн-ва Е явл. группой преобр-ий этого мн-ва, надо проверить выполнение 2 условий:

1. fH, gH, то f,gH

2. fH  f ^-1H

Подгруппами гр. А явл. след. мн-ва(по критерию п/гр)

1. мн-во А₁ всех афф. пр-ний 1 рода 2) гр. Р подобий 3) Д-движение 4) мн-во А(а) всех афф. пр-ний, для к-ых прямая а сост. из неподв. точек.

Классиф-ция афф. преб-ий производ. по 2 условиям:

1. опред. рода движения

Афф. пр-ие наз. преобразованием подобия 1 рода, если оно не меняет ореент. пл-сти, и 2 рода, если меняет.

2) наличие или отсутствие инвар-х элементов

x= c₁₁x+c₁₂y+x₀, y = c₂₁x+c₂₂y+y₀

а) 0 единств. инвар. точка

б) =0 x=0 y=0= одно из ур-ний системы.

в) =0 x0 y0 (нет инвар. точек)

г) 1-с₁₁=0 -с₂₁=0 x₀=0

-c₁₂=0 1-c₂₂=0 y₀=0 все точки пл-сти уд-т сист. явл. неподв. (тожд. преобр.)

Афф. пр-ие, имеющее одну неподв. точку, н-ся центро- аффинным в центре в этой точке(гомотет. поворот).

Афф. пр-ие, имеющее прямую неподв. точек, н-ся перспек-аффиным с осью – прямой неподв. точек.

10 видов афф. преоб-ий:

1) нет инв. эл-ов

2) есть 1 инв. прямая (скольз. симметр.)

3) паралл. пучок инв. прямых (паралл. перенос)

4) 1 инв. точка (поворот)

5) 1 инв. точкаединств. инв. прямой

6) 2 инв. прямые ∩ - в 1 инв. точке

7) пучок перес. инв. прямых с центром в неподв. точке (центр. симм.)

8) пучок паралл. инв. прямых и прям. инв-х точек, пересек. пучок (сжатие, осев. симм.)

9) пучок паралл. инв. прямых и прям. инв-х точек, -щих пучку (сдвиг)

10) все точки пл-сти – инв. (тожд. пр-ие)

Медианы треуг. в точке перес-ия делятся в отн-нии 2:1, считая от вершины.

Док-во: Точку перес-ия медиан М₀ выберем в к-ве центра гомотетии. Это неподв. точка афф. пре-ия. Коэфф-т гомотетии λ выберем т.о., чтобы преобр-ать любую сторону тр-ка в соотв. сред. линию. Н-р, АВ→А₀В₀. В-ор А₀В₀= λ·АВ λ=-1/2.

В-ор А₀В₀= -1/2·АВ

В-ор М₀В₀=-1/2·ВМ₀|М₀В₀|=1/2|ВМ₀| ВМ₀/ М₀В₀=1/2

Движение пл-сти – такое ее преобр-ие, кот-ое сохр-ет расст-ие м/у  2 точками.

Преобр-ие пл-сти наз-ся подобием, если оно уд-ет условию d(p(M),p(N))=kd(M,N). k>0.

x=k(xcos-εysin)tx y=k(xsin+εcos)ty

Группа афф-х преобразований пр-ва. Подгруппа движ-й. Признаки классификации. Взаимосвязь движ-я и подобия. Преобраз-я пр-ва наз-ся аффинными, если оно любые три М₁, М₂, М₃, лежацие на одной прямой, перевод-т в три точки М₁´, М₂´, М₃´, лежацие на 1 прямой, и сохр. их простое отношение.  преобраз-е подобия, в частности  движение, явл. афф-м преобраз-ем.

Как и на пл-сти, афф-е преобраз-я пр-ва переводят пл-сть (прям.) в пл-сть (прям), причем || пл-сти (|| прям.) – в || пл-сти (|| прям.). Т.к. афф-е преобр-я сохр. ПОТТ, то оно перев. отрезок в отрезок, луч в луч, полупл-сть в полуп-сть, полупр-во в полупр-во.  афф-е преобр-е либо сохр-т, либо меняет ориент-ю пр-во (I рода и II рода).

Аналитическое описание R=(O,E₁,E₂,E₃) . (x₀,y₀,z₀)

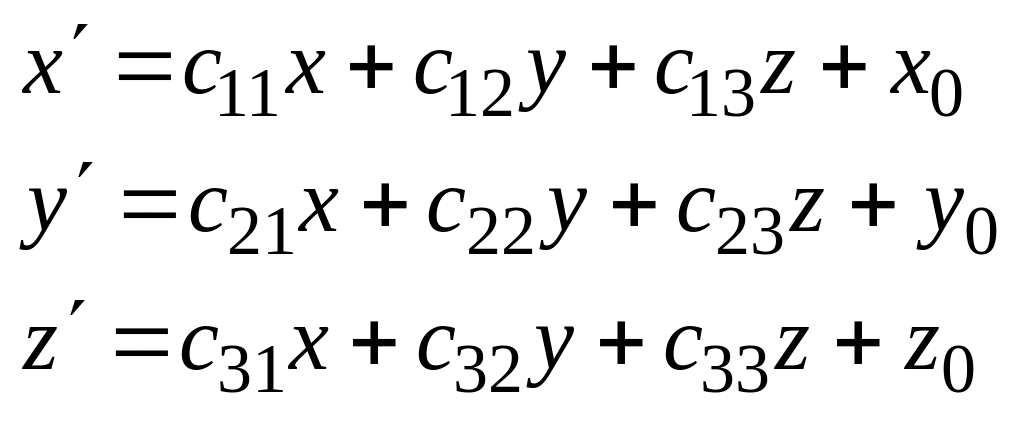
По аналогии ввод определ-е сжатия к пл-сти. ] дана пл-сть и полож-е число к. Каждой т. М пр-ва постав. в соотв. т. M` так, чтобы , где М₀ – проекция т.М на пл-сть . т. М’ пр-ва имеет только один прообраз. Т.о. построен. отображ. явл-ся преобраз-м пр-ва: оно наз.сжатием пр-ва к пл-сти . ] наз. пл-стью сжатия, к-коэф.сжатия. Все точки пл-сти ост-ся неподвиж. Если к<1, то все точки пр-ва, не лежащие на , прибл. к ней. А если к>1, то удал.(имеет место растяж.). к=1, то им. место подобие.x’=x, y’=y, z’=k*z.

Обозначим ч/з А₃ мно-во всех афф-х преоб-й пр-ва. f₁ А₃, f₂ А₃ f₁f₂ А₃. ] f А₃: А,В,С – 3 точки, лежащие на одной прямой и (АВ, С)=λ. Рассм. образы этих точек A→A’; A’=f^-1(A), B’= f^-1(B), = f^-1(C). На прямой A’B’ возьмем точку C’ так, что (A’B’,C’)= и док-м, что e’= f^-1(C). Т.к. f-афф-е преобраз-еб то (f(A’) f(B’), f(C’))=λ или (АВ, f(C’))=λ_ (АВ, С)=(АВ, f(C’))=λ _ C’= f^-1(С). Итак, мн-во А₃ всех афф-х преобр-й пр-ва образ-т группу. Она наз. группой афф-х пребраз- й пр-ва.

Рассм. важнейш. п/группы этой группы: а) ] Р₃-мн-во всех подобий пр-ва. g P₃, f P₃ fg P₃. g P₃, то g^-1 P₃ P₃ явл. группой преобр-й. Она наз. группой подобий пр-ва; б) Д₃ – мн-во всех движ-й пр-ва образ-т группу движ-й пр-ва. Эта группа явл. п/группой группы преобр-й подобий, а также п/гр. группы афф-х преобраз-й; в) мно-во всех преобраз-й I рода; г) мн-во всех парал-х переносов.

T: Преобраз-е подобия с коэф-м к>0 явл-ся композицией гомотетий с тем же коэф-м к и движения. Док-во. p=f g. Пусть М, N-точки пр-ва (пл-сти). p(M)=M’, p(N)=N’, (т.к. p-подобие).h(M)=M’, h(N)=N’’, (т.к. h-гомотетия) (т.е. сохраняет расст-е). M=h^-1(M’’), p(M)= M’’p(h^-1(M’’))=M’=p(M). Анал-но p(h^-1( ))=p(N). Преобраз-е p h^-1 сохр-т расст-е м/у двумя любыми т. M’’,N’’, т.е. явл. движением; p h^-1=f, p=f h. Чтд.

Говорят, что реперы R=(O, A, B, C) и R’=(O’, A’, B’, C’) один-во (против-но) ориент-ные базисы , , , и , , одинак-во (противоп-но) ориент-ны.

По аналогии с преобр-ем пл-ти сущ. 2 движ-я: I рода и II рода (меняющие или нет ориентацию пр-ва). Инв. точка – если при некот-м преобр-ии она перех-т в себя, прямая (пл-сть) инв – если ее образ совпадает с ней. Частным случаем инв. прям. явл-ся прямая инвар-х точек, все точки которой явл-ся инв-ми.

Классиф-я движ-й пр-ва в завис-сти от наличия инвар-х эл-ов: 1) движ-е им-т по крайней мере 3 инв-х т., не лежащие на 1 прямой. g(A)=A, g(B)=B, g(C)=C. Сущ-т единств-я пл-сть, проход-я ч/з А’, В’, С’, т.е. -инвар-я пл-сть. Пусть D→D’  AD→A’D’. а) Д=Д’. Верш. репера R={O, A, B, C}переход-т в себя. G явл-ся тожд. (т.к. по аналогии с преобраз-м пл-сти сущ-т не >1 движ-я, которое R→R’) I рода; б) Д и Д’ симм-ны отн-но пл-сти (сим.) II рода.

2) движ-е имеет по крайней мере 2 инвар-е точки А и В, но не им.инвар-х точек, не лежащих на прямой АВ  люб. точки прямой инвар.: а) поворот на угол вокруг оси АВ (I рода), б) частный случай поворота – поворот вокруг прямой на – сим-я отн-но прямой (I рода), в) =0 тождест-е преобраз-е.

3) Движ-е им. только одну инвар-ю точку. Лемма.  движ-е пр-ва имеет хотя бы инвар-ю прямую. Обозначим =(А, d); –инвар-я пл-сть. Поворотное отраж-е – композ-я поворота g₁ вокруг d на и сим-я g₂ отн-но пл-сти (II рода).

4) Движ-е не им. ни одной инвар-й точки. Лемма. Если движ-е не им. инвар-х точек, то любые 2 его инвар-е прямые парал-ны.

а) парал-ый перенос, причем инвар-я прямая явл-ся те и т. те прямые пр-ва, которые парал-ны вектору p (I рода);

б) скользящее отражение – композ-я отраж-й от пл-сти на паралл-й перенос на вектор р 0, паралл-но пл-сти. (II рода)= Iр IIр;

в) винтовое движ-е – композ-я (произв-е) поворота вокруг прямой d с углом поворота 0 на парал-й перенос на вектор р 0, вектор р парал-й d. Инвар-ы только 2 прямая d. (I рода)