motau

				Варианты практического занятия № 4 (продолжение)
	№										Задания
	вари
				1					2			3			4					5
	ри-
														a3	a3		a3	a3
	анта
		4	7	1	4	4					4	24	16
							2	0	1	0									f (x, y)
		3	0	5	7	2					1	7	1
	17.						2	1	2	1				2	1		3	5	y3	3y
		5	6 6		1 7						4	18	49
							2 1		1 1										+x2	16x 9
71		7	6	4	3	3
		0	1	0	1	0					8	16	32
							2	0	0	0									f (x, y)
		0	1	0	0	1					1	3	2
	18.						1	0	1	2				1	3		4	6	2 y3	6 y
		0 1 0			0 0						4	2	55
							2	1 1 1											+2x2	20x 1
		1	1	0	1	0
		0	1	0	1	0					6	12	24
		0	1	0	0	1	2	0	0	0									f (x, y)
	19.						1	0	1	2	1	4	22	6	8		3	1	2 y3	6 y
		0 1 0			0 0
							2	1 1 1			4	14	75						+2x2	20x 1
		1	1	0	1	0

2.ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЗВЕНЬЕВ

ИСИСТЕМ

При изучении систем автоматического управления рассматриваются динамические и статические режимы. При изучении динамических (неустановившихся) режимов математическим аппаратом является аппарат дифференциальных уравнений.

Уравнения, которые кроме неизвестной функции одной или нескольких переменных содержит также производные от этой функции, называются дифференциальными уравнениями. Если неизвестные функции зависят от одного переменного, дифференциальные уравнения называются обыкновенными, в противном случае – уравнениями в частных производных.

При построении математической модели возможно разбиение системы на отдельные звенья и их математическое описание. Совокупность уравнений отдельных звеньев и уравнений связи между ними образует систему n уравнений, описывающую систему управления в целом.

Теория матриц оказалась эффективным средством исследования и решения систем дифференциальных уравнений. Среди них наиболее простыми являются линейные дифференциальные уравнения с постоянными коэффициентами.

Линейной системой дифференциальных уравнений называется система таких уравнений, в которые неизвестные функции и их производные входят линейно.

В дальнейшем мы будем рассматривать системы уравнений первого порядка и ограничимся случаем, когда эти системы разрешены относительно производных. Такие системы называют нормальными. Линейная система имеет вид:

d x1(t)
				a11 x1(t)	a12	x2(t)	...	a1n xn(t)	g1(t)
	dt									(2.1)
									,
				.........................................................
	d xn	(t)
				an1 x1(t)	an2	x2(t)	...	ann xn	gn (t)
	dt

где x1(t), x2 (t), xn (t) – неизвестные функции от независимой переменной t, которые надо определить; a11,a12, ann – коэффициенты системы; g1(t), g2 (t), , gn (t) – функции, которые определены и непрерывны на некотором интервале (a < t < b); n – порядок системы.

72

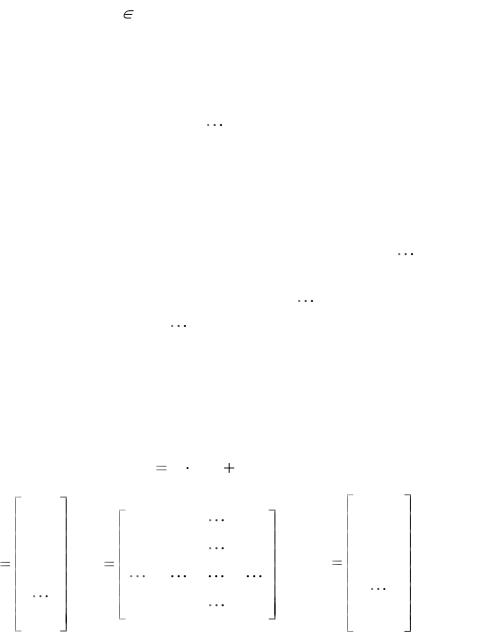
Если для любого t (a,b) функции gi (t)=0 (i=1, 2,....n ), то система дифференциальных уравнений называется однородной; в противном случае – неоднородной.

Совокупность функций:

x1(t), x2 (t), xn (t),	(2.2)
определенных и дифференцируемых на интервале (а, b),	называется
решением системы (2.1) на интервале (a ,b), если они обращают урав-

нения (2.1) в тождества, справедливые при всех значениях t из интервала (a,b). Графической интерпретацией полученного решения будет поверхность в (n+1) -мерном пространстве (t, x1(t), x2 (t), xn (t)) , назы-

ваемая интегральной.

Задача нахождения решения x1(t), x2 (t),	xn (t), удовлетворяющего
начальным условиям x10 , x20 , , xn0 при t=t0	называется задачей Коши.
Решение (2.2), в каждой точке которого имеет место существование

и единственность решения задачи Коши, называется частным решением.

Система (2.1) может быть записана в векторной форме:

			dx(t)	A x(t)	G(t) ,
			dt
	x1(t)		a11	a12	a1n
	x2 (t)
			a21	a22	a2n ;, G(t)
где x(t)	x (t) ;	A
	3
	xn (t)		an1	a21	ann

(2.3)

g1(t) g2 (t)

g3 (t) ,

gn (t)

где x(t) – вектор неизвестных функций; A – матрица коэффициентов системы; G(t) – вектор правой части системы дифференциальных уравнений.

73

2.1. РЕШЕНИЕ ОДНОРОДНОЙ СИСТЕМЫ ДИФФЕРНЦИАЛЬНЫХ УРАВНЕНИЙ

Практическое занятие № 5

Основные положения

В матричной форме однородная система дифференциальных уравнений имеет вид:

	dx(t)	A x(t) .
			(2.4)
	dt

Согласно методу Эйлера общее решение X (t) системы (2.4) в матричной форме записывается:

X (t)	Ф(t) X0 ,						(2.5)
где Ф(t) – фундаментальная матрица системы; X 0					–вектор начальных
условий.
Фундаментальную матрицу системы можно получить из следую-
щего выражения:
(t)	H (t) H	1	,				(2.6)
				e 1t	0	0
где H – модальная матрица системы;		(t)		0	e 2t	0	–
				0	0	e nt

диагональная матрица собственных значений матрицы А.

Порядок решения системы дифференциальных уравнений

1. Записываем матрицу коэффициентов системы дифференциальных уравнений:

74

	a11	a12	a1n
A	a21	a22	a2n .
	an1	a21	ann
2. Составляем характеристическое уравнение системы det ( A				E) 0 ,

где Е – единичная матрица.

3. Находим характеристические числа системы (2.4) (корни характеристического уравнения). Различают три вида корней характеристического уравнения.

Все корни i различны и вещественные.

Вектор-столбцы h(i) (i 1, 2, , n) модальной матрицы системы

H находятся из решения однородной системы алгебраических уравнений:

	( A	i E) h(i)		0 (i 1, 2, , n) .
Или в развернутом виде:
(a11	i ) hi1	a12	hi2 ...	a1n	hin	0
a21 hi1	(a22	i )	hi2 ...	a2n	hin	0	(2.7)
an1 hi1	an2	hi2	... (ann	i )	hin	0
Другим более простым вариантом					нахождения вектор-столбцов

модальной матрицы является взятие в качестве компонент вектора h(i) алгебраических дополнений элементов первой строки определителя | A E | при соответствующем численном значении i .

Среди корней характеристического уравнения имеются кратные корни.

Выделяют два случая:

a) если для корня	k	кратности к имеются m линейно независимых
собственных векторов	h(1) , h(2) , , h(m) , причем m=k, то этому корню

k соответствует решение вида:

75

	x(t)	c h(1)e kt			c		h(2)e kt	...	c h(m)e kt ,		(2.8)
		1			2				m
где c1, c2 ,	, cm – постоянные интегрирования, находящиеся из началь-
ных условий.
б) если для корня				k	кратности k имеется m линейно независимых
собственных векторов, причем m<k, то решение следует искать в
виде многочлена степени k-m, умноженного на										e kt :
x (t) P(m k ) (t)		e k t ;	x (t)			Q(m k ) (t)		e k t ;...; x (t)		S(m k ) (t) e k (2.9)
1			2						m
где P(m k ) (t), Q(m k ) (t),				, S(m k ) (t) – алгебраические полиномы с неиз-
вестными коэффициентами;							k – кратный корень.
Для	нахождения				неизвестных				коэффициентов		полиномов
P(m k ) (t), Q(m k ) (t),			, S(m k ) (t) , следует выполнить подстановку выра-

жений (2.9) в исходную систему (2.4).

Приравняв коэффициенты подобных членов в левой и правой частях уравнений, получим систему линейных алгебраических уравнений относительно искомых коэффициентов. Причем количество коэффициентов, равное кратности корня k , являются произвольными, а остальные коэффициенты выражаются через них.

Среди корней характеристического уравнения имеются комплексные корни. Для получения решения воспользуемся следующими положениями.

Если коэффициенты системы (2.4) вещественные, то решение выражается только через вещественные функции. Вещественная и мнимая

часть	комплексного				решения,	соответствующая			корню
i	(	0) , являются линейно-независимыми решениями.
Для корня			i	частное решение системы имеет вид:
	x1(t) h1 e( i )t ;				x2 (t) h2 e( i )t ; ;			xn (t) hn e( i )t .
Пусть:
x (t) Re h e(				i )t	,	x (t) Im h e(			i )t ,
11		1				21		1
. . . . . . . . . .						. . . . . . . . . . . .
			(	i )t		x	(t) Re h e(		i )t .
x1n (t) Re hn e					,	2n		n

76

Тогда решение за счет комплексных корней выразится через два найденных линейно-независимых решения:

x1(t)	c1 x11	c2 x21; x2 (t) c1 x21	c2	x22; ...;	(2.10)
xn (t)	c1 x1n	c2 x2n.
Решения, соответствующие корню			i	, будут линейно зави-

симыми, поэтому учитывать их не нужно.

Таким образом, определив для каждого корня характеристического

уравнения i соответствующие решения, как указано в пунктах1-3, и сложив их, получим общее решение системы (2.4).

Пример 1

Найти решение системы дифференциальных уравнений

dx1		4x1	8x2	x3
dt
dx2		5x1	9x2	x3
dt
dx3		4x1	6x2	x3
dt

x0,1

с начальными условиями X 0 x0,2 .

x0,3

Решение

Система однородная.

1.Составляем матрицу коэффициентов:

4 8 1

A 5 9 1 . 4 6 1

77

2.Составляем лямбда-матрицу (А- Е):

			4		8	5
( A	E)		5		9	1	.
			4		6	1
3. Составляем характеристическое					уравнение		det |А- Е |=0:
	3	6	2	11	6	0 .

4.Находим корни характеристического уравнения:

	1	1;	1	2;	1	3	(корни вещественные, разные).
5.	Собственные векторы hi						(i	1, 2, 3)	находим в виде алгебраиче-
ских дополнений элементов первой строки определителя det( A												E) :
						1,1		2	10		15
				h(i)	k	1,2		k	5	9	.
					i			i
									4	6
						1,3
6.	В последнее выражение производим подстановку численных зна-
чения		i :

1

2

3

			2		10		15		6
			1			1
	h(1)
1:		k		5	1	9		k	4	;
		1						1
				4	1	6			2
			2		10		15		1
			1			1
2 :	h(2)	k2		5 1		9		k2	1 ;
				4	1	6			2
			2		10		15		6
			1			1
3 :	h(3)	k		5	1	9		k	6	,
		3						3
				4	1	6			6

где k1, k2 , k3 – произвольные коэффициенты, не равные нулю.

78

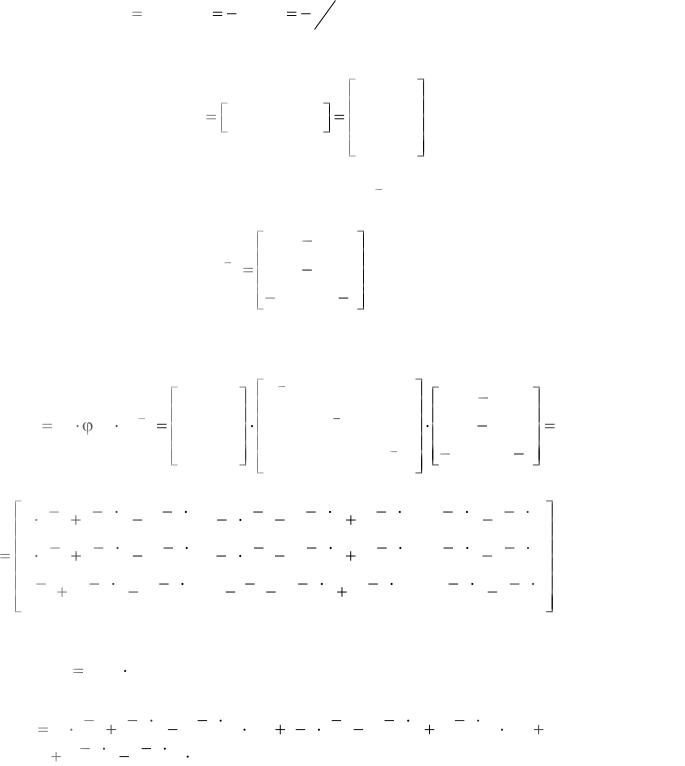
7.Принимаем ki таким образом, чтобы упростить столбцы модаль-

ной матрицы: k 0,5; k		1; k		1	.
1	2		3	6

8.С учетом этого модальная матрица запишется:

		3	1	1
H	h(1) , h(2) ,h(3)	2	1	1 .
		1	2	1

9.	Произведем расчет обратной матрицы H 1 :
				1	1	0
		H 1		1	2	1 .
				3	5	1
10.	Рассчитываем	элементы				фундаментальной				матрицы:
	3	1	1	e( 1)t		0	0	1	1 0
Ф(t) H (t) H 1 2		1	1	0	e( 2)t		0	1	2 1
	1	2	1	0		0	e( 3)t	3 5		1

3 e t	e 2 t			3e 3 t		3 e t	2e 2 t	5e 3 t	e 2 t	e 3 t
2 e t	e 2 t			3e 3 t		2 e t	2e 2 t	5e 3 t	e 2 t	e 3 t .
e t	2e 2 t			3e 3 t		e t	4e 2 t	5e 3 t	2e 2 t	e 3 t
11. Получаем				решение данной системы					согласно	выраже-
нию X (t)	Ф(t)		X0 :
x (t) (3 e t		e	2 t 3e		3 t ) x		( 3 e t	2e 2 t 5e 3 t ) x
1						01				02
(e 2		t	e	3 t ) x		;
				03

79

x (t) (2 e t			e 2 t		3e	3 t ) x		( 2 e	t	2e 2 t	5e 3 t ) x
2	2	t		3	t ) x		01				02
(e			e				;
					03
x (t) (e t		2e 2 t			3e	3 t ) x		( e t	4e	2 t 5e	3 t ) x
3	2		t	e 3 t )			01				02
(2e						x ,
						03
где x01, x02 ,			x03		– элементы вектора начальных условий.

Пример 2

Найти решение системы дифференциальных уравнений:

	dx1				4x1	2x2	5x3
	dt
		dx2			6x1	x2	6x3
		dt
	dx3				8x1	3x2	9x3
	dt
									x0,1
с начальными условиями								X 0	x0,2 .
									x0,3
								Решение
Система однородная.
1. Составляем							матрицу			коэффициентов:
								4	2	5
							A	6	1	6 .
								8	3	9
2. Составляем лямбда-матрицу ( A									E) :

		4	2	5
( A	E)	6	1	6 .
		8	3	9

80