Краткая теория

Простейшим случаем вращательного движения является вращение твердого тела вокруг неподвижной оси. При этом все точки тела описывают окружности, центры которых лежат на одной прямой, являющейся осью вращения. Вращательное движение удобно характеризовать углом поворота «», угловой скоростью «», т.к. все токи при таком вращении поворачиваются на один и тот же угол «», движутся с одинаковой угловой скоростью «».

Аналогом величин, характеризующих поступательное движение во вращательном движении вокруг неподвижной оси являются:

1) пройденный путь S - угол поворота;

2) линейная скорость =dS/dt- угловая скорость=d/dt;

3) ускорение – угловое ускорение;

4) масса тела m - момент инерцииJ вращающейся материальной точки массойmотносительно оси неподвижной оси на расстоянииr:J = mr² , а для любого тела –;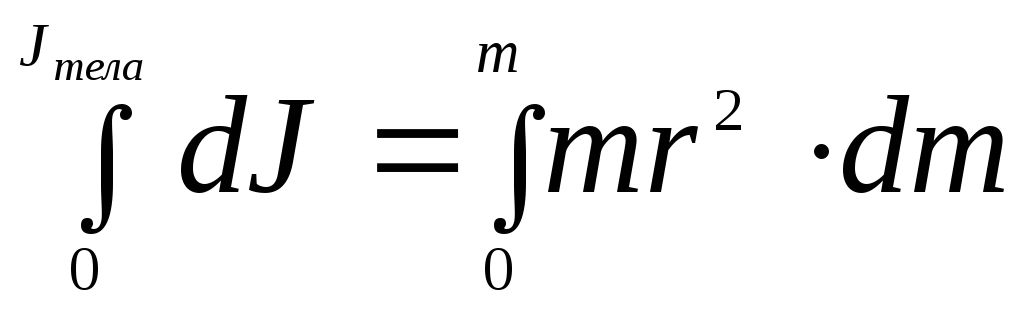

5) сила - момент силы, характеризующий вращающее действие силы;

6) импульс тела - момент импульса тела.

Рассмотрим некоторые из названных и другие величины

Угловая скорость - вектор, численно равныйd / dtи направленный по оси вращения по правилу правого винта (если рукоятку правого винта вращать по направлению вращения тела, то направление поступательного движения винта покажет направление угловой скорости). Единицей измеренияявляется []= 1 рад/с (с^-1).Если вращение происходит с постоянной угловой скоростью(=const), то =( -₀)/t, отсюда = ₀ + t.Угловую скорость можно выразить следующим образом:=2 / T = 2n, гдеn=1/T- число оборотов в секунду,Т- период вращения.

При изменении угловой скорости вводят понятие углового ускорения:

[] =1 рад/с² (1/с²).

Угловое ускорение - вектор, совпадающий по направлению с угловой скоростью при ускоренном движении и противоположной ей – при замедленном. Угловое ускорение связано с тангенциальным (касательным) ускорением:

Т.к. , то,

где - линейная скорость

Для характеристики динамики вращательного движения вводятся понятия момента силы и момента инерции.

Рассмотри движение материальной точки "А" с массойmпо окружности радиусомr(рис. 1). Пусть на точку "А" массойmдействует сила, лежащая в плоскости, перпендикулярной оси вращенияО. Тогда точка приобретает постоянное тангенциальное ускорениеа_,определяемое тангенциальной составляющей силы:

F_ = F Sin = m (1)

Так как =r.Равенство (1) можно записать следующим образом:

F Sin = mr(2)

Умножив правую и левую часть равенства (2) на rполучим:

Fr Sin = mr² или M =J , отсюда:

, (3)

где М=FrSin или в векторной форме:= [] - вращающий момент (момент силы), J=mr²- момент инерции вращения материальной точкиАмассойmотносительно оси «О».

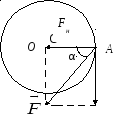
Рисунок 1. Вращение материальной точки А массой m относительно оси «О»

Зависимость является вторым законом Ньютона для вращательного движения и называетсяосновным уравнением динамики вращательного движения. Это же выражение справедливо и для характеристики вращательного движения твердого тела с учетом того, чтоJ- момент инерции тела, характеризующий его инерционное свойство во вращательном движении относительно какой-либо оси. Для определения момента инерции твердого тела необходимо разбить тело на бесконечно малые элементы с массойdm, найти моменты инерции каждого элементаdJи проинтегрировать их. Каждый элемент можно приближенно принять за материальную точкуc, тогда:

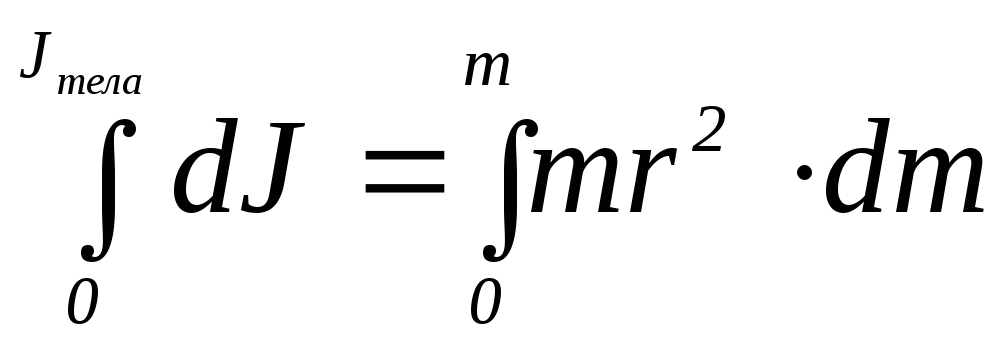или (4)

Для тел различной геометрической формы момент инерции рассчитывается по формулам, полученных при интегрировании выражения (4).

Для примера рассчитаем момент инерции однородного стержня длиной lи массойm, когда ось вращенияООпроходит через его середину

O

dx

x

x

l

O

Рисунок 2. Момент инерции тонкого прямого стержня

относительно его центральной оси, перпендикулярной к стержню

На расстоянии х от оси вращения выделяем малый участок стержня длинойdxмасса этого участка равнаdm, тогда согласно формуле (4), момент инерции для этого участка запишется в виде

Для определения dmвводим линейную плотность, как , тогда , а момент инерции

Момент инерции для всего стержня запишется в виде:

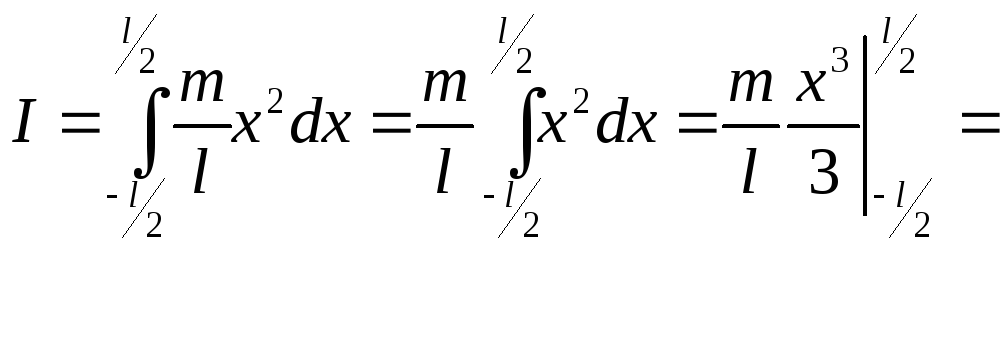
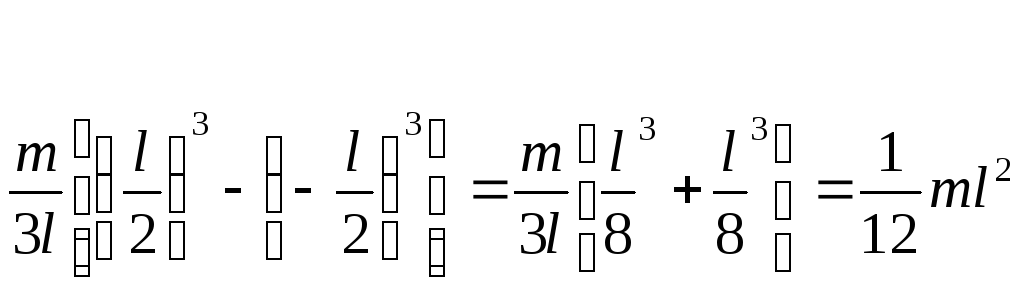
Если ось вращения тела О₁О₁параллельна оси симметрииОО, но смещена от нее на расстояниеd, то момент инерцииI,относительно новой осиО₁О₁определяется по теореме Штейнера

где I₀- момент инерции тела относительно оси симметрии. рассчитаем момент инерции для однородного тонкого стержня длинойlи массойm, когда ось вращения проходит перпендикулярно к стержню через его конец

;

тогда

O

O₁

O

O₁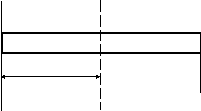

O₁

d

O

O₁

Рисунок 3. Момент инерции тонкого прямого стержня относительно оси.

Для других однородных тел геометрически правильной формы массой mотносительно оси симметрии момент инерции рассчитывается по формулам:

1) для однородного сплошного цилиндра (диска) относительно продольной осиJ=mR²/2, гдеm- масса цилиндра,R- его радиус;

2)для однородного шара радиусаR, массой m относительно оси, проходящей через его середину

3)для тонкого однородного кольца (обруча) радиусаRмассойm относительно оси, проходящей через центр перпендикулярно к плоскости кольцаJ = mR² и т.д.

Для тел геометрически неправильной формы массы mмомент инерции определяется экспериментальным путем.

Основное уравнение динамики вращательного движения тела можно записать в ином виде, учитывая, что ,или

(5)

Величина называетсяимпульсом момента сил, приложенных к телу, аd() - изменениемомента количества движениятела (момента импульсатела).

Приведенное равенство (5) показывает, что изменение момента количества движения вращающегося тела равно импульсу момента приложенных к нему сил.

Если =О, тоd()= 0 или, т.е. момент количества движения остается постоянным.

Это следствие называется законом сохранения момента количества движения: если сумма моментов сил, действующих на тело, равна нулю ( = 0), то момент импульса тела остается постоянным (= const). Например, при выполнении «сальто» в прыжке человек «группируется», прижимая голову и ноги друг к другу, тем самым снижает момент инерцииJсвоего тела; а так как= const, то угловая скорость вращения тела повышается и, следовательно, время переворота человека уменьшается.

Изучение законов вращательного движенияв лабораторной работе производится с помощьюмаятника Обербека, который представляет собой крестовину, состоящую из 4-х стержней каждый длинойl/2, прикрепленных к втулке с осью (рис.4).

На стержнях фиксируются грузы массой m₁, которые могут быть закреплены симметрично на различных расстояниях от оси вращения. На шкив радиусомr, находящийся на оси вращения, наматывается нить, к свободному концу которой прикрепляется грузР.

Если предоставить грузу Рвозможность двигаться, то это падение будет происходить с ускорениема. При этом шкив со стержнями и расположенными на них грузами будет вращаться с угловым ускорением, которое можно найти, измерив высотуhи время падения грузаt.

(6)

где r- радиус шкива, на который наматывается нить.

Силой, создающей вращающий момент, является сила натяжения нити Т. Из второго закона Ньютона для грузаРследует+=m. Переходя от векторной суммы к алгебраической, проектируя на осьОХимеем:Р - Т = ma, откуда

T = P - ma = mg - ma = m(g-a) (7)

Тогда вращающий момент

M = Tr = m(g-a)r (8)

Момент инерции маятника может быть определен из основного уравнения вращательного движения:

J=M/ (9)

Подставляя в формулу (9) формулы (5) и (7) получим окончательное выражение для момента инерции маятника Обербека, определенного практически (экспериментально):

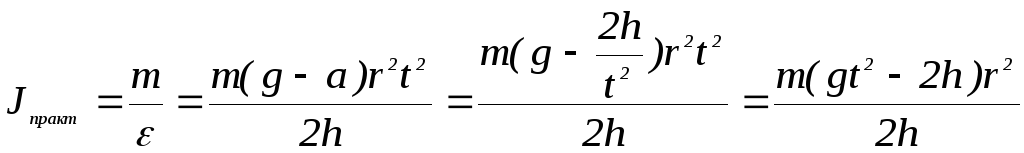. (10)

С другой стороны, теоретически, момент инерции маятника может быть найден из формулыJ_теорет J_k + 4J_rp(моментом инерции цилиндра радиусаrпренебрегаем), гдеJ_k- момент инерции крестовины,J_rр- момент инерции груза относительно оси вращения. Считая груз материальной точкой массойm₁, его момент инерции можно найти по формулеJ_rp= m₁R², гдеR- расстояние от оси вращения до центра масс груза.

Тогда момент инерции крестовины теоретически определяется по формуле:

где m₂- масса «двойного» стержня,l– его длина (см. рис.4).(11)