1 Обработка результатов измерений

1.1 Виды измерений

Измерение – это сравнение физической величины с другой, однородной, принятой за единицу измерения (эталон).

Все измерения подразделяют на два вида по способу получения значений физических величин: прямые и косвенные, и на два вида по желаемой точности: технические и лабораторные.

При прямых измерениях определяемую величину сравнивают с единицей измерения непосредственно или при помощи измерительного прибора, проградуированного в соответствующих единицах. То есть при прямом измерении значение измеряемой величины считывают непосредственно со шкалы или табло измерительного прибора. Так, например, измеряется время какого-либо процесса секундомером, длина какого-либо предмета – линейкой, скорость автомобиля – спидометром и т.д.

При косвенных измерениях искомую величину измеряют (вычисляют) по результатам прямых измерений других величин, которые связаны с измеряемой величиной определенной функциональной зависимостью. То есть при косвенном измерении измеряемую величину находят в результате вычисления по некоторой формуле, в которую входят результаты прямых измерений. Так, например, можно измерить плотность тела, зная массу и объем тела, среднюю скорость движения тела, зная путь, пройденный телом, и время, за которое этот путь пройден, и т.д.

Технические измерения – это измерения, проводимые техническими приборами с невысокой точностью. Проводят их, как правило, однократно в производственных условиях.

Лабораторные измерения – это измерения, проводимые лабораторными приборами с высокой точностью. Проводят их, как правило, многократно в исследовательских лабораториях.

1.2 Погрешности измерений

Если измерять одну и ту же физическую величину X достаточно точным прибором n раз, то получаемые значения X₁, X₂,…, X_i,…, X_n-1, X_n различаются, но группируются около некоторого среднего значения X_ср. Какое же значение будет истинным – X_ист? С чем связан разброс экспериментальных данных? Для удобства восприятия значения физической величины можно отображать на числовой оси (рисунок 1.1).

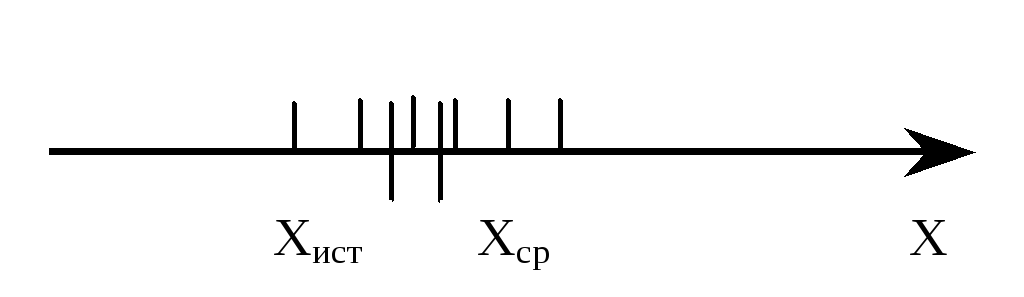
Рисунок 1.1 – Разброс значений при измерениях

Оказывается, невозможно абсолютно точно измерить величину X и получить истинное ее значение, так как этому препятствует ряд факторов.

Какие же факторы мешают измерить истинное значение и обуславливают разброс экспериментальных данных? В качестве примера рассмотрим измерение времени падения тела с некоторой постоянной высоты секундомером. В процессе измерения ”участвуют”: человек, проводящий измерения; физическое явление (падение тела с некоторой высоты под действием силы тяжести); прибор (секундомер, при помощи которого проводят измерение времени). Каждый из “участников" может внести ошибку в процесс измерения. Человек, проводящий измерения, может ошибиться при считывании значения времени с секундомера. Кроме того, у каждого человека своя реакция: с момента, когда тело упало, должно пройти некоторое время, пока человек среагирует и нажмет на кнопку остановки секундомера. Измерительный прибор всегда имеет цену деления, которая ограничивает точность измерений. Если цена деления секундомера 1 мс/дел, то при помощи него никак не измерить время с точностью до 1 мкс. Условия, при которых производится измерение, также могут внести ошибки в значение физической величины. Случайный ветер, колебания влажности и температуры воздуха могут исказить результаты измерений.

Таким образом, ошибку в измерения может внести сам экспериментатор, измерительный прибор, условия, при которых происходит измерение – само физическое явление.

Абсолютной погрешностью измерения называется разность между измеренным значением физической величины X и ее истинным значением

X = X_изм–X_ист. (1.1)

Относительной погрешностью измерения называется отношение абсолютной погрешности к истинному значению измеряемой величины

_X = X/X_ист. (1.2)

Относительная погрешность, по сути, является долей абсолютной погрешности от истинного значения измеряемой величины. Ее часто выражают в процентах, умножая выражение (1.2) на 100.

Как определить X, если истинное значение неизвестно?

В первом приближении в качестве оценки истинного значения чаще всего принимают среднее арифметическое

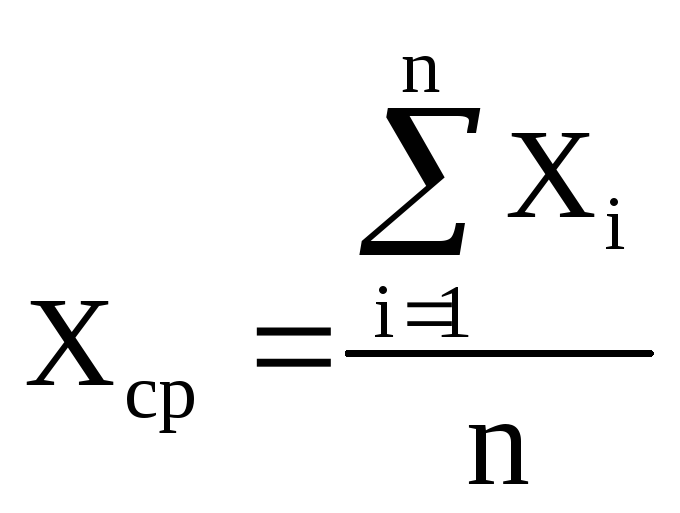. (1.3)

Тогда в качестве оценки абсолютной погрешности i-го измерения принимают величину

X_i = X_i–X_ср. (1.4)

Каждое измерение дает значение определяемой величины с некоторой погрешностью X_i. Это значит, что истинное значение лежит в интервале

X_изм – X  X_ист X_изм + X. (1.5),

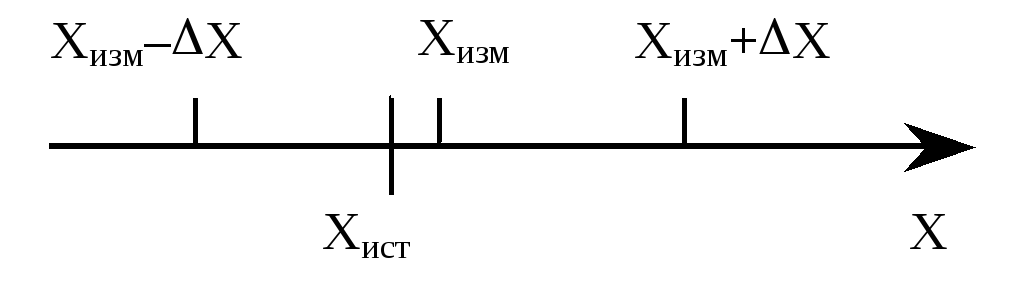
Рисунок 1.2 – Доверительный интервал

В случае, когда одно и то же измерение проводится несколько раз, в качестве погрешности принимают некоторую усредненную, по всем i-ым измерениям, оценку абсолютной погрешности.

Все погрешности подразделяют на промахи, систематические и случайные погрешности.

1. Промах – грубый просчет экспериментатора. Это чрезмерно большие ошибки, допущенные человеком, в процессе измерений. Такие ошибки могут возникнуть, например, в случае, если экспериментатор неправильно произвел отсчет значения физической величины со шкалы прибора, ошибся при записи результата измерения в таблицу экспериментальных данных. Сюда же относятся ошибки, допускаемые при вычислениях. Измерения, содержащие промахи, следует отбрасывать и проводить повторное измерение.

2. Систематические погрешности – это ошибки, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины. Систематические погрешности можно разбить на два вида – приборные (инструментальные) и методические. Методические погрешности связаны с недостатками метода измерения, с неправильной постановкой эксперимента. Например, если при вычислении дальности полета снаряда, выпущенного из пушки, не учитывать сопротивление воздуха или влияние ветра, то будет допущена методическая ошибка. Если при измерении диаметра сферического тела пользоваться линейкой, то будет допущена методическая ошибка. Измерение в данном случае необходимо проводить штангенциркулем или другим прибором, позволяющим правильно охватить диаметр сферы. Для избавления от таких погрешностей необходимо усовершенствовать методику измерения. Необходимо учесть влияние на процесс измерения факторов, которые вносят значительные погрешности, путем ввода поправок в расчетные формулы.

К методическим погрешностям можно отнести вычислительные погрешности, связанные с округлением чисел при подстановке их в формулы и при последовательных вычислениях. К примеру, если при вычислении физической величины по формуле, в которую входит некоторое иррациональное число (, e или др.), подставим ее округленное значение, то результат вычисления получим с ошибкой. Если расчет физической величины совершается по основной формуле, в которую входят величины, найденные по другим формулам, то при округлении последних величин и подстановке их в основную формулу результат измерения получим с ошибкой. Для того чтобы учесть такие ошибки, результат промежуточного расчета округляют, по крайней мере, на один порядок точнее, чем точность исходных данных (см. п. 1.4). В качестве абсолютной погрешности иррациональных величин, входящих в формулу, у которых погрешность неизвестна, принимается половина известного младшего разряда.

Пример. Число  имеет значение =3,141592654…. Если в формулу подставляется =3,14, то допускается погрешность =0,005, равная половине одной сотой. Так же и с постоянными, погрешности которых неизвестны.

Приборные погрешности – ошибки, вызванные несовершенством изготовления измерительных приборов. Любой измерительный прибор невозможно изготовить абсолютно точно. Рассмотрим рычажные весы (рисунок 1.3). Если правый рычаг весов больше, чем левый, то в результате измерения значение массы будет получаться всегда меньше, чем в действительности. Такие погрешности присущи всем приборам. Кроме того, все приборы имеют цену деления, ограничивающую точность измерения.

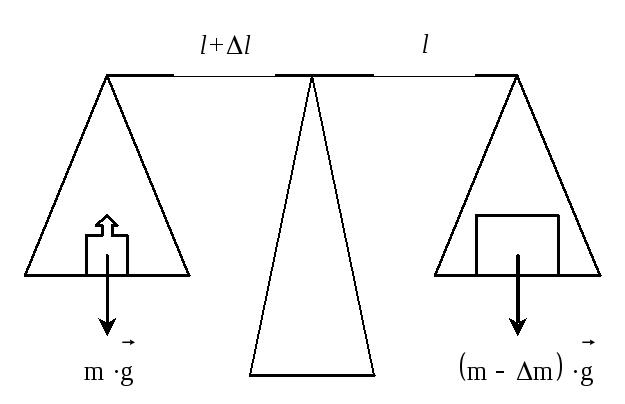
Рисунок 1.3 – Приборная погрешность рычажных весов

Для характеристики измерительных приборов используется понятие приведенной погрешности E (класса точности). Класс точности – отношение абсолютной погрешности X к предельному значению (диапазону) X_д измеряемой величины (т.е. к наибольшему значению, которое может быть измерено по шкале прибора). Приведенная погрешность является, по существу, относительной погрешностью, выраженной в процентах от диапазона:

E =X/X_д100 %. (1.6)

По приведенной погрешности приборы подразделяются на семь классов:

0,1; 0,2; 0,5 – лабораторные приборы;

1,0; 1,5; 2,5; 4 – технические приборы.

Завод, выпускающий прибор, гарантирует относительную погрешность измерения данным прибором, равную классу точности.

Зная класс точности прибора, можно определить абсолютную приборную погрешность

X_пр= EX_д/100. (1.7)

Класс точности указывается на шкале прибора числом, либо в техническом паспорте к прибору. Часто на шкале прибора вместо класса точности указывается абсолютная погрешность с указанием единицы измерения. Если ни на шкале прибора, ни в техническом паспорте нет данных о погрешности, то за абсолютную приборную погрешность принимают половину цены деления – половину значения физической величины, приходящейся на расстояние между двумя соседними делениями прибора. Для цифровых приборов и приборов, у которых стрелка скачет от деления к делению, в качестве приборной погрешности принимается цена деления.

3. Случайные погрешности – погрешности, которые изменяются случайным образом от опыта к опыту при повторных измерениях одной и той же величины. Эти погрешности являются следствием случайных, неконтролируемых помех, влияние которых на процесс измерения невозможно учесть непосредственно.

В качестве примера возникновения таких погрешностей можно привести разброс данных при измерении диаметра проволоки штангенциркулем. При изготовлении проволоки невозможно добиться того, чтобы ее диаметр по всей длине был один и тот же. Значения диаметра при повторных измерениях в различных сечениях проволоки будут иметь случайный характер и группироваться около некоторого среднего значения.

Оценку случайных погрешностей проводят методами теории вероятности и математической статистики. Дисциплина, изучающая случайные погрешности, называется теорией погрешностей. Согласно этой теории, случайные погрешности измерений подчиняются закону нормального распределения (закону Гаусса).

Смысл этого закона заключается в следующем. Допустим, мы хотим измерить некоторую физическую величину, истинное значение которой – X_ист. Используя какой-нибудь прибор, мы n раз пытаемся определить эту величину, но из-за случайных погрешностей, возникающих в процессе измерения, вместо X_ист получаем набор значений X₁, X₂,…, X_i,…, X_n-1, X_n. С помощью закона распределения нельзя указать точно, чему равно X_ист, но можно оценить вероятность P того, что X_ист окажется в интервале значений X_ср – X  X_ист X_ср + X или [X_ср – X, X_ср + X] (см. рисунок 1.2). Этот интервал называется доверительным интервалом, а вероятность P – доверительной вероятностью. По закону Гаусса эта вероятность определяется функцией плотности распределения

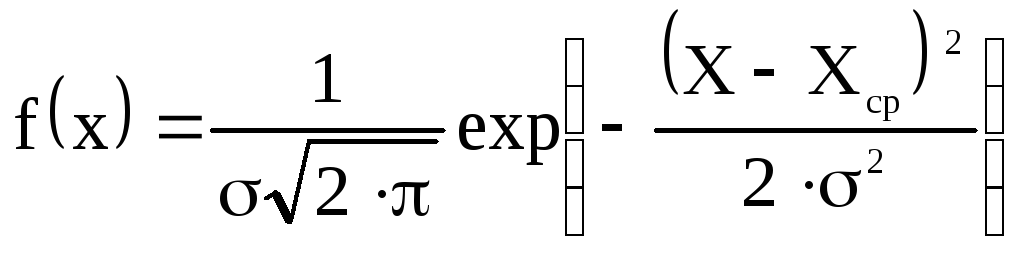(1.8)

и равна 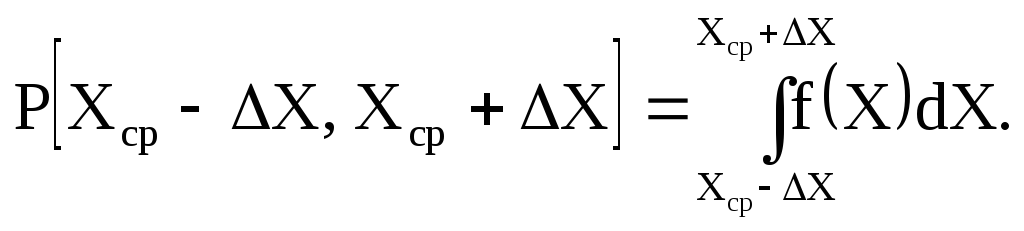(1.9)

Здесь X – набор значений, которые мы получаем в результате измерений, X_ср – определяется по формуле (1.3),  – среднеквадратичное отклонение

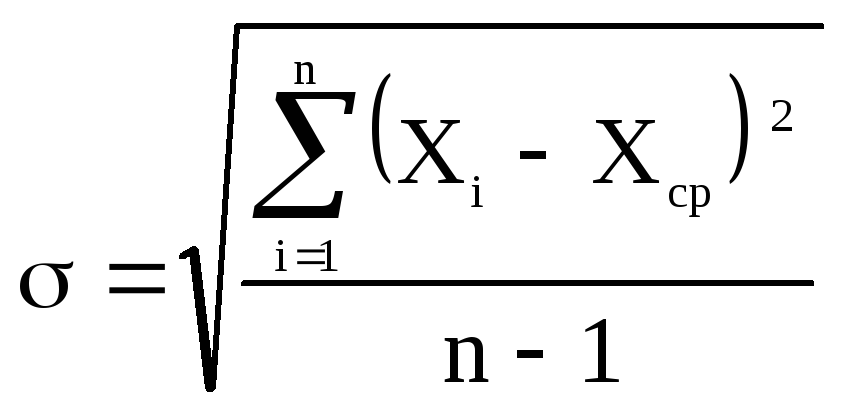, (1.10)

где X_i – i-е измерение, n – количество измерений.

Как видно из рисунка 1.4, гауссова кривая, имеющая на графике симметричный колоколообразный вид, характеризуется двумя параметрами: положением вершины X_ср и шириной 2 – расстояние между точками перегиба. Значение X_ср обычно и принимается за ту величину, которую надо было измерить, а  характеризует степень влияния случайных погрешностей на результаты измерения: чем меньше , тем уже гауссова кривая и, следовательно, тем точнее проведено измерение.

Обработка результатов измерений сводится к возможно более точному нахождению параметров гауссовой кривой X_ср и . Площадь под кривой Гаусса (рисунок 1.4) характеризует вероятность того, что при бесконечно большом количестве измерений (при одинаковых условиях) одной и той же физической величины ее истинное значение находится в доверительном интервале (1.5). Если в качестве доверительного взять интервал [X_ср – , X_ср + ], то вероятность нахождения истинного значения в этом интервале равна P = 0,683. При больших интервалах будет больше площадь под кривой и больше величина P.

При экспериментальных исследованиях невозможно произвести бесконечно большое количество измерений, поэтому возникает вопрос: как изменяется доверительный интервал в зависимости от числа измерений?

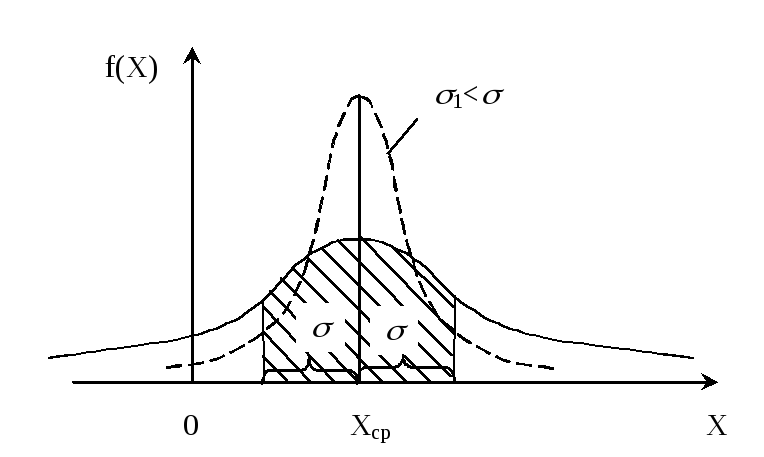
Рисунок 1.4 – Функция распределения Гаусса

В этом случае в качестве оценки среднеквадратичного отклонения принимается величина, называемая среднеквадратичной погрешностью

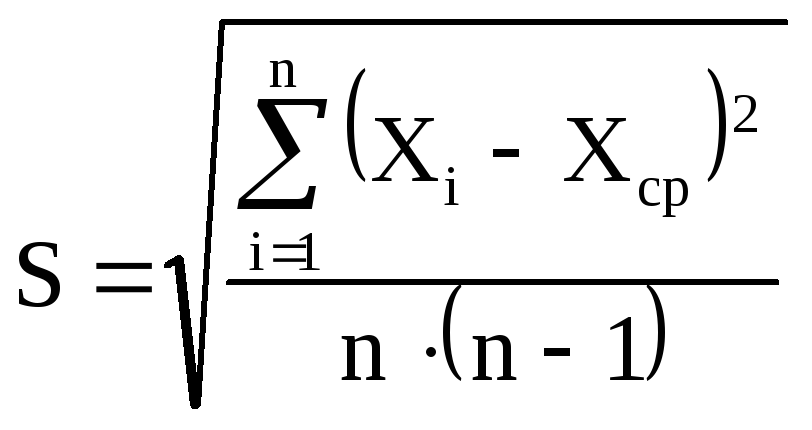. (1.11)

Существуют специальные таблицы коэффициентов Стьюдента, по которым можно определить, во сколько раз надо увеличить стандартный доверительный интервал [S], чтобы при определенном числе измерений n получить требуемую доверительную вероятность P.

Для нахождения случайной погрешности используется выражение

X_случ=t_P,nS, (1.12)

где t_P,n – коэффициент Стьюдента. Этот коэффициент зависит от доверительной вероятности P и от количества измерений n и находится по таблице 1.1.

Как правило, погрешность, допускаемая студентом в лабораторном практикуме, не должна превышать 5%. Поэтому, при проведении лабораторных работ, студент должен задаться доверительной вероятностью P=0,95 и в зависимости от количества измерений выбрать коэффициент Стьюдента.

Таблица 1.1 – Таблица коэффициентов Стьюдента

Кол-во опытов n	Доверительная вероятность P
	0,1	0,3	0,5	0,7	0,8	0,9	0,95	0,98	0,99	0,999
2	0,16	0,51	1,0	2,0	3,1	6,3	12,7	31,8	63,7	636
3	0,14	0,45	0,82	1,3	1,9	2,9	4,3	7,0	9,9	51,6
4	0,14	0,42	0,77	1,3	1,6	2,4	3,2	4,5	5,8	12,9
5	0,13	0,41	0,74	1,2	1,5	2,1	2,8	3,7	4,6	8,6
6	0,13	0,41	0,73	1,2	1,5	2,0	2,6	3,4	4,0	6,9
7	0,13	0,40	0,72	1,1	1,4	1,9	2,4	3,1	3,7	6,0
8	0,13	0,40	0,71	1,1	1,4	1,9	2,4	3,0	3,5	5,4
9	0,13	0,40	0,71	1,1	1,4	1,9	2,3	2,9	3,4	5,0
10	0,13	0,40	0,70	1,1	1,4	1,8	2,3	2,8	3,3	4,8

Может показаться, что с увеличением количества измерений коэффициент Стьюдента уменьшается (таблица 1.1), а следовательно, погрешность опыта можно сколь угодно уменьшить. Но это не так. С увеличением количества измерений в опыте коэффициент Стьюдента меняется очень мало, особенно при больших значениях n. Полностью избавиться от случайных погрешностей невозможно. Надо четко понимать, что увеличением числа измерений можно уменьшить только случайную составляющую погрешности. В то же время систематическая погрешность не уменьшается при увеличении n. Поэтому, если систематическая погрешность преобладает, увеличение числа измерений мало что дает. Если случайная погрешность превышает систематическую, то имеет смысл увеличить количество измерений и предпринять меры по снижению влияния случайных факторов на процесс измерения (если это возможно).