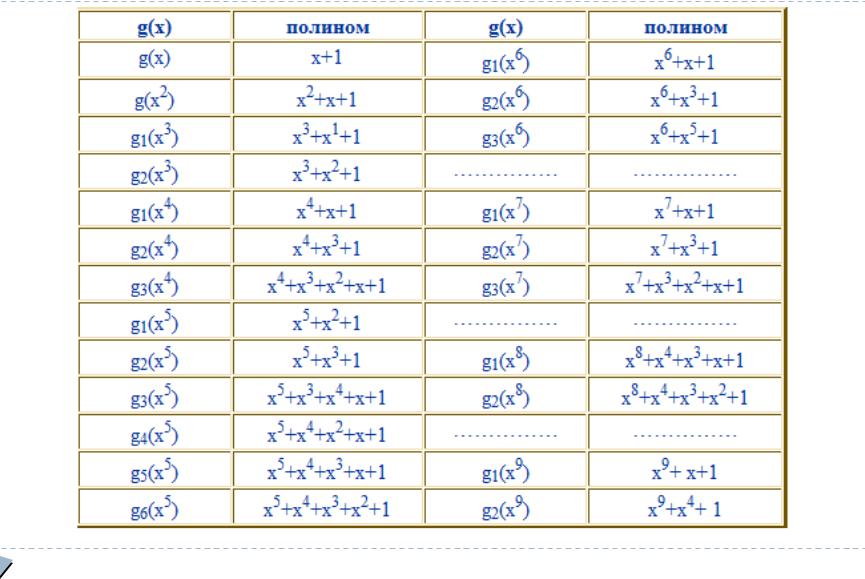
Еще таблица

Выбор образующего многочлена циклического кода по требуемой корректирующей способности

Выбор образующего многочлена для

исправления одиночных ошибок

Для исправления одиночных ошибок в n разрядной К.К. необходимо определить, какой разряд был искажен. Поэтому каждому вектору ошибки необходимо сопоставить свой остаток.

Для исправления одиночной ошибки должно быть выполнено условие:

2n – k – 1 = 2m – 1 ≥ Cn1 = n,

то есть 2m ≥ n

Из последнего равенства определяется число проверочных разрядов – это целое число с округлением log2(n + 1) в большую сторону.

В теории кодирования доказано, что если m и n связаны условием n = 2m – 1, то многочлен может быть представлен произведением

всех без исключения неприводимых многочленов степени которых являются делителями числа «m» от единицы до «m».

Причем всегда имеется хотя бы один многочлен степени «m».

Для исправления одиночных ошибок минимальная дистанция между двумя Р.К.К. должна быть:

d ≥ 2S + 1 = 2·1 + 1 = 3.

Таким образом, нам потребуется выбрать g(x), удовлетворяющий двум условиям:

и d = 3, где m – максимальная степень образующего многочлена,

а d – количество значащих

членов в нем.

Например:

Пусть n = 15; S = 1; тогда 2n – k – 1 ≥ n, откуда k = 11 и m = n – k = 15 – 11 = 4 или

Делителями числа «m» являются: 1; 2; 4. Разложим на сомножители:

Нас интересуют

неприводимые многочлены степени m = 4. Таких многочленов в разложении – три.

Проверим, дают ли они n = 15 различных остатков, чтобы поставить им в соответствие ошибки в различных разрядах.

Пусть g(x) = х4 + х3 + 1

Остатки будем получать путем деления X j на g(x).

Векторы ошибок младших разрядов имеют вид:

Степени соответствующих им многочленов меньше степени образующего многочлена g(x). Поэтому они сами являются

остатками при нулевой целой части.

Остаток, соответствующий вектору ошибки в следующем старшем разряде, получаем при делении 00...10000 на 11001, т.е.

Получили 15 различных остатков, а шестнадцатый остаток такой же, как первый.

Однако использовать для тех же целей многочлен

x4 + х3 + х2 + x + 1 нельзя.

При проверке числа различных остатков обнаруживается, что их у него не 15, а только 5

Это объясняется тем, что многочлен x4 + х3 + х2 + x + 1 входит в разложение не только двучлена x15 + 1, но и двучлена х5 + 1.