6.Исследование функций

6.1Краткие сведения из теории Возрастание и убывание функции. Точки экстремума

Функция f(x) называется возрастающей (неубывающей) на

некотором интервале (a,b), если			для	любых двух чисел x1	и x2 (a,b)
таких, что x1< x2	выполняется		f (x1 )< f( x2) (f (x1 )≤ f( x2)).
Функция	f(x)	называется		убывающей (невозрастающей) в
некотором интервале (a,b), если для любых двух чисел x1 и x2					(a,b) таких,
что x1< x2 выполняется неравенство f (x2)< f( x1) (f (x2)≤ f( x1)).

Правило.

Если функция f (x) дифференцируема на интервале (a,b) и f /(x )>0 (f /(x )<0), для любого x из этого интервала, то функция f (x )– возрастает (убывает) на этом интервале.

Функции возрастающие и убывающие, а также функции невозрастающие и неубывающие называются монотонными.

Говорят, что функция f(x) в точке x0 имеет максимум, если при любом достаточно малом h>0 выполняются условия f(x0 – h)< f(x0) и f(x0+ h)<

f(x0). В точке x0 имеется минимум , если f(x0-h)>f(x0) и f(x0+h)>f(x0).

Точка x0 (максимума или минимума) называется точкой экстремума функции.

Точки, в которых f /(x)=0 или f /(x) не существует (f /(x)=∞), называются

критическими точками первого рода.

Точки экстремума следует искать среди этих критических точек.

Необходимое условие экстремума.

Если x0 – точка экстремума функции y= f(x), то производная функции в этой точке либо равна нулю, либо бесконечности (f /( x0)=0, f /( x0)=∞).

Достаточное условие экстремума.
Критическая точка x0 является точкой экстремума функции y= f(x), если
при переходе через точку x0 (слева направо)						f /(x)	меняет знак. При этом,
если знак меняется с			«+»	на «–», то точка x0			есть точка максимума
функции, а если		f /(x) меняет знак с			«–» на	«+»,	то эта точка есть точка
минимума функции.								f /(x) не
Если же при переходе через критическую точку слева направо
меняет знак, то функция			f(x)	в этой точке экстремума не имеет.
Второе достаточное условие. Если в точке x= x0 первая производная
функции	f(x) равна нулю:			f /(x0)=0,	то при	x= x0	имеет место максимум,
если f	//(x0)<0,	и минимум, если			f //(x0)>0.	Если же f //(x0)=0,		то для

заключения об экстремуме в этой точке требуется дальнейшее исследование

75

(предполагается, что функция f(x) в окрестности точки x=x0 имеет непрерывную вторую производную).

Выпуклость, вогнутость функции. Точки перегиба

Говорят, что на интервале (a,b) кривая вогнутая, если она лежит выше касательной, проведенной в любой ее точке.

Говорят, что на интервале (a,b) кривая выпуклая, если она лежит ниже касательной, проведенной в любой ее точке.

Если f //(x )<0 в интервале (a,b), то график функции является выпуклым в этом интервале; если же f //(x )>0, то в интервале (a,b) график функции– вогнутый.

Точка кривой, отделяющая ее выпуклость от вогнутости и наоборот,

называется точкой перегиба.

Точки кривой, в которых f //(x)=0 или не существует ( f //(x)=∞), называются критическими точками второго рода.

Точки перегиба следует искать среди критических точек второго рода. Если при переходе через критическую точку второго рода x0 слева направо и наоборот f //(x) меняет знак, то точка x0 является точкой перегиба

функции y= f(x).

Асимптоты

Прямая L называется асимптотой непрерывной кривой y= f(x), если расстояние от прямой L до точки M(x,y), принадлежащей кривой, стремится к

нулю по мере удаления точки по этой кривой в бесконечность.
Различают	асимптоты:	1)	вертикальные,	2)	наклонные,
3) горизонтальные.
Прямая x=a называется вертикальной асимптотой кривой						y= f(x),

если при x→a (справа или слева) значение функции стремится в бесконечность, то есть выполнено одно из следующих условий:

lim	f (x) = ±∞ , lim	f (x) = ±∞
x→a+0	x→a−0
Прямая y=kx+b является наклонной асимптотой кривой										y= f(x),
если существуют пределы		f (x)
	k = lim		,	b = lim	[	f (x) − kx		]
	x→±∞	x		x→±∞
Прямая y= b является горизонтальной асимптотой кривой										y= f(x),
если существуют пределы b = lim				f (x) , и	k = lim		f (x)		= 0 (горизонтальная
								x
		x→±∞				x→±∞

асимптота является частным случаем наклонной асимптоты при k=0 ).

76

План исследования функции:

Найти область определения функции, поведение функции в окрестностях точек разрыва и при x→±∞.

Установить четность, нечетность, периодичность функции. Найти точки пересечения графика с осями координат. Найти асимптоты.

Найти интервалы возрастания и убывания функции, точки экстремума функции.

Найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

Используя полученные результаты исследования, построить график функции.

План исследования функции реализуем для функции

y = 3 2x2 − x3

Область определения функции: (–∞;+∞).

Для исследуемой функции, f(–x) ≠ f(x) и f(–x)≠ – f(x), следовательно, данная функция не является ни четной, ни нечетной. Функция не периодична.

Найдем точки пересечения функции с осью Ox, для чего y=0. Тогда

3 2x2 − x3 =0 , 2x2 − x3 =0 , x = 0, x = 2. Значит, график функции проходит через точки (0;0) и (2,0). Найдем точки пересечения графика с осью Oy, для чего x = 0, тогда y=0. Значит, график функции проходит через точку с координатами (0;0)

Асимптоты Вертикальных асимптот нет, так как функция определена всюду. Наклонные асимптоты.

y=kx+b

f (x)

3

2x2 − x3

x 3

2

−1

2

k = lim

x

−1

= −1,

= lim

= lim

= lim

3

x

x

x

x

x→±∞

x→±∞

x→±∞

x→±∞

77

b = lim

[f (x) − kx]= lim

(

3

2x

2 − x3

+ x

)

=

x→±∞

x→±∞

)

(

)

(

2

3 2x2

− x3

3 2x2 − x3 + x

− x3 2x2 − x3 + x2

= lim

=

2

x→±∞

(3 2x2 − x3 ) − x3 2x2 − x3 + x2

= lim

2x2

− x3 + x3

= lim

2x2

=

(3 2x2 − x3 )2

x→±∞ (3 2x2 − x3 )2

− x3 2x2 − x3 + x2

x→±∞

− x3 2x2 − x3 + x2

= lim

2x2

= lim

2x

2

=

2

2

x→±∞

x→±∞

2

2

1 + x2

3

2

1

2

x2

3

−1

− x2

3

−

x

2

−

− 3

−1 +1

x

x

x

x

= lim

2

=

2

=

2

2

2

2

1

+1 +

1

3

x→±∞

3

−1 − 3

−1

+1

x

x

Уравнение наклонной асимптоты y = −x + 2

3

y/ =(3 2x2 − x3 )/ =

4x − 3x2

=

x(4 − 3x)

=

4 − 3x

(2x2 − x3 )

2

3x3 x(2 − x)

2

33 x(2 − x)

2

33

y/ = 0 когда 4–3x =0, а y/ = ∞ когда 3

x(2 − x)2

=0

/

4

/

y = 0 в точке

x =

3 , а y = ∞ в точках x=0, x=2

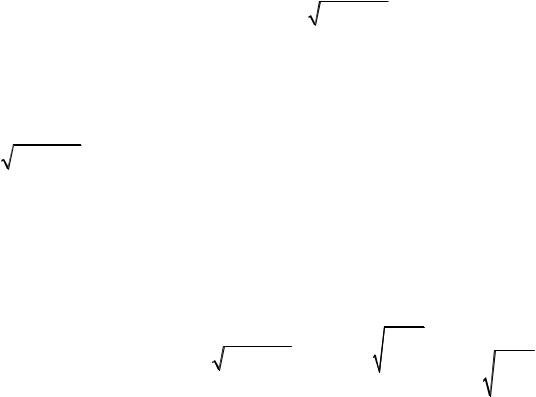
Отметим эти критические точки

y/

на числовой

оси

и

определим

знак

–

+

–

–

производной

в каждом полученном

интервале.

0

4

2

y

На

4

интервале

3

x (−∞;0)

3

;+∞

производная отрицательная, следовательно, функция на этом интервале

убывает, а на интервале

0;

4

производная положительная,

то функция

x

3

возрастает. Точки входят в область определения. При переходе через критическую точку x=0 производная меняет знак с "–" на "+",

78

следовательно, x=0– точка минимума, ymin = f(0)= 0 –минимальное значение функции.

При переходе через критическую точку x = 43 производная меняет знак

с "+" на "–", следовательно,	x =	4	– точка максимума,	ymax =		4		=	2	3	4 –
		3			f	3			3

максимальное значение функции.

При переходе через критическую точку x=2 производная не меняет знак, следовательно, эта точка не является точкой экстремума.

	//										4 − 3x			/				1						4 −	3x				/
y			=												=																		=
							33 x(2 − x)2										3				3 x(2 − x)2
=	1				(4 − 3x)/ 3 x(2 − x)2 − (4 − 3x)(3 x(2 − x)2 )/																																	=
	3													3		x(2 − x)2
											2														1													2
							− 33				x(2 − x)			− (4 − 3x)																						((2 − x)						− 2x(2 − x))
=	1																							3(3 x(2 − x)2 )2
	3																						(3 x(2 − x)2							)2
											2													4 − 4x + x2 − 4x													+ 2x2
							− 33				x(2 − x)			− (4 − 3x)
=	1																								3(3 x(2 − x)2												)2						=
	3															(3 x(2 − x)2 )2
=		1					− 9x(2 − x)2 − (4 − 3x)(4 − 8x + 3x2 )																										=
		3									3(3 x(2 − x)2					)2	(3 x(2 − x)2 )2
=	1						− 9x(4 − 4x + x2 )− (16 − 32 x +12x2 −12x + 24 x2 − 9x3 )																																									=
																					(3 x(2 − x)2							)4
	9
	1						− 36 x + 36 x2							− 9x3 −16 + 44 x −														36 x2 + 9x3											1					−16			+ 8x
=														(3										4														=						4
	9																																						9
																x(2 − x)2 )																												x 3 (2 − x)3
											2 − x																																					8
= −					8								= −			8								1			= −									8
																					4												4
			9					4			(2 − x)3					9							(2 − x)3													(2 − x)3
									x 3											x 3											9x 3
											8														5													5

=

=

	4	Ни		в одной точке y// не обращается в нуль, а y// = ∞ когда
		5
x 3 (2 − x)				=0 x1 =0, x2 =2.
			3

79

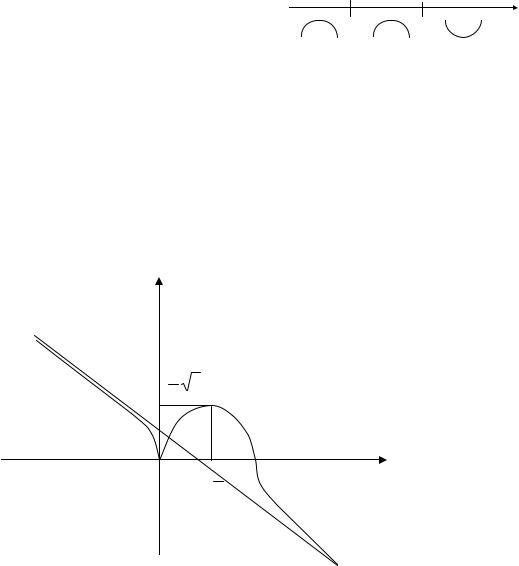
Отметим эти критические точки				–		–		+	y//
на числовой оси и определим знак									.
второй	производной	в	каждом		0		2		y
полученном интервале.		x (–∞;2) вторая
На	интервале			производная				отрицательная,
следовательно, функция		на	этом интервале		выпуклая,		а	на	интервале

x (2;+∞) вторая производная положительная, значит функция вогнутая. Точки входят в область определения. При переходе через критическую точку x1 =0 вторая производная знак не меняет, следовательно, точка x1 =0 не является точкой перегиба. При переходе через критическую точку x2=2 вторая производная меняет знак с "–" на "+", следовательно, x2=2– точка перегиба, y = f(2)= 0– значение функции в точке перегиба.

Построим график функции y

y = –x+2/3

2 3 4

3

0	4	2	x
	3

			6.2 Решение типовых задач и примеров
Пример		1. Исследовать методами дифференциального исчисления
функцию y =		x3	и построить ее график.
		− x2
4

Решение. 1. Область определения функции: (–∞;–2) (–2;2) (2;+∞).

Вычислим lim f (x) :

x→m∞

80

lim

x3

= lim

x3

= lim

x

= −∞

4

4

x→+∞ 4 − x2

x→+∞

2

x→+∞

x

−1

−1

x2

x2

lim

x3

= lim

x3

= lim

x

= +∞

− x2

4

4

x→−∞ 4

x→−∞

2

x→−∞

x

−

1

−1

x2

x2

2. Исследуем функцию на четность, нечетность и периодичность:

f (−x) =

(−x3 )

=

−x3

= −

x3

= − f (x) – функция нечетная, и ее

4 − (−x2 )

4 − x2

4 − x2

график симметричен относительно начала координат. Функция не периодическая.

3. Найдем точки пересечения функции с осью Ox: y=0,

x3

3

=0 x

4 − x2

= 0 x =0, значит, график функции проходит через точку (0;0).

Найдем точки пересечения функции с осью Oy: x = 0. Получаем y=0.

Таким образом, точка с координатами (0;0)– единственная точка

пересечения графика с осями координат.

4. Данная функция не определена при x = –2 и при x = 2.

lim

x3

=

(− 2 + 0)3

=

−8

=

−8

=

−8

=

−8

= −∞

4 − x2

4 − (− 2 + 0)2

− (4 − 4 0 + 02 )

4 − (4 − 0)

4 − 4 + 0

0

x→−2+0

4

lim

x3

=

(− 2 − 0)3

=

−8

=

−8

=

−8

=

−8

= +∞

4 − x2

4 − (− 2 − 0)2

− (4 + 4 0 + 02 )

4 − (4 + 0)

4 − 4 − 0

− 0

x→−2−0

4

lim

x3

=

(2 + 0)3

=

8

=

8

=

8

=

8

= −∞

4 − x2

− (2 + 0)2

4 − (4 + 4 0 + 02 )

4

− (4 + 0)

4

− 4 − 0

x→2+0

4

− 0

lim

x3

=

(2 − 0)3

=

8

=

8

=

8

=

8

= +∞

4 − x2

− (2 − 0)2

4 − (4 − 4 0 + 02 )

4

− (4 − 0)

4

− 4 + 0

0

x→2−0

4

Следовательно, x = 2 и x =-2-уравнения вертикальных асимптот.

Наклонная асимптота y = kx + b , где

	k = lim	f (x)	;	b = lim	( f (x) − kx).
		x
	x→m∞			x→m∞

Найдем k и b:

81

k = lim

x3

= lim

x3

= lim

1

= −1

,

− x2 )

4

x→m∞ x(4

x→m∞

3

x→m∞ 4

x

−

1

−1

x2

x2

x3

x3

x3 + 4x − x3

4x

b = lim

− (− x)

= lim

+ x

= lim

= lim

=0 .

4 − x2

4

− x2

4 − x2

− x2

x→m∞

x→m∞

x

→m∞

x→m∞ 4

Итак, y= – x - уравнение наклонной асимптоты.

5.

y/ =

3x

2 (4 − x2 )− x3 (−2x)

=

12x2 − 3x4 + 2x4

=

12x2

− x4

(4 − x2 )2

(4 − x2 )2

(4 − x2 )2

x

2

(12

− x

2

)= 0

x1 = 0, x2,3 = ±2

3

y

0,

0,

/ =

−

2 =

y/ =

x

= ±2

∞

4

x

0

∞,

4,5

,

Отметим эти критические точки

y/

на

числовой

оси и определим знак

+

+

+

+

производной

в

каждом

полученном –

–

интервале.

−2 3

-2

0

2

2 3

y

На интервалах

x (−∞;−2

3 ) (2

3;+∞)

производная

отрицательная,

следовательно,

функция

на

этих

интервалах убывает, а

на

интервалах

x (−2 3;2

3 ) производная положительная, то функция возрастает.

При переходе через критическую точку x2 = −2

3 производная меняет

знак

с

"–"

на "+",

следовательно,

x2 = −2

3 –точка

минимума,

ymin = f (− 2

3)= 3 3 –минимальное значение функции.

При переходе через критическую точку x4 = –2

производная не меняет

знак, следовательно, точка x4 = –2 не является точкой экстремума.

При переходе через критическую точку x1 = 0

производная не меняет

знак, следовательно, точка x1 =0 не является точкой экстремума.

При переходе через критическую точку x5 = 2

производная не меняет

знак, следовательно, точка x5 = 2 не является точкой экстремума.

При переходе через критическую точку

x3 = 2

3

производная меняет

знак

с

"+"

на

"–",

следовательно,

x3 = 2

3 –точка

максимума,

ymax = f (2 3)= 3

3 –максимальное значение функции.

82

6.

/

(24x − 4x

3

) (4 − x

2

)

2

−(12x

2

− x

4

) 2

(4 − x

2

) (−2x)

y

//

12x2 − x4

=

=

=

4

− x2 )

2

(4 − x2 )

(4

= (4 − x2 ) ((24x − 4x3 ) (4 − x2 )+ 4x(12x2 − x4 ))=

(4 − x2 )4

=

(24x −

4x3 ) (

4 − x2 )+ 4x(12x2 − x4 )

=

(4 − x2 )3

=

96 x − 24x3 −16 x3 + 4x5 + 48x3 − 4x5

=

96 x + 8x3

(4 − x2 )3

(4 − x2 )3

8x(12 + x

2

)= 0

0,

x1 = 0

y//

0,

y// =

=

2

= ±2

4 − x

= 0

∞, x

2,3

∞,

y//= 0 при x = 0, y// =∞ при x = –2 и при x = 2.

Отметим критические

точки на

//

числовой оси и определим знак второй

+

–

+

–

y

y

производной

в

каждом

полученном

–2

0

2

интервале.

x (–∞;–2) (0;2)

вторая производная положительная,

На интервалах

следовательно,

функция

на

этих интервалах

вогнутая,

а на

интервале

x (–2;0) (2;+∞) вторая производная отрицательная, то функция выпуклая. Точки x = –2 и x = 2 не входят в область определения.

При переходе через критическую точку x1=0 вторая производная меняет знак с "–" на "+", следовательно, x1=0– точка перегиба, y = f(0)= 0– значение функции в точке перегиба.

7. Используя полученные результаты, построим график

83

x= –2

y

3 3

x=2

−2 3		2 3
–2	2	x

−3 3

y =–x

Пример 2. Исследовать методами дифференциального исчисления функцию y =3 − ln x x+1 и построить ее график.

Решение.

1. Область определения функции: (–∞;–1) (0;+∞).

Вычислим

lim

f (x) :

x→m∞

x

x

x

lim 3

− ln

= lim 3 −

lim ln

=3 − ln lim

=3 − ln1 =3

x +1

x→+∞

x +1

x→+∞

x→+∞

x→+∞ x +1

x

x

x

lim 3

− ln

= lim 3 −

lim ln

=3 − ln lim

=3 − ln1 =3

x +1

x→−∞

x +1

x→−∞

x→−∞

x→−∞ x +1

2. Исследуем функцию на четность, нечетность и периодичность:

	− x				x
y(− x)=3 − ln			=3	− ln
					x −1
	− x +1

– функция является ни четной и ни нечетной (функция общего вида). Функция не периодическая.

3. Найдем точки пересечения функции с осью Ox: y=0, 3 − ln x x+1 = 0

ln	x		=3	x		= e3 x(1 − e3 )= e3	x =		e3	≈ −1,05. График функции
	x +1			x +1					−e3
							1

проходит через точку (–1,05;0).

84

Найдем точки пересечения функции с осью Oy: x = 0. Точка x = 0 не входит в область определения.

Таким образом, точка с координатами (–1,05;0) – единственная точка пересечения графика с осями координат.

Данная функция не определена при x = 0 и при x = –1. Рассмотрим

		− ln	x		=3 − ln	+ 0	=3	− ln 0	=3 − (− ∞)= +∞, а для	x→ –0
lim	3
						+ 0 +1
x→+0			x +1

поведение функции рассматривать не будим так как интервал (–1;0) не входит в область определения.

Рассмотрим

− ln

x

=3 − ln

−1 − 0

=3 − ln

−1

=3

− ln ∞ = −∞, а для x→ –

lim

3

−1

− 0

+1

− 0

x→−1−0

x +1

1–0 поведение функции рассматривать не будим так как не входит в область определения интервал (–1;0).

Следовательно, x = 0 и x =-1-уравнения вертикальных асимптот.

Наклонная асимптота y = kx + b , где

k = lim

f (x)

;

b = lim

( f (x) − kx).

x

x→m∞

x→m∞

Найдем k и b:

x +1

x +1− x

3 −ln

x

ln

x

= − lim

= − lim

x

(x +1)2

1

k = lim

x +1

x +1

= − lim

= 0 ,

1

x→m∞

x

x→m∞

x

x→m∞

x→m∞ x(x +1)

b =

x

x

x

lim

3

− ln

=3 − lim ln

=3 − ln lim

=3 − ln1

=3 − 0 =3

x +1

+1

.

x→m∞

x +1

x→m

∞

x→m∞ x

Итак, y= 3 - уравнение наклонной асимптоты.

5. y

/

x

/

x +

1

x +1 − x

1

=

3 − ln

= −

= −

x

x

(x +1)2

x(x +1)

+1

y / =

0,

-1 ≠ 0

y /

=

0,

всегдаотлично отнуля

x(x +1)= 0

x

= 0,x

= −1

∞,

∞,

2

1

Отметим эти критические точки на числовой оси и определим знак производной в каждом полученном интервале.

На интервалах

–			–	у/
				у
–1		0

85

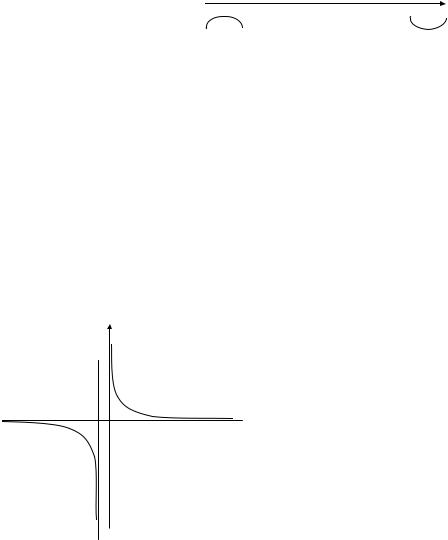
x (− ∞;−1) (0;+∞) производная отрицательная, следовательно, функция на этих интервалах убывает. Точек экстремума нет, так как в области определения функции производная знак не меняет, а точки х= –1 и х=0 и интервал (–1;0) не входят в область определения.

6.

y

//

1 /

1 /

=

2x +1

=

−

=

−

x2

x2 (x +1)2

x(x +1)

+ x

0,

2x +1 = 0

x

= −

1

y// =

y// =

0,

2

x2 (x +1)2 = 0

1

∞,

x2 = −1, x3 = 0

∞,

Отметим критические

точки на

–

+

числовой оси и определим знак второй

–1

−

1

производной

в каждом полученном

0

интервале.

2

x (–∞;–1) вторая

производная

отрицательная,

На интервалах

следовательно,

функция

на

этих интервалах выпуклая,

а на интервале

x (0;+∞) вторая производная положительная, то функция вогнутая.

Точки x = –1и x = 0 и интервал (–1;0) не входят в область определения.

7. Используя полученные результаты, построим график

у

3

х

–1,05 0

Задача 3. Требуется изготовить закрытый цилиндрический бак объемом V. Каким должны быть его размеры, чтобы на его изготовление ушло наименьшее количество материала?

86

Решение. В задаче, требуется определить какими должны быть радиус и высота цилиндра, чтобы при заданном объеме V его полная поверхность была минимальной.

Полная поверхность цилиндра: S = 2πRH+ 2πR2. (R>0)

Следует определить наименьшее значение этой функции. В данной функции неизвестные переменные R и H. Но в свою очередь V=πR2H.

Тогда H =

V

.

πR 2

Подставляя в формулу полной поверхности цилиндра, получаем

S = 2 πR

V

+ 2 πR 2

или

S =

2 V

+ 2 πR2

πR 2

R

Функция S – функция одной переменной R. Теперь найдем

минимальное значение функции S.

Для этого найдем производную первого порядка по R и приравняем к

нулю.

/

/

S

/

2 V

+ 2

πR

2

2 V

2

/

= −

2 V

+ 4 πR =

4 πR3 − 2 V

=

R

=

+ (2 πR

)

R 2

R 2

R

/

4 πR3 − 2 V

=

0

3

3

3

S

=0, когда

4πR

– 2V=0

4πR = 2V 2πR

=V

R 2

V

V

R 3 =

R = 3

2 π

2 π

Тогда, если R <

3

V

, то S/<0 , а если R > 3

V

, S/>0.

2 π

2 π

Следовательно, при R = 3

V

функция S достигает свое минимальное

2 π

значение.

Найдем высоту H.

2

1

H =

V

=

V

=

V

=

2

3

V

3

= 23

V

, то есть H=2R.

πR

2

V

2

2

1

2 π

V

3

π

3

π

3

2 π

π

2 2

2

3

π

3

Ответ: R =

3

V

, H=2R.

2 π

87

6.3 Задания на контрольную работу

Задание 1. Исследовать методами дифференциального исчисления функцию y= f(x) и, используя результаты исследования, построить ее график.

1.	а)	y =	x2 −3x −6
			x +1
	б) y = (x −1) e−x

3.а) y = 4x − x2 +1

x+ 2

б)

y = ln

x

−1

5.

x

− 2

а)

y =

2 − 4x2

1− 4x2

б) y = ln(x2 +1)

7.

а) y =

3x − 2x2

1− x

9.

б) y = (x +1) e2 x−1

а) y =

3x − 2x2 +1

x − 2

б)

y = ln

x −1

+ 3

x

2.	а)	y =		x2 − 4x
				x − 2
4.	б) y = ln(4 + x2 )
	а)	y =		x3
				x2 + 2x −3
	б) y = (2 + x2 ) e−x2

6.а) y = x2 −6x + 4

x2 − 4

б) y = xex2

8.а) y = x2 −3x −3

x−1

10.	б) y = ln(x2 +3)
	а)	y =	3x
			9 − x2
	б)	y = e2 x−x2

Задание 2. Решить задачу на экстремум.

Определить максимальную площадь равнобедренного треугольника, боковая сторона которого равна l.

Требуется вырыть яму конической формы с образующей l=3м. При какой глубине ямы ее объем будет наибольший?

Открытый бак имеет форму цилиндра. При объеме V=5м3. Каковы должны быть радиус основания и высота цилиндра, чтобы его поверхность была наименьшей?

Определить наибольшую площадь равнобедренного треугольника, вписанного в круг радиуса R.

Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R.

Чему должны быть равны радиус основания, высота и образующая прямого кругового конуса для того, чтобы при заданном объеме V он имел наименьшую полную поверхность?

Определить наименьшую площадь равнобедренного треугольника, описанного вокруг окружности радиуса r.

88

Найти радиус и высоту конуса наименьшего объема, который можно описать около шара радиуса R.

Резервуар открытый сверху, имеет форму прямоугольного параллелепипеда с квадратным основанием. Каковы должны быть размеры, чтобы на его изготовление ушло наименьшее количество материала, если он должен вмещать 300л. воды?

Чему должны быть равны радиус основания, высота и образующая прямого кругового конуса для того, чтобы при заданной боковой поверхности S он имел наибольший объем?

89

7. Функции нескольких переменных

7.1.Краткие сведения из теории

Предел и непрерывность функции нескольких переменных

Если каждой точке M D En ставится в соответствие по известному закону некоторое число u , то говорят, что на множестве D задана функция u=f(M), или u=f(x1,…,xn). При этом множество D называется обла-

стью определения функции.

Число a называется пределом функции u=f(M) в точке P (или при M→P), если для любого >0 можно указать такое число = ( )>0, что для всех точек M, удовлетворяющих условию 0< (M,P)< , выполняется неравенство |f(M)–a|< и записывают

lim f (M ) = a, или	lim	f (x1,K,xn ) = a.
M →P	x1→p1
	LLL
	xn →pn
Функция u=f(M) называется непрерывной в точке P, если предел
в этой точке существует и равен значению функции в этой точке, т.е.
lim f (M ) = f (P),	или	lim f (x1,K,xn ) = f ( p1,K, pn ) .
M →P		x1→p1
	LLL
		xn →pn
	Частные производные

Пусть функция u=f(x1,x2,…xn) определена в некоторой окрестности точки M, включая саму эту точку. Дадим аргументу xk приращение xk, тогда функция тоже получит приращение

k u = f (x1,..., xk + xk ,..., xn ) − f (x1,..., xk ,..., xn ) .

Частной производной от функции u=f(x1,x2,…xn) по независимой переменной xk называется предел (если он существует и конечен):

	lim		k u .
	xk →0		xk		∂u
Обозначают						или fx′k . Таким образом, по определению:
					∂xk
	∂u					k u .
		= fx′k =		lim
	∂xk			xk →0		xk

Отметим, что частная производная по независимой переменной xk вычисляется при условии, что все другие переменные постоянны. Для частных производных справедливы обычные правила и формулы дифференцирования.

Частными производными 2-го порядка функции u=f(x1,x2,…xn) называются частные производные от ее частных производных первого порядка. Производные 2-го порядка обозначаются следующим образом:

90

∂

∂u

∂

2

u

′′

∂

∂u

∂

2

u

=

=

,

=

=

′′

и т.д.

2

fxk xk

∂xk ∂xl

fxk xl

∂xk

∂xk

∂xk

∂xl

∂xk

Аналогично определяются производные порядка выше второго. Отметим, что результат многократного дифференцирования по различ-

ным переменным не зависит от очередности дифференцирования, если получающиеся при этом частные производные непрерывны. Если дифференцирование производится по различным переменным, по полученные частные производные называются смешанными.

Производные сложных функций

Пусть z = f (x; y) – функция двух переменных x и y, каждая из которых,

всвою очередь, является функцией независимой переменной t:

x= x(t), y = y(t). Тогда функция z = f (x(t); y(t)) является сложной функцией

независимой переменной t, а переменные x и y – промежуточными переменными. И пусть функции f (x; y), x(t), y(t) – дифференцируемы. Полная про-

изводная этой сложной функции находится по формуле:

dz	=	∂z	dx	+	∂z	dy .	(7.1)
dt		∂x	dt		∂y	dt

Для сложной функции, у которой число промежуточных переменных больше двух, производная находится аналогично. Например, если

u = f (x; y;z) , где x = x(t), y = y(t), z = z(t) , то формула полной производной

примет вид:

du	=	∂u	dx	+	∂u	dy	+	∂u	dz .	(7.2)
dt		∂x	dt		∂y	dt		∂z	dt

Рассмотрим более общий случай. Пусть z = f (x; y) – функция двух пе-

ременных x и y, каждая из которых, в свою очередь, является функцией двух независимых переменных u и v: x = x(u;v) , y = y(u,v). Тогда функция

z = f (x(u;v), y(u;v)) является сложной функцией двух независимых перемен-

ных u и v, а переменные x и y – промежуточные переменные. И пусть функции f (x; y), x(u;v), y(u;v) – дифференцируемы. Частные производные этой

сложной функции z = f (x(u;v); y(u;v)) находятся по формулам:

∂∂uz = ∂∂xz ∂∂ux + ∂∂yz ∂∂uy ;

(7.3)

∂∂vz = ∂∂xz ∂∂xv + ∂∂yz ∂∂yv.

Производные неявных функций

91

Производная неявной функции y = y(x), заданной с помощью уравнения F(x; y) = 0, где F(x; y) – дифференцируемая функция переменных x и y,

находится по формуле:				dy		∂F ∂x
∂F	+ ∂F dy = 0		или		= −		(7.4)
∂x	∂y dx			dx		∂F ∂y
при условии		∂F	≠ 0.
		∂y

Частные производные неявной функции двух переменных z = f (x; y) , заданной с помощью уравнения F(x; y;z) = 0 , где F(x; y;z) – дифференци-

руемая функция переменных x, y и z, находятся по формулам:

∂∂Fx + ∂∂Fy ∂∂yx + ∂∂Fz ∂∂xz = 0 и ∂∂Fy + ∂∂Fx ∂∂yx + ∂∂Fz ∂∂yz = 0.

Учитывая, что y не зависит от x, а x не зависит от y, т. е. ∂∂yx = 0, ∂∂yx = 0 ,

получаем
∂z = −	∂F ∂x	,		∂z = −		∂F ∂y	(7.5)
∂x	∂F ∂z			∂y		∂F ∂z
при условии			∂F		≠ 0.
			∂z
	Дифференциал функции нескольких переменных
Полным приращением u функции u = f (x1, x2 ,..., xn ) в точке
M (x1, x2 ,..., xn ), соответствующим приращениям аргументов								x1, x2 ,..., xn ,
называется:
u = f (x1 +			x1, x2 +			x2 ,..., xn +	xn ) − f (x1, x2 ,..., xn ) .	(7.6)

Полным дифференциалом 1-го порядка du функцииu = f (x1, x2 ,..., xn ) в

точке M (x1, x2 ,..., xn ) называется главная, линейная относительно приращений аргументов, часть полного приращения функции:

du = A1

x1 + A2

x2 +...+ An

xn .

Для полного дифференциала 1-го порядка функции u = f (x1, x2 ,..., xn )

справедлива следующая формула:

du =

∂u

dx

+

∂u

dx

+...+

∂u

dx

n

.

(7.7)

∂x

1

∂x

2

2

∂x

n

1

Дифференциалом 2-го порядка d2u

функцииu = f (x , x

2

,..., x

n

) называ-

1

ется дифференциал от ее дифференциала d 2u = d(du).

Аналогично определяются дифференциалы более высоких порядков. Дифференциал dmu = d(dm−1u) порядка m символически выражается формулой:

92

	m		∂		∂			∂		m
											u ,
d			∂x	dx1 + ∂x			dx2 +...+ ∂x
		u =				2			n	dxn
			1

которая раскрывается по биномиальному закону. Например, для функ-

	ции двух переменных z = f (x, y)					дифференциал 2-го порядка вычисляется по
	формуле:	∂2 z dx2		∂2 z			∂2 z dy2 .
	d 2 z =		+ 2		dxdy	+		(7.8)
				∂x∂y
		∂x2					∂y2

Экстремум функции нескольких переменных

Пусть функция u=f(M) определена в области D и точка M0 является внутренней точкой этой области. Говорят, что функция f(M) имеет в точке

M0 экстремум (максимум или минимум), если существует такая окрестность точки M0 , в которой для любой точки M из этой окрестности выполняется неравенство

f (M ) ≤ f (M0 ) или f (M ) ≥ f (M0 ) .

Если в точке в точке M0 функция f(M) имеет экстремум, то в этой точке ее частные производные либо равны нулю, либо не существуют.

		∂u		= 0.	(7.9)
		∂xi M0

Точки, в которых выполняются условия (7.9), называются стационарными точками функции u=f(M). Точки, в которых частные производные равны нулю или не существуют, называются критическими.

Рассмотрим функцию двух переменных u=f(x,y) в окрестности стационарной точки M0(x0, y0). Обозначим

A

=

∂2u

, A

=

∂2u

, A

=

∂2u

.

∂x2

∂x∂y

∂y2

11

12

22

=

A11

A12

= A A − A2 .

A12

A22

11

22

12

Достаточные условия существования точек экстремума для функции двух переменных:

1)Если >0, то точка M0 – точка экстремума, причем – максимум при A11<0, минимум при A11>0.

2)Если <0, то в точке M0 экстремум отсутствует.

3)Если =0, то требуется дополнительное исследование на на-

личие экстремума данной функции в точке M0.

Наибольшее и наименьшее значения функции

Если функция f (M ) дифференцируема в ограниченной замкнутой об-

ласти, то она достигает своего наибольшего (наименьшего) значения или в стационарной точке или в граничной точке области. Таким образом, для того,

93

чтобы найти наибольшее и наименьшее значения функции в замкнутой области, необходимо:

1)найти стационарные точки, расположенные в данной области, и вычислить значения функции в этих точках;

2)найти наибольшее и наименьшее значения на границе этой области;

3)из всех вычисленных значений выбрать наибольшее и наименьшее.

Производная по направлению. Градиент

Рассмотрим функцию z = f (M ) , определенную в некоторой окрестности точки M (x; y) , и произвольный единичный вектор

lr = (cosα;cosβ). Проведем в

направлении вектора l прямую MM1. Точка M1 имеет координаты

	(x +	x; y +	y) . Величина отрезка
				r L
	y+	y		l
			β	M1
	y		α
			M
		x	x+	x

MM1 равна l = ( x)2 +( y)2 . Функция f (M ) при этом получит приращение:

z = f (x + x; y + y) − f (x; y) .

Предел отношения	z	при
	l

l →0 (M → M1), если он существует и

конечен, называется производной функции z = f (M ) в точке M (x; y) по направлению

∂z = lim

∂l l→0

Рис. 7.1	∂z	, т.е.
вектора l и обозначается
	∂l

zl .

При нахождении производной по направлению пользуются фор-

мулой:
∂z	=	∂z cosα +	∂z cosβ .	(7.10)
∂l		∂x	∂y

Градиентом функции z = f (M ) в точке M (x; y) называется

вектор, координаты которого равны соответствующим частным произ-

водным	∂z	и	∂z , взятым в точке M (x; y) . Обозначается:
	∂x		∂y
graduuuuuurz =				∂z ;	∂z =	∂z ir +	∂z rj .		(7.11)
				∂x	∂y	∂x	∂y
Учитывая определение градиента, формулу 7.10 можно представить в
виде:							uuuuuur	r
∂z	=	∂z cosα							(7.12)
					+ ∂z cosβ = grad z			l .
∂l		∂x			∂y

94

Аналогично определяется производная по направлению и градиент

функции трех переменных u = f (x; y; z) :

∂u

= ∂u cosα

+ ∂u cos β +

∂u cosγ ;

∂l

∂x

∂y

∂z

uuuuuur

∂u ;

∂u ;

∂u

r

∂u

r

+

r

grad u

=

=

∂u i +

j

∂u k .

∂x

∂y

∂z

∂x

∂y

∂z

Градиент функции характеризует направление и величину наибыстрейшего роста функции в данной точке. Понятия производной по направлению и градиента функции играют важную роль во многих приложениях.

Метод наименьших квадратов

На практике мы часто сталкиваемся с задачей сглаживания экспериментальных зависимостей. Пусть зависимость между двумя переменными x и y выражается в виде таблицы.

x1	x2	…	xi	…	xn
y1	y2	…	yi	…	yn

Эти данные могут быть получены в результате опытных измерений или статистических наблюдений. Требуется наилучшим образом сгладить зависимость между переменными x и y, т.е. по возможности точно отразить общую тенденцию зависимости y от x, исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений. Такую сглаженную зависимость стремятся представить в виде формулы y=f(x), или, как говорят, аппроксимировать опытные данные функцией f(x).

Формулы, служащие для аналитического представления опытных данных, получили название эмпирических формул. Выбор той или иной эмпирической формулы основывается, как правило, на различного рода теоретических предпосылках. Обычно полагают, что множество допустимых функций является однопараметрическим семейством функций φ(x,α), где α –

какой-то набор параметров. Например, семейство гипербол: y = a + bx ,

семейство показательных функций y = ea+bx+cx2 и т.д. Задача аппроксимации

состоит в том, чтобы так подобрать параметры функции, чтобы она "наилучшим" образом отвечала исходным данным. Существует много способов определения неизвестных параметров, наиболее распространенным и теоретически обоснованным способом является метод наименьших квадратов.

Предположим, что функциональная зависимость между переменными x и y известна из предварительных сведений и имеет вид

y =ϕ(x;α0 ,α1,K,αk −1) ,

где α0, α1, …, αk–1 – неизвестные параметры, которые следует найти.

Метод наименьших квадратов состоит в том, что в качестве параметров α0, α1, …, αk–1 выбирают такие значения, чтобы сумма

95

квадратов отклонений "теоретических" значений φ(xi) от соответствующих значений yi была минимальной:

n
Q(α0 ,α1,K,αk −1) = ∑[yi −ϕ(xi ;α0 ,α1,K,αk −1 )]2 .	(7.13)

i=1

Необходимым условием минимума функции (13) будет равенство нулю всех частных производных этой функции. В результате, для нахождения параметров α0, α1, …, αk–1 нужно решить систему k уравнений:

		∂Q		= 0,
		∂α0
						(7.14)
LLLL
		∂Q
	∂α		= 0.
			k −1

7.2.Решение типовых примеров и задач

Пример 1. Найти все частные производные 1-го порядка

функций:

а) z = e2 xy +sin x2 +

1

; б)

z =

cos y 2

; в)

z =(cos x)y2 .

3

y5

x

Решение. а) Найдем частную производную функции

z = e2 xy +sin x2 +

1

по переменной x. Считая y постоянной, получим:

y5

3

∂z = e2 xy +sin x2 +

1

′ =

(

e2 xy

)x

′ +

(

sin x2

′ +

1

′ = e2 xy (2xy) ′ +

∂x

3

y

5

)x

3

y

5

x

x

x

+cos x2 (x2 )x′ + 0 = e2 xy 2 y + cos x2 2x = 2(ye2 xy + x cos x2 ).

1

Найдем частную производную функции z = e2 xy

+sin x2 +

по

3

y5

переменной y. Считая x постоянной, получим:

∂z

1

′

=(e2 xy )

′ +

(sin x2 )

′

−5

′

= e2 xy (2xy) ′

= e2 xy

+sin x2 +

+ y

3

+0

+

∂x

3

y

5

y

y

y

y

y

5

−

5

−1

2 xy

5

−8

2 xy

5

+

−

3

y

3

= e

2x −

3

y

3 = 2xe

−

.

y8

33

б) Найдем частную производную функции z = cosxy 2 по переменной x.

Считая y постоянной, получим:

96

∂z

cos y2

′

2 1

′

2

1

cos y2

= cos y

= cos y −

2

= −

2 .

∂x

=

x

x

x

x

x

x

Найдем частную производную функции z =

cos y2

по переменной y.

x

Считая x постоянной, получим:

∂z

cos y2

′

1

2

′

1

2

2ysin y2

=

(cos y

)y

=

(−sin y ) 2y = −

.

∂y

=

x

x

x

x

y

в) Найдем частную производную функции z =(cosx)y2 по переменной x. Считая y постоянной, получим:

∂∂xz =((cos x)y2 )x′ = y2 (cos x)y2 −1 (cos x)x′ = y2 (cos x)y2 −1 (−sin x)= = −y2 sin x(cos x)y2 −1 .

Найдем частную производную функции z =(cosx)y2 по переменной y. Считая x постоянной, получим:

∂z =((cos x)y2 )′ =(cos x)y2 ln(cos x)(y2 ) ′ =(cos x)y2 ln(cos x)(2y)=

∂y y y

= 2y(cos x)y2 ln(cos x).

Пример 2. Найти все частные производные 2-го порядка функции z = cosxy2 .

Решение. В примере 1 были найдены частные производные 1-го поряд-

ка этой функции:

∂z

cos y2

∂z

= −

2ysin y2

= −

и

. Найдем частные производ-

∂x

x2

∂y

x

ные от этих производных, т. е. частные производные 2-го порядка.

Найдем частную производную второго порядка по переменной x:

∂2 z

∂

∂z

cos y2 ′

2

1

′

2

−

2

2cos y2

z′′

=

=

=

−

= −cos y

= −cos y

=

.

2

2

2

3

3

xx

∂x

∂x ∂x

x

x

x

x

x

x

Найдем частную производную второго порядка по переменной y:

∂

2

z

∂

2ysin y

2

′

2

(ysin y2 ) ′

z′′

=

=

∂z

=

−

= −

=

2

yy

∂y

x

x

y

∂y

∂y

y

= −

2

(sin y2

+ y cos y2

2y)= −

2(sin y2 + 2y2 cos y2 )

.

x

x

Найдем смешанную частную производную второго порядка:

97

z′′

∂2 z

∂

∂z

cos y2

′

1

(cos y

2

)

′

1

(−sin y

2

2y)=

2ysin y2

.

=

=

=

−

= −

= −

∂x∂y

x2

x2

x2

x2

xy

∂y

∂x

y

y

Пример 3. Найти

∂z

и ∂z , если

x3 +cos y + z2 = 0;

∂x

∂y

Решение. В данном примере функция z = f (x; y)

задана неявно урав-

нением F(x; y;z) = 0 .

Сначала найдем

∂F

и

∂F

∂F

∂x

∂z

=(x3 +cos y + z2 )

′ =(x3 ) ′ +(cos y)x′

+(z2 )

′ =3x2 +0 +0 =3x2 ;

∂x

x

x

x

∂F

=(x3 +cos y + z2 )z′ =(x3 )z′ +(cos y)z′

+(z2 )z′ = 0 +0 + 2z = 2z .

∂z

Найдем частную производную функции по переменной x, воспользовавшись формулой (7.4):

	∂z	= −	∂F		∂x		= −	3x2	.
	∂x		∂F		∂z			2z
	Найдем			∂F		:
	∂F			∂y
		=(x3 + cos y + z2 )y′ = (x3 )y′ +(cos y)y′ +(z2 )y′ = 0 −sin y + 0 = −sin y .
	∂y

Найдем частную производную функции по переменной y, воспользовавшись формулой (7.4):

∂z

= −

∂F

∂y

= −

−sin y = sin y .

∂y

∂F

∂z

2z

2z

Пример 4. Найти

∂z

и

∂z

, если

e

x3y

+5ln z + x

4

= 0.

∂x

∂y

Решение. Найдем частную производную функции по переменной x, воспользовавшись формулой (7.4):

∂∂Fx =(ex3 y +5ln z + x4 )x′ =(ex3 y )x′ +(5ln z)x′ +(x4 )x′ = ex3 y (x3 y)x′ +0 + 4x3 = = ex3 y y 3x2 + 4x3 = x2 (3yex3 y + 4x);

∂∂Fz =(ex3 y +5ln z + x4 )z′ = (ex3 y )z′ +(5ln z)z′ +(x4 )z′ = 0 +5 1z + 0 = 5z ;

98

	∂z	= −	∂F ∂x	= −	x2 (3yex3 y + 4x)	= −	x2z(3yex3 y + 4x)	.
	∂x		∂F ∂z		5 z		5

Найдем частную производную функции по переменной y, воспользовавшись формулой (7.4):

	∂F	=(ex3y +5ln z + x4 )				′ =(ex3y )′ +(5ln z)y′ +(x4 )y′ = ex3y (x3 y)y′ +0 +0 = x3ex3 y
	∂y				y		y
	;
		∂z	= −	∂F ∂y	= −	x3ex3 y	= −	x3zex3 y			.
		∂y		∂F ∂z		5 z		5
		Пример 5. Найти дифференциалы 1-го и 2-го порядков и проверить ра-
			′′	′′					xy
	венство zxy			= zyx для функции				z = e			.

Решение. Найдем частные производные 1-го порядка этой функции: z′x = ∂∂xz = (exy )′x = exy y = yexy ;

z′y = ∂∂yz = (exy )′y = exy x = xexy .

Используя формулу (5), найдем дифференциал 1-го порядка:

dz =

∂z dx +

∂z dy = yexy dx + xexy dy = exy (ydx + xdy).

∂x

∂y

Найдем частные производные 2-го порядка:

∂2 z

xy

′

2

xy

′′

(ye )x = y e ;

= ∂x2 =

zxx

′′

∂2 z

xy

′

xy

xy

xy

zyx =

= (xe

)x

= e

+ xye

= e

(1+ xy);

∂y∂x

′′

∂2 z

= (ye

xy

)y

′

xy

xy

xy

zxy

=

= e

+ xye

= e

(1+ xy);

∂x∂y

z′yy′ = ∂∂y2 2z = (xexy )y′ = x2exy .

Отметим, что справедливо равенство z′xy′ = z′yx′ .

Используя формулу (6), найдем дифференциал 2-го порядка:

d

2

z =

∂2 z

dx

2

+ 2

∂2 z

dxdy +

∂2 z

dy

2

= y

2

e

xy

dx

2

+ 2e

xy

(1+ xy)dxdy + x

2

e

xy

dy

2

=

∂x2

∂x∂y

∂y

2

= exy (y2dx2 + 2(1+ xy)dxdy + x2dy2 .

Пример 6. Исследовать функцию на экстремум:

u = 2x3 + xy2 +5x2 + y2 .

99

Решение. Найдем стационарные точки данной функции, для этого вычислим частные производные функции и приравняем их нулю (условие

(7.9)):

∂∂u =x∂u =∂y

6x2 + y2 +10,		2	+ y	2	+10	= 0,
	6x
2xy +2 y.	2xy +2 y = 0.

Решая эту систему уравнений, находим, что существует четыре
стационарных точки:		5
	−
M1 (0; 0), M2		3	; 0 , M3 (−1; 2), M4 (−1; −2).
Теперь определим, есть ли в этих стационарных точках экстремумы.
Для этого вычислим A11, A22, A12 и ∆. Поскольку

∂2u

∂2u

∂2u

2

A =

∂x2

=12x +10,

A =

∂y2

= 2x + 2, A

=

= 2 y, = A A

− A

,

∂x∂y

11

22

12

11 22

12

то для вычисления этих коэффициентов в найденных стационарных

точках составим таблицу:

M1

M2

M3

M4

A11

10>0

–10<0

–2

–2

A22

2

–4/3

0

0

A12

0

0

4

–4

∆

20>0

40/3>0

–16<0

–16<0

min

max

экстремума нет

экстремума нет

Таким

образом, в точке M1(0; 0) функция имеет минимум, в точке M2(–

5/3; 0) – максимум, в точках M3 и M4 экстремума нет.

Пример 7. Найти наименьшее и наибольшее значения функции

y

z = x2 +3y2 − x − y в области, ограниченной

линиями x = 0, y = 0, x + y =1.

C

Решение. Изобразим область,

ограниченную данными прямыми. Искомая

1

область – треугольник ОAC (рис. 7.2).

M1

1) Определим стационарные точки:

А

а) Найдем частные производные

∂z

O

1

x

=(x

2

+3y

2

′

= 2x −1;

∂x

− x − y)x

Рис. 7.2

.

∂z

=(x2

+3y2 − x − y)y′ = 6 y −1.

∂y

б) Решая систему, найдем стационарную точку

100

						1
	2x −1= 0,			x =		2	,					1			1
										M1				;			.
															6
	6y −1= 0.					1	.					2
				y =		6
	Эта стационарная точка принадлежит рассматриваемой области (см.
	рис. 7.2). Найдем значение функции в данной точке:
		1		1		1		1				1		1				1
	z(M1) = z		;		=		+				−		−			= −			.
		2		6		4		12				2		6				3

2) Исследуем функцию на границе области.

а) При x=0 (отрезок ОС) имеем z=3y2-y, y [0;1]. Эта функция имеет

		y =	1		1			1
	минимум при			, z			= −			( для нахождения минимума найдем произ-
			6		6			12

	водную dz	и приравняем ее к нулю:		6y −1= 0; y =	1 ) и на концах отрезка
	dy				6
	принимает значения z(0) = 0, z(1) = 2. Таким образом, на отрезке AB наи-
						1		1
	большее значение		z(1) = 2 и наименьшее значение z				= −			.
						6		12

		б) При y=0 (отрезок ОА) имеем z=x2–x, x [0;1]. Эта функция имеет ми-
	нимум при x =			1		1		1
					, z	2	= −	4	( для нахождения минимума найдем производ-
				2
		dz
	ную		и приравняем ее к нулю: 2x −1= 0; x =							1 ) и на концах отрезка при-
		dx								2

нимает значения z(0) = 0, z(1) = 0. Таким образом, на отрезке BC наибольшее

	значение z(1) = z(0) = 0 и наименьшее значение								1		1	.
								z	2	= −	4
	в) При y=1–x (отрезок CA) имеем z=4x2–6x+2, x [0;1]. Эта функция
	имеет минимум при x =	3		3		1
			, z		= −		( для нахождения минимума найдем
		4		4		4

производную dxdz и приравняем ее к нулю: 8x −6 = 0; x = 34 ) и на концах от-

резка принимает значения z(0) = 2, z(1) = 0. Таким образом, на отрезке CA

							3			1
наибольшее значение z(0) = 2 и наименьшее значение						z			= −		.
							4			4
												1
			3) Сравнивая все найденные значения, получаем, что zнаим							= −			в точке
		1		1								3
M1			;
		2		6	, zнаиб = 2 в точке С(0;1).

101

Пример 8. Найти градиент функции z = f (x; y) в точке M (x; y) и про- uuur

изводную по направлению вектора MM1 , если z = x2 −3xy + y2 ,

M (1;2), M1(4;5).

Решение. Воспользуемся определением градиента функции

uuuuuur

∂z

; ∂z . Найдем частные производные в точке M:

grad z =

∂x

∂y

∂z

=(x2

−3xy + y2 ) ′ = 2x −3y

M (1;2)

= 2 1−3 2 = −4;

∂x

x

∂z

= (x2

−3xy + y2 )y′ = −3x + 2y

M (1;2)

= −3 1+ 2 2 =1;

∂y

uuuuuur

∂z

; ∂z

=

(−4;1).

Подставим в формулу grad z

=

M

∂x

∂y

uuur

uuur

:

= (4 −1;5 − 2) = (3;3).

Найдем координаты вектора MM1

MM1

Найдем длину вектора

uuuur

=

32 +32 =

18 = 3

2 . Единичный вектор l в

MM1

uuuur

направлении вектора MM1 :

1

1

1

r

1

uuuur

l = (cosα

;cosβ) = uuuur

MM1

=

(3;3) =

;

. Для определения

3 2

2

MM1

2

uuuuur

производной по направлению найдем скалярное произведение вектора grad z и вектора lr:

∂z

uuuuuur

r

∂z

∂z

1

1

3

∂l

= grad z

l

=

∂x

cosα +

∂y

cosβ = −4

+1

= −

.

2

2

2

Пример 9. Методом наименьших квадратов подобрать функцию y = ax +b по табличным данным и сделать чертеж.

x	0	2	4	6	8	10	12
y	10	93	72	36	17	43	19
	80	5	4	2	6

Решение. В соответствие с методом наименьших квадратов следует подобрать коэффициенты a и b таким образом, чтобы функция

n

Q(a,b) = ∑(yi −axi −b)2

i=1

приняла минимальное значение. Необходимым условием экстремума функции Q является равенство нулю всех частных производных по неизвестным параметрам:

102

∂Q

n

= −2∑(yi − axi −b)xi = 0,

∂a

i=1

∂Q

n

∑

= −2

(y

− ax −b) = 0.

∂b

i

i

i=1

Упростим систему уравнений:

n

n

n

n

∑(yi − axi −b)xi = 0,

∑yi xi − a∑xi2 −b∑xi = 0,

i=1

i=1

n

i=1

i=1

n

n

−a∑xi − nb = 0.

∑(yi − axi −b) = 0,

∑yi

i=1

i=1

i=1

n

n

n

n

Обозначим:

A = ∑yi xi ; B = ∑xi2; C = ∑xi; D = ∑yi . Запишем сис-

тему и решим ее:

i=1

i=1

i=1

i=1

D − aC C = 0,

A − aB −bC

= 0,

A − aB −bC =

0,

A − aB −

D − aC

n

=

,

D

− aC

D − aC − nb = 0,

b

n

b =

n

,

C

DC + aC

2

2

− nB DC − An

A − aB −

=

0,

a

n

=

n

,

n

n

D −aC

D

−aC

b =

n

,

b =

n

,

DC − An

,

a =

DC − An

,

a =

C

2

− nB

C

2

− nB

DC2 − nDB − DC2

+ nAC

−DB + AC

,

.

b =

nC

2

− n

2

B

b =

C

2

− nB

Далее, составим таблицу вычислений:

№

x

y

yx

x2

1

0

1080

0

0

2

2

935

1870

4

3

4

724

2896

16

4

6

362

2172

36

5

8

176

1408

64

103

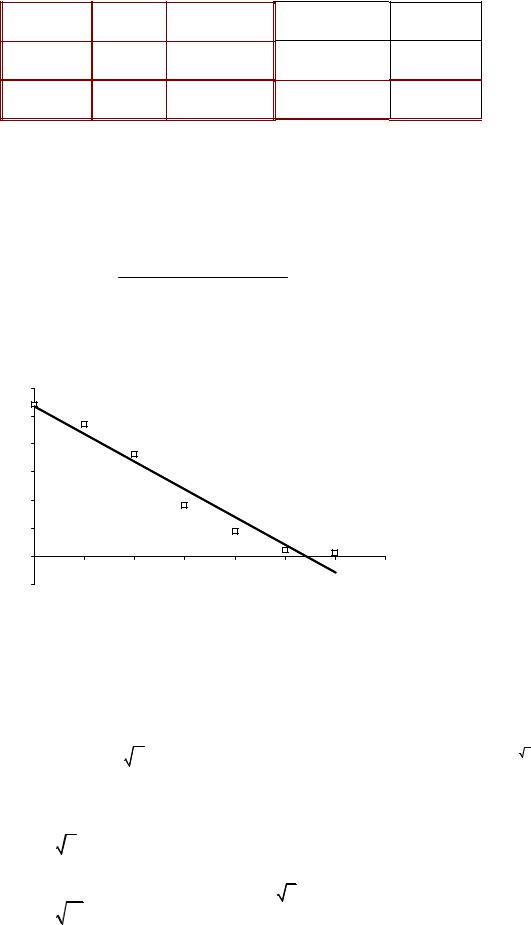
		6			10			43			430	100
		7			12			19			228	144
		∑			42			3339			9004	364
По таблице находим:
	n					n					n	n
A = ∑yi xi =9004; B = ∑xi2 =364; C = ∑xi = 42; D = ∑yi													=3339.
	i=1					i=1					i=1	i=1
a =	DC − An =			3339 42 −9004 7					= −98,48;
	C2 − nB				422	−7 364
	−DB + AC				−3339 364 +9004 42
				=						=1067,89.
b =	C	2	− nB			42	2	−7 364
Таким образом, искомая функция имеет вид: y = −98,48 x +1067,89 .
Изобразим на рис. 7.3 исходные данные (квадратики) и искомую пря-
мую:
1200
1000
800								y = -98,48x + 1067,89
600
400
200
	0
	0		2		4		6	8	10		12	14
-200
								Рис. 7.3
				7.3. Задания на контрольную работу

Задание 1. Найти все частные производные 1-го порядка:

1.

а) z = 2xy −tg x +

y,

б)

z =

cos(2x)

,

2.

а)

1+ y2

б)

z =

sin(y3 )

,

x3

1

z =

−ctg(xy) +

,

x4

6

y

3.

а)

1

б)

z =

tg(y4 )

,

z = ctg(xy) −ex2 +

,

x

y7

в) z = (1+ctg y) x .

в) z = (cos x)ln y .

в) z = (cos y)ln x .

104

4. а)

б)

z =

x4

1

,

z = ctg(xy) −

+e

−2 y2

,

cos3y

x

5. а)

б)

z =

e1/ x

,

z = x7 −cos(2xy) +

y3 ,

y2

6. а)

z = exy

+ tg x3 + 4 y,

б)

z =

ln(1+ y

2 )

,

7. а)

x

6

y

1

б)

z =

sin

y

,

1+ x

z =

−ctg

+

,

x3

x

y5

8. а)

−y2

б)

z =

1+ x3

,

1

cos6y

z = tg(4xy) −

+e 4 ,

9. а)

x3

sin(4x)

б)

z =

,

z = xy2 −tg

x

+ y7 ,

y2 −4

3

10. а)

1

б) z = ctg(x5 ) ,

3

y2

z =sin(xy) + x5 +lg y,

в) z = (1−3y )ln x .

в)	z = (cos x)ctg y .
в)	z = (sin y)x2 .
в)	z = (cos2x)1/ y .
в)	z = (ln x)sin y .
в)	z = (ctg x) y .

в) z = (1+ln x)1/ y .

Задание 2. Найти ∂z и

∂z , если

∂x

∂y

1.

x2 −4y2 + z2 +6x = 0 ;

2. exy +4cos x + z2 = 0 ;

3.

x2 − tg y +cos z +10x = 0;

4. exy3

+ 4sin z + x2

= 0 ;

5.

x3 +5y2 + z2 +8y = 0;

6. exy

+5sin x + z3 = 0 ;

7.

x2 +ln y +sin z +9x = 0;

8. ex2 y −6cos z + x3

= 0 ;

9.

x3 −ctg y +cos z + 2y = 0 ;

10. exy2 +3ln x + z3 = 0.

Задание 3. Найти дифференциалы 1-го и 2-го порядков и проверить ра-

′′

′′

венство zxy

= zyx для функции z = f (x; y) :

2

1.

z = e2x/ y ;

2.

z = sin

x

;

3.

z = ln (x2 + 4y4 );

y

5.

x

4.

z = y −sin(xy) ;

z =sin 1−

;

6.

z = ysin(3x −5y) ;

y

7.

z = e1−x/ y ;

8.

z = sin (x2 y);

9.

z = ln (3x4 + y5 );

10. z = y +cos(xy) .

Задание 4. Исследовать функцию на экстремум:

1.

z = 2x3 − xy2 +5x2 + y2 ;

2. z = x3 + y3 −15xy ;

105

3.	z = x3 +3xy2 −15x −12;	4.	z = x3 +8y3 −6xy +5;
5.	z = x3 + xy2 +6xy ;	6.	z = x3 + y3 +3xy ;
7.	z = x3 + y3 −3xy ;	8.	z = x3 + xy2 +3xy ;
9.	z =3x2 − x3 +3y2 + 4y;	10. z = x3 − y3 −12xy .

Задание 5. Найти наименьшее и наибольшее значения функции:

1.z =6xy − x2 y − xy2 в области, ограниченной линиями x=0, y=0,

x+y=12;

2.z = x2 + 2xy −4x +8y в области, ограниченной линиями x=0, y=0, x=

–5, y=7;

3.z = x2 −2y2 +5 в области, ограниченной линиями x=1, y= –1, x–

y+1=0;

4. z = xy + x + y в области, ограниченной линиями x=0, x= –2, y=0, y=

–2;

5.z = x2 +3y2 + x − y в области, ограниченной линиями x= –1, y=0,

x+y=1;

6.z = x2 + 4xy −2x + 4y в области, ограниченной линиями x=0,y=0, 3x–2y+6=0;

7.z = x2 +2y2 + x −2y в области, ограниченной линиями x= –1, y=1,

2x–2y= –1;

8.z = 5xy +10x − y +1 в области, ограниченной линиями x=0, x=1, y= –

3, y= –1;

9.z = x2 − xy + y2 −4x в области, ограниченной линиями x=0, y=0,

2x+3y–12=0;

10. z = x2 −4xy − y2 +4x в области, ограниченной линиями x=0, 4x–y+4=0.

Задание 6. Найти градиент функции z = f (x; y) в точке M (x; y) uuur

изводную по направлению вектора MM1 , если

1.z = x3 −3xy + 2y2 , M (1;1), M1(4;6) ;

2.z =3x2 −2xy + 2y3 , M (−1;1), M1(4;2);

3.z =5x2 −4xy + y2 , M (1;−1), M1(−4;3);

4.z =3x3 + 2xy + y3 , M (1;1), M1(4;3);

5.z = x3 +3x2 y + y2 , M (2;1), M1(5;6) ;

6.z = 2x3 +4xy2 + y2 , M (2;2), M1(4;−6);

7.z =7x2 + xy +6y2 , M (1;1), M1(−2;−1);

y=0,

и про-

106

8.z = x3 +4xy2 +2y2 , M (1;1), M1(−2;−2);

9.z = x3 + x2 y −3y2 , M (−1;2), M1(3;3);

10.z =5x2 +4xy −7y , M (1;−2), M1(3;5) .

Задание 7. Методом наименьших квадратов подобрать функцию y = ax + b по табличным данным и сделать чертеж.

1.	x	0	1	1,5	2,1	3
	y	2,9	6,3	7,9	10,0	13,2
2.	x	0	3	6	9	12
	y	0,3	4,1	5,7	13,4	28,5
3.	x	1	2	3	4	5
	y	11,2	9,2	7,9	4,1	2,5
4.	x	1	3	5	7	9
	y	14,1	12,5	9,7	4,6	0,3
5.	x	0	0,5	1	1,5	2
	y	1,2	3,5	4,1	8,5	14,9
6.	x	2	4	6	8	10
	y	7,2	17,3	25,4	38,1	55,6
7.	x	0	0,5	1	1,5	2
	y	1,1	2,3	9,7	16,2	25,4
8.	x	1	4	7	10	13
	y	17,2	8,7	5,6	4,5	3,5
9.	x	1	3	5	7	9
	y	2,1	9,8	13,7	14,5	15,2
10.	x	1	4	7	10	13
	y	23,7	12,5	10,1	8,8	7,1

107