Оценка нормальности вариационных рядов

Результат медико-биологического эксперимента или отдельного клинического наблюдения называют вариантой (х), а набор вариант, расположенный в возрастающем (убывающем) порядке – вариационным рядом.

х₁, х₂, …, х_i, … , х_n

где n – количество наблюдений (длина вариационного ряда).

Основными параметрами, которые характеризуют вариационный ряд являются:

1. Величины, которые в зависимости от обстоятельств принимают те или иные значения, называются случайными величинами. Они могут быть непрерывными (измерения объема грудной клетки) или дискретными (количество очков выпавшее на игральной кости).

2. Вероятность наступления события – отношение числа исходов благоприятствующих наступлению данного события (m) к числу всех возможных исходов испытания (n):

Для дискретной случайной величины .

3. Математическое ожидание (среднее значение) случайной величины – сумма произведений всех возможных ее значений на вероятности этих значений:

4. Дисперсия случайной величины – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

5. Среднее квадратическое отклонение – квадратный корень из дисперсии (вводят для оценки рассеяния случайной величины в единицах той же размерности):

Полный набор всех вариант есть генеральная совокупность. На практике, как правило, невозможно получить все варианты генеральной совокупности, поэтому исследуется выборочная совокупность.

Самым распространенным распределением в природе, экономике и т.д. является нормальное распределение. Случайная величина с нормальным распределением может принимать любые значения в интервале от - до + и имеет функцию плотности вероятности:

где а – математическое ожидание случайной величины;  - среднее квадратическое отклонение; ² – дисперсия случайной величины

Кривая нормального распределения имеет колоколообразную форму (рис. 1), симметричную относительно прямой х=а (центр рассеивания). В точке х=а функция достигает максимума: и образует перегибы в точках х₁=а- и х₂=а+ (рис. 2).

По мере возрастания х–афункция монотонно убывает, асимптотически приближаясь к нулю. При изменении значения  изменяется вид графика: при увеличении значения  в m раз максимальное значение функции уменьшается в m раз и график "вытягивается" в обе стороны вдоль оси х=а. При уменьшении значения  происходит обратное. При изменении значения а график функции f(x) смещается вдоль оси (рис.1).

	Для кривых: a1=0, а2=0, а30; 12, 2=3
Рис. 1.		Рис. 2

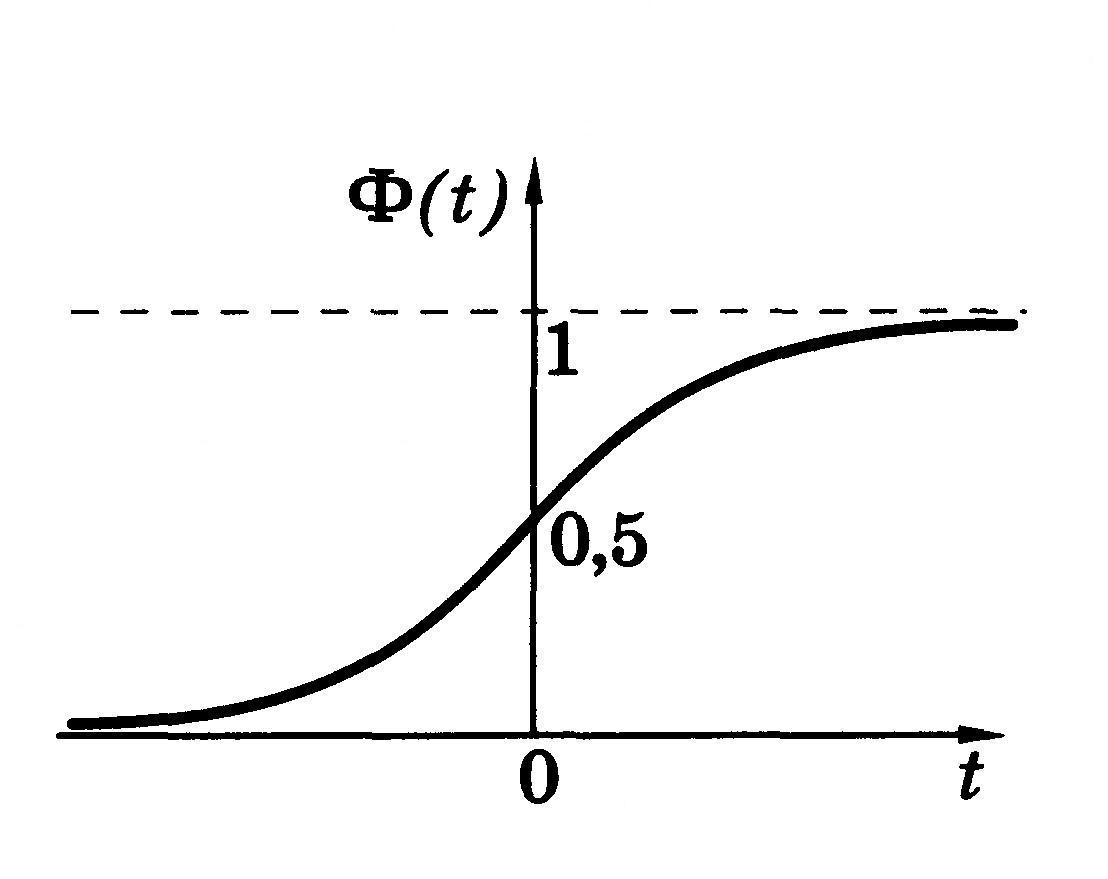
Наряду с плотностью вероятности используют так же функцию распределения непрерывной случайной величины:

На основании формул (1) и (2) получаем функцию распределения:

Введем новую переменную и получим

Рис. 3.

Значения функции Ф(t) приведены в соответствующих таблицах. График функции изображен на рис. 3.

;>.

На основании выражения можно вычислить вероятность того, что случайная величина при нормальном распределении находится в интервале (х₁, х₂):

Р(х₁хх₂)

Это выражение можно использовать для расчета вероятности нахождения случайной величины в интервалах а, а2, а3. Расчет показывает, что величина вероятности составляет: Р=0,68268 (для а); Р=0,95450 (для а2) и Р=0,99730≈1 (для а3). Таким образом, случайная величина X с нормальным распределением практически не принимает значений, которые отличались бы от среднего значения по абсолютной величине больше чем на 3. Это утверждение называется правилом "трех сигм" (рис. 2).

Как и другие законы распределения нормальный закон Гаусса не является беспредметной абстракцией, а представляет математическое выражение реальных закономерностей, существующих в массовых случайных явлениях. В частности, многие величины в биологии и медицине распределены по нормальному закону.

Закону Гаусса подчиняются:

– рост и вес взрослых людей;

– верхнее артериальное давление крови при исследовании большого контингента пациентов;

–длина сосудов, размеры органов, вес и объем мозга, определенные при массовых анатомических обследованиях;

– абсолютные ошибки показания приборов, измерений;

– содержание ферментов у здоровых людей.

Указанные примеры составляют незначительную часть от всего многообразия случайных биологических величин, подчиняющихся нормальному закону распределения.

Распределение Гаусса является распределением, к которому в соответствии с законом больших чисел при неограниченном увеличении числа испытаний стремятся (сводятся) все законы распределения. В этом случае применение закономерностей нормального распределения теоретически обосновано и в вопросах медицинской статистики, когда число объектов велико, расчет статистических данных в предположении о нормальности распределения исходного материала является правомерным.

В лабораторных условиях и в клинических исследованиях число испытуемых объектов, как правило, невелико, поэтому утверждение о нормальном распределении полученного экспериментального материала требует строгого математического обоснования. Тем более что применение статистических критериев Стьюдента, Фишера и т.д., расчет корреляционных и регрессионных параметров и многие другие методы математической статистики базируются на предположении о нормальном распределении исходных вариационных рядов.

Существуют различные методы оценки нормальности распределения результатов наблюдений.

ГОСТ рекомендует для проверки нормальности распределения группы результатов пользоваться критерием Пирсона, критерием Мизеса-Смирнова, а также составными критериями.

Самым распространенным является критерий согласия Пирсона, который применяется всегда, когда требуется определить степень различия между фактическим распределением и теоретическим, в частности, нормальным распределением.

Сущность метода сравнения экспериментального вариационного ряда и соответствующего ему нормально распределенного ряда состоит в том, что строится теоретический нормально распределенный ряд с параметрами исходного ряда, т.е. математические ожидания (М(Х) или Х) и среднеквадратические отклонения () экспериментального и теоретического рядов равны.

Далее определяется величина ² (хи-квадрат) по формуле:

,

где n_j – частоты экспериментального вариационного ряда; n'_j – теоретические частоты; k – число классов вариант.

Для нормального распределения с параметрами X и  теоретические частоты равны:

n – длина вариационного ряда;  - величина классового интервала; – нормированное отклонение середины j-го интервала;

Далее возникает вопрос: как велика может быть величина ², чтобы пренебречь различием между рядами?

Для ответа на этот вопрос пользуются таблицей предельных значений ² (таблица 1), которые зависят от уровня значимости критерия Р и числа степеней свободы, которые при сравнении с нормальным распределением равно k–3

Если при заданном уровне значимости и соответствующем числе степеней свободы ²<²_теор то считают, что отклонение экспериментального распределения от нормального незначительно и далее можно считать экспериментальные данные нормально распределенными. В общем случае оценка нормальности распределения данного вариационного ряда состоит из следующих этапов:

1. Вычислить среднее арифметическое X и среднеквадратическое отклонение  данного ряда;

2. Варианты данного вариационного ряда разбить на классы и определить экспериментальные частоты (n_j);

3. Рассчитать частоты теоретического нормального распределения (n'_j) с основными параметрами X и ;

4. Вычислить значение критерия ² и сравнить с табличным (²_теор).

Прежде чем приступать к решению задачи, рассмотрим пример. Из партии резисторов, имеющих приблизительно одинаковое сопротивление взяли наугад 50 шт и измерили точно их сопротивление.