Данные измерения 50 сопротивлений

N	[Ом]	N	[Ом]	N	[Ом]	N	[Ом]	N	[Ом]
1	820	11	843	21	842	31	809	41	810
2	833	12	806	22	803	32	802	42	827
3	835	13	795	23	820	33	823	43	840
4	821	14	811	24	819	34	824	44	818
5	824	15	821	25	803	35	851	45	834
6	795	16	823	26	847	36	832	46	811
7	837	17	839	27	847	37	803	47	821
8	835	18	826	28	807	38	809	48	826
9	843	19	832	28	812	39	819	48	827
10	822	20	804	30	834	40	807	50	830

1. Рассчитаем среднее арифметическое X и среднеквадратическое отклонение  для данного ряда с помощью с помощью программы Microsoft Exel. Введем значения в ячейки листа (например, А1–А50). Активируем курсором мыши пустую ячейку (например, А2). Выберем ВставкаФункция (или нажать иконку f_x). В строке Категория выберем Статистические, в окне Выберите функцию – СРЗНАЧ. Нажмите ОК. В появившемся окне в строке Число 1 необходимо указать массив значений (это можно сделать выделив мышью введенные значения – ячейки А1–А50). В нижней строке окна появится среднее арифметические значение для исследуемой выборки. При нажатии кнопки ОК эта величина сохранится в выбранной ячейке (А2). Активируем следующую пустую ячейку (например, В2) и повторим действия, выбрав в качестве расчетной функции СТАНДОТКЛОН.

КОНТРОЛЬНЫЙ ПРИМЕР 1:

Вычислить основные параметры вариационного ряда

15, 10, 12, 14, 12, 13, 11.

В результате расчета получаем:

X=12,42857≈12,4; =1,718249≈1,7.

В результате расчета получаем:

X=822,44; =14,38843

2. Для определения экспериментальных частот (n_j) составим статистический ряд, для чего запишем значения 50 сопротивлений в возрастающем порядке

R_j [Ом]

795	795	802	803	803	803	804	806	807	807
809	809	810	811	811	812	819	819	820	820
821	821	821	822	823	823	823	824	824	826
826	827	827	830	832	832	833	834	834	835
835	837	839	840	842	843	843	847	847	851

 Варианты данного вариационного ряда разбить на классы. Число классов вариант k определяется по формуле:

где n=50 – количество наблюдений, называемое длиной вариационного ряда.

Необходимая величина классового интервала () определяется по формуле:

Разбиваем диапазон значений 50 сопротивлений на 7 классов с величиной классового интервала 8. Данные заносим в таблицу 1.

Таблица 1.

k	xj min- xj max		Экспериментальные частоты nj	Плотность вероятности f	Теоретические частоты n'j
					точно	округленно
1	795-803	799	3	0,007	2,8	3
2	803-811	807	10	0,015	6	6
3	811-819	815	4	0,024	9,6	10
4	819-827	823	14	0,028	11,2	12
5	827-835	831	8	0,023	9,2	10
6	835-843	839	6	0,015	6	6
7	843-851	847	5	0,007	2,8	3
						50

 Рассчитать среднее значение для каждого интервала:

и т.д. Данные занести в таблицу 1.

 Определить экспериментальные частоты n_j, подсчитав количество вариант встречающихся в каждом интервале. Данные занести в таблицу 1.

 Рассчитать теоретическую плотность вероятности для каждого интервала (f) с помощью программы Microsoft Exel. Активируем курсором мыши пустую ячейку. Выберем ВставкаФункция (или нажать иконку f_x). В строке Категория выберем Статистические, в окне Выберите функцию – НОРМРАСП. Нажмите ОК. В появившемся окне:

– в строке Х необходимо указать среднее значение для интервала ();

– в строке Среднее – среднее арифметическое значение вариационного ряда (X);

– в строке Стандартное_откл – среднеквадратическое отклонение вариационного ряда ();

– в строке Интегральная – ввести слово "ложь". Программа в этом случае будет использовать для расчетов уравнение нормального распределения:

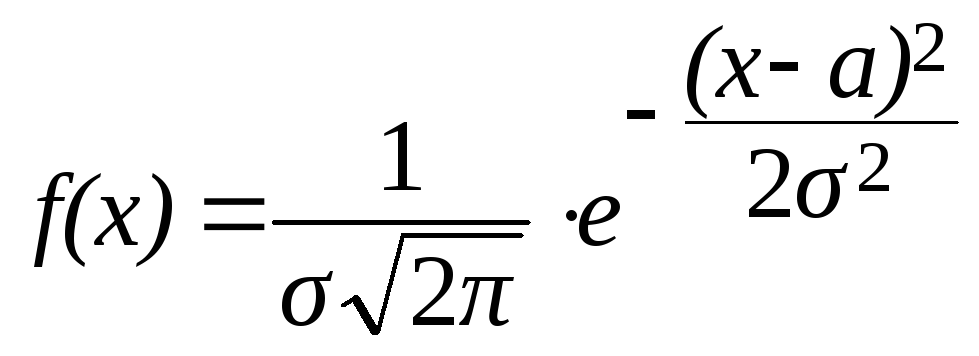
В нижней строке окна появится значение плотности вероятности для соответствующего интервала. Данные занести в таблицу 1, повторить операцию для всех интервалов, изменяя .

Теоретическая частота (n'_j) является произведением плотности вероятности (f) на объем выборки (n) и величину классового интервала ():

n'_j= f n

Провести соответствующие расчеты для каждого интервала, данные занести в таблицу 1.

ПРИМЕЧАНИЕ: расчетные значения теоретических частот округлять до целых значений, но сумма теоретических частот должна быть равна сумме экспериментальных частот.

КОНТРОЛЬНЫЙ ПРИМЕР:

Вычислить теоретические частоты для сгруппированного в 8 классов вариационного ряда:

n=100; =10; X=417; =13,5

j	1	2	3	4	5	6	7	8
	450	440	430	420	410	400	390	380
nj	1	7	20	30	25	10	6	1
f	0,001	0,007	0,019	0,029	0,026	0,013	0,004	0,001
n'j	1	7	19	29	26	13	4	1

 Вычислить значение критерия ² по формуле , где n_j – частоты экспериментального вариационного ряда; n'_j – теоретические частоты; k – число классов вариант. Для этого необходимо найти отношение квадрата разности экспериментальных и теоретических частот к теоретической частоте для каждого интервала и просуммировать их.

² = 8,33

Определить табличные значения ²_теор при Р=5% и n'_j=4 по таблице 2, где n' – число степеней свободы. Число степеней свободы определяется по формуле:

n' = k – 3

n' = 7 – 3 = 4

Таблица 2.

ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ КРИТЕРИЯ ПИРСОНА

n'	10%	5%	1%	n'	10%	5%	1%
1	2,7	3,8	6,6	16	23,5	26,3	32,0
2	4,6	6,0	9,2	17	24,8	27,6	33,4
3	6,3	7,8	11,3	18	26,0	28,9	34,8
4	7,8	9,5	13,3	19	27,2	30,1	36,2
5	9,2	11,1	15,1	20	28,4	31,4	37,6
6	10,6	12,6	16,8	21	29,6	32,7	38,9
7	12,0	14, 1	18,5	22	30,8	33,9	40,9
8	13,4	15,5	20,1	23	32,0	35,2	41,6
9	14,7	16,9	21,7	24	33,2	36,4	43,0
10	16,0	18,3	23,2	25	34,4	37,7	44,3
11	17,3	19,7	24,7	26	35,6	38,9	45,6
12	18,5	21,0	26,2	27	36,7	40,1	47,0
13	19,8	22,4	27,7	28	37,9	41,3	48,3
14	21,5	23,7	29,1	29	39,1	42,6	49,6
15	22,3	25,0	30,6	30	40,3	43,8	50,9

Табличное значение ²=9,5.

Из полученных данных имеем, что расчетное значение ² меньше табличного, т.е. 8,33<9,5 следовательно, можно считать распределение данного ряда нормальным.

построение "гистограммы плотности

исследуемой случайной величины

Для построения гистограммы:

– разбить диапазон значений сопротивлений на интервалы равной длины (в нашем случае 7 интервалов с длиной равной 8).

– подсчитать число наблюдений (вариант) попавших в каждый интервал.

– в каждом интервале определить относительную частоту , т.е. подсчитать количество наблюдений, находящихся в интервале j отнесенных к общему числу наблюдений.

– расчетные данные вариационного ряда для построения гистограммы плотности исследуемой величины занести в таблицу 3.

Таблица 3

Интервалы	795-803	803-811	811-819	819-827	827-835	835-843	843-851
nj	3	10	3	15	8	6	5
wj	3/50 0,06	10/50 0,2	4/50 0,08	14/50 0,28	8/50 0,16	6/50 0,12	5/50 0,1

На основании данных таблицы 3 построить гистограмму плотности исследуемой величины, т.е. построить на основаниях интервалов их плотности относительных частот. На оси абсцисс отложить точки деления интервала, а на оси ординат относительное число наблюдений, находящихся в интервале:

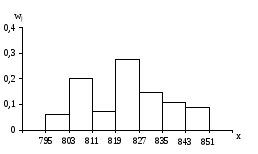
ПОСТРОЕНИЕ ЭМПИРИЧЕСКОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

ПО ДАННЫМ ПОЛУЧЕННОГО ВАРИАЦИОННОГО РЯДА

Эмпирическая функция распределения определяется как вероятность наблюдать x_j<x

,

где n_x –число наблюдений, при которых наблюдается значение признака меньше х, т.е. x_j<x; n – общее число наблюдений (объем выборки).

Алгоритм построения эмпирической функции распределения состоит в следующем:

– расположить вариационный ряд в порядке возрастания вариант;

– найти размах вариант, т.е. интервал, в котором заключены все значения вариационного ряда (в нашем случае 851-795=56);

– разделить этот интервал на равные части, число которых выбирают в зависимости от количества наблюдений (в нашем случае 8);

– подсчитать число наблюдений, находящихся "левее" каждой из точек деления интервала наблюдаемых величин – n_x (полученные данные занести в таблицу 4);

– подсчитать количество наблюдений, находящихся "левее" точки деления, отнесенных к общему числу наблюдений – (полученные данные занести в таблицу 4).

- на основании данных таблицы 4 построить график эмпирической функции распределения, откладывая на оси абсцисс точки деления интервала, а по оси ординат относительное число наблюдений.

Точки деления интервала	795	803	811	819	827	835	843	851
nx	0	3	13	16	31	39	45	49
	0/50 0	3/50 0,06	13/50 0,26	16/50 0,32	31/50 0,62	39/50 0,78	45/50 0,90	49/50 0,98