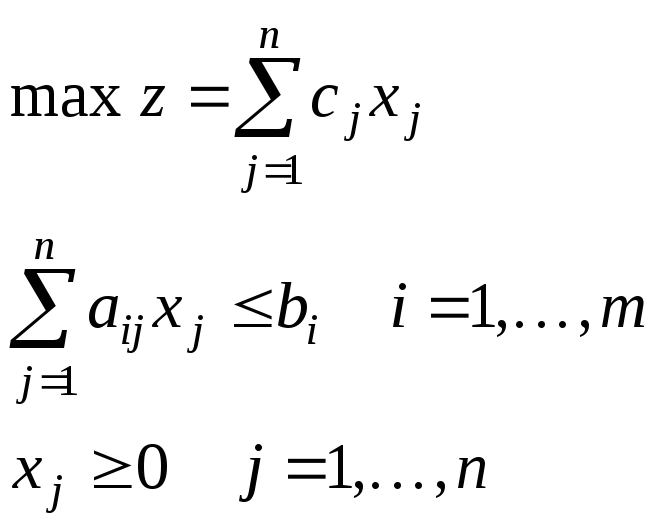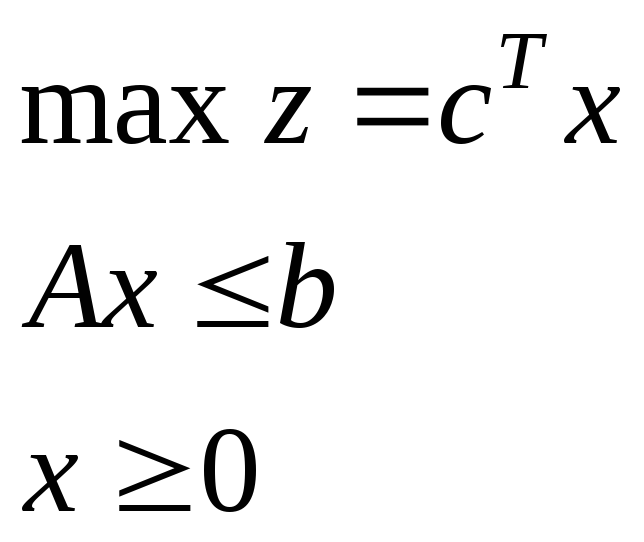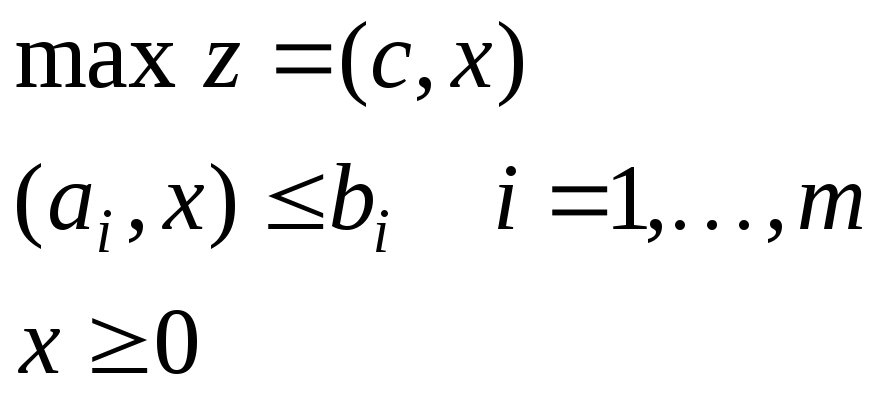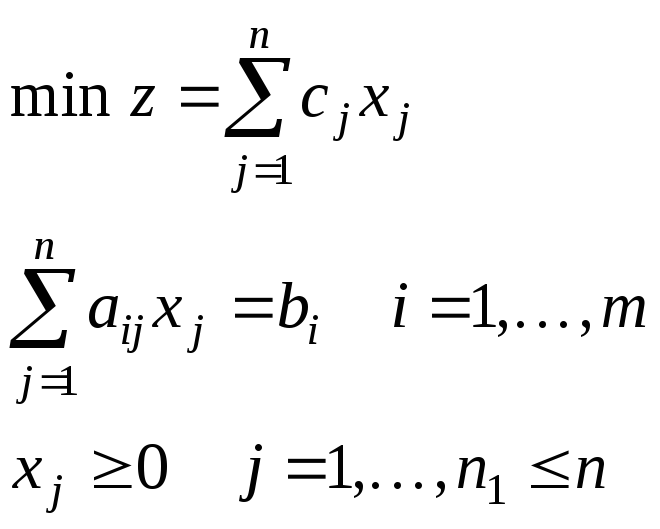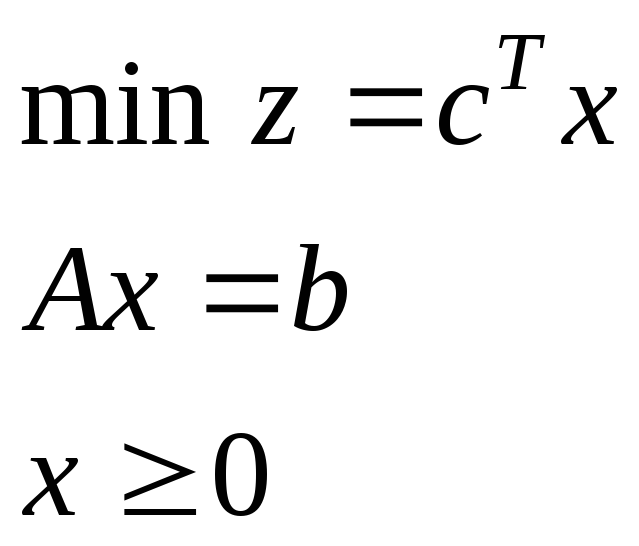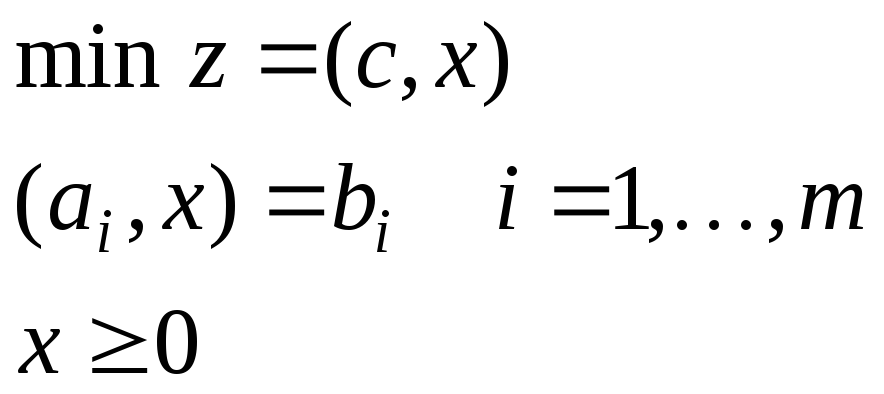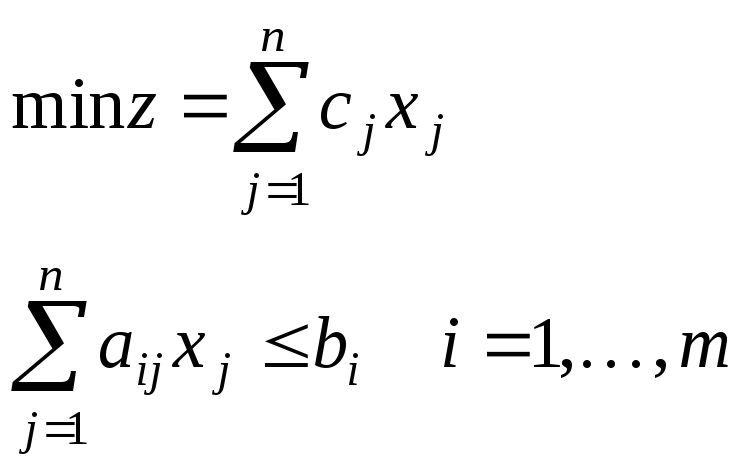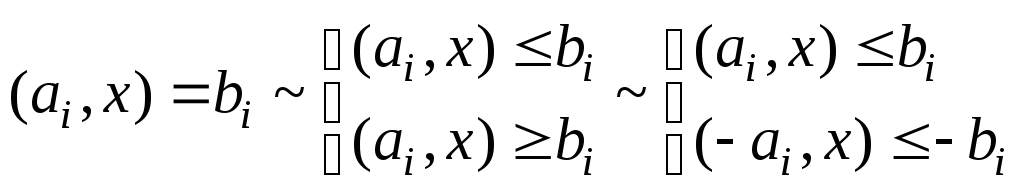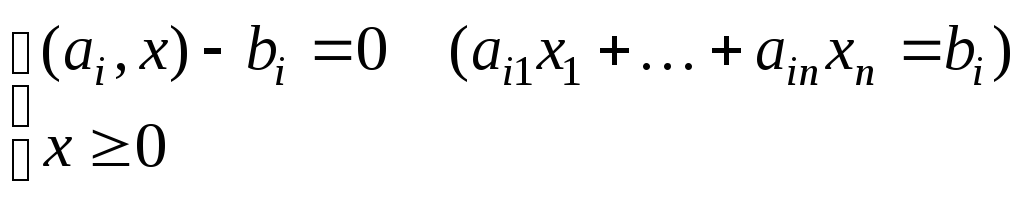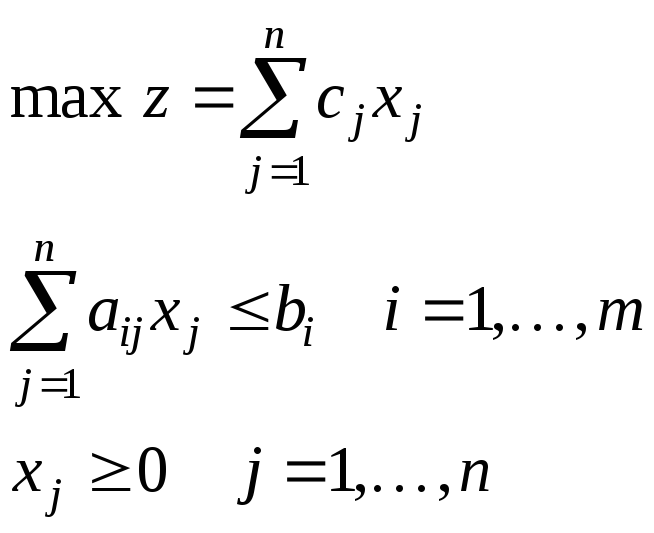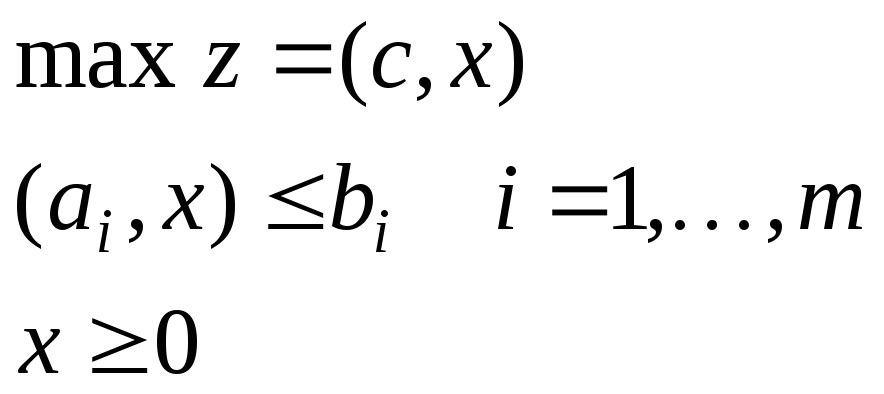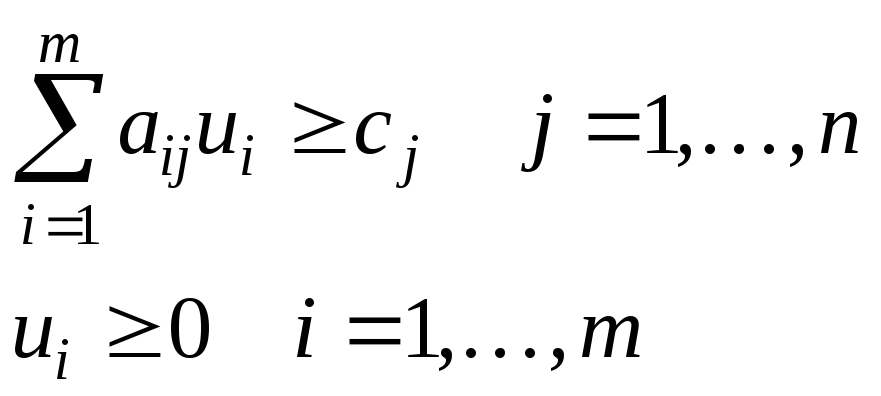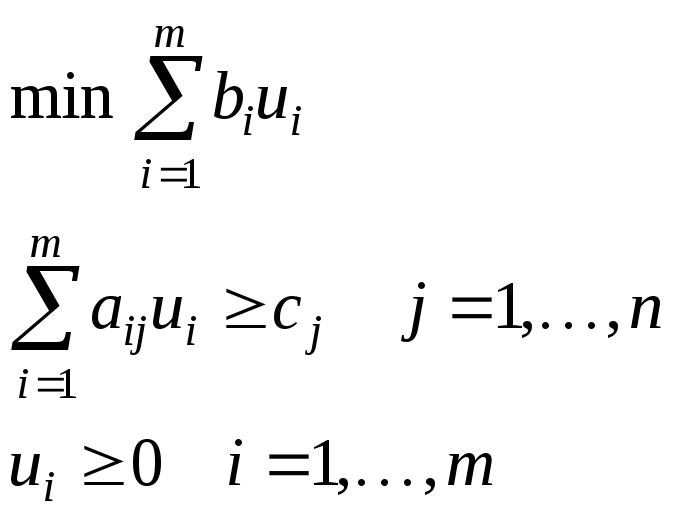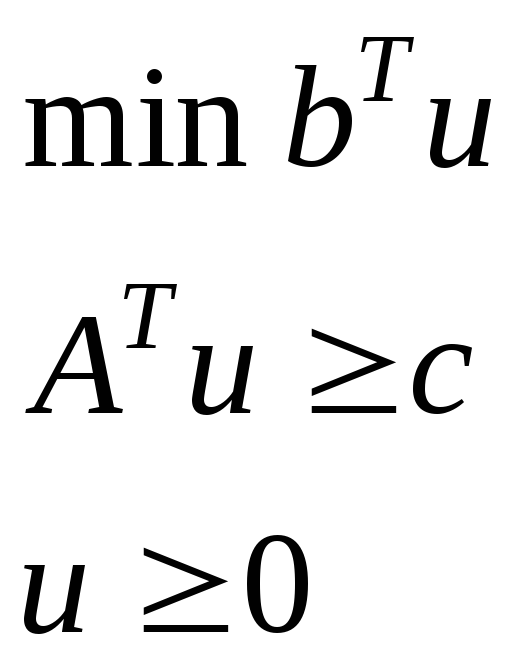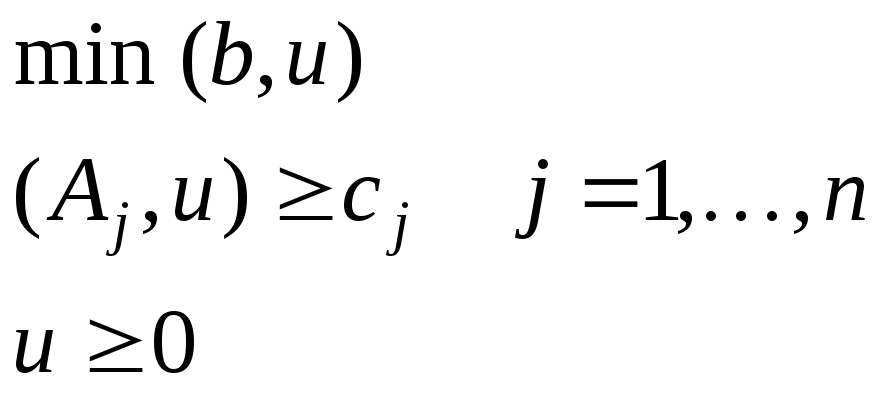I. Общая задача лп

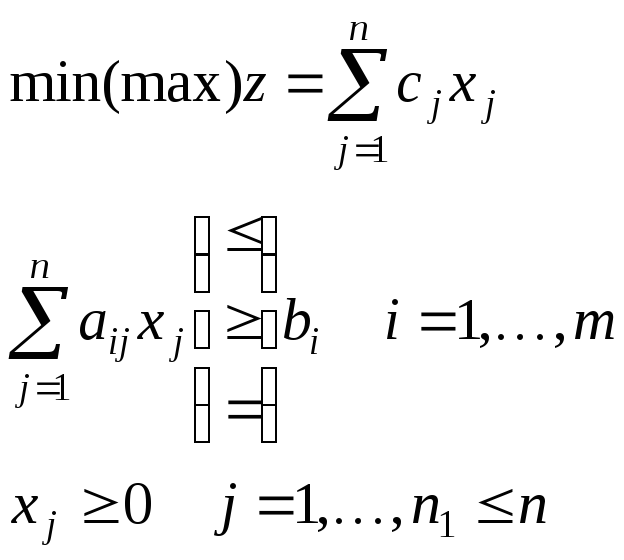
z – целевая функция

c= (c₁, …,c_n) – вектор целей

A= (a_ij)_mxn– матрица задачи (матрица условий)

b= (b₁, …,b_m) – вектор ограничений (вектор правых условий)

x= (x₁, …,x_n) – план задачи (решение задачи)

Условие x_j ≥ 0 – условие неотрицательности переменных

Множество x, удовлетворяющих всем ограничениям называется множеством допустимых решений, обозначаетсяX. План, на котором достигается оптимум целевой функции (минимум/максимум) называется решением задачи (оптимальный план), обозначаетсяx^*.X^*– множество решений задачи.

Решить общую задачу ЛП означает, найти хотя бы один оптимальный план и вычислить оптимальное значение.

Частные задачи ЛП

Скалярная форма	Матричная форма	Векторная форма
II. Стандартная задача ЛП (задача планирования производства)
III. Каноническая задача ЛП (транспортная задача)
IV. Основная задача ЛП

Все виды задач ЛП эквивалентны: существуют однозначные правила перехода от одного вида задачи к другому и решая последнюю задачу и вспоминая правила перехода, мы можем написать решение исходной задачи, не решая ее.

Правила перехода

1. 

2. 

3. 

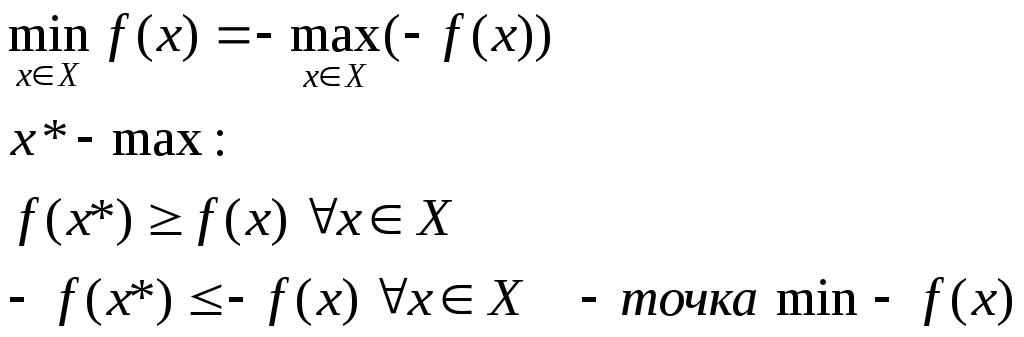
x_n+i– дополнительные переменные, (насколько недоиспользовано ограничение)

4. 

5. 

Пусть a_i1 ≠ 0

6. Пусть

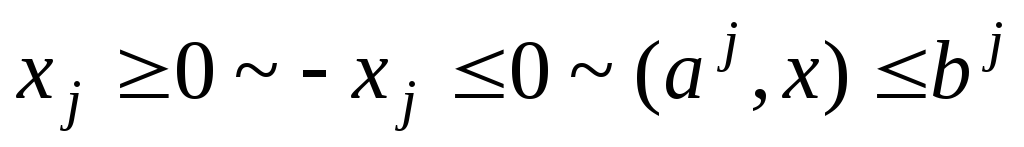
7. Пусть x_j– свободная ~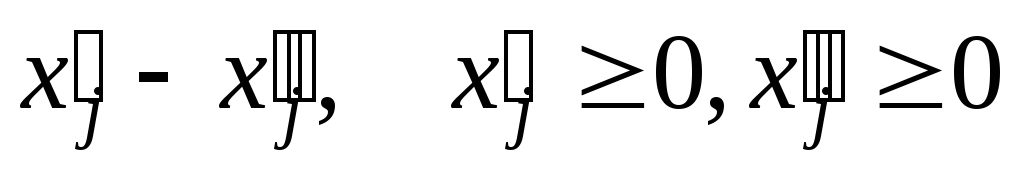– любую свободную переменную можно представить в виде разности двух неотрицательных переменных.

11. Графический анализ линейных моделей.

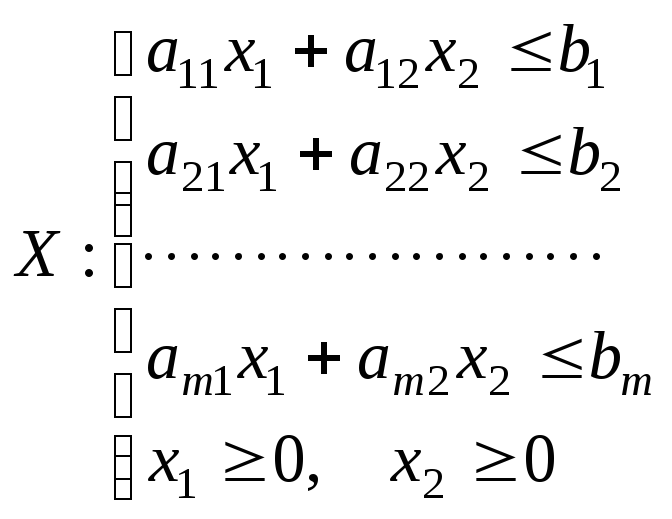
m = 3

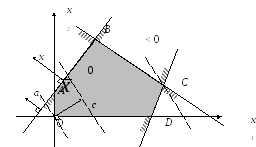
1. Строим границы множества решений, которые соответствуют неравенствам (прямые: )

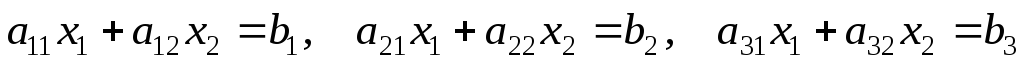2. Находим полуплоскости, соответствующие каждому ограничению (метод пробной точки)

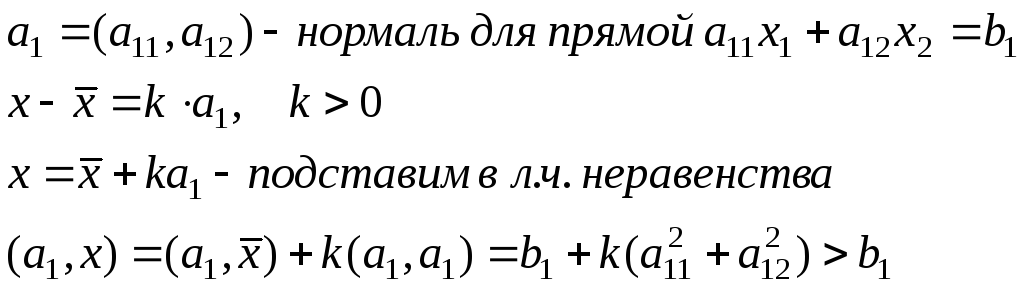
3. Находим многоугольник допустимых решений, как пересечение найденных полуплоскостей. Полученную область заштриховать. Возможные варианты:

   1. X– многоугольник

   2. X –пустое множество

   3. X –неограниченное многоугольное множество

4. Находим координаты вектора градиента целевой функции (вектор целей – вектор нормали к линиям уровня)

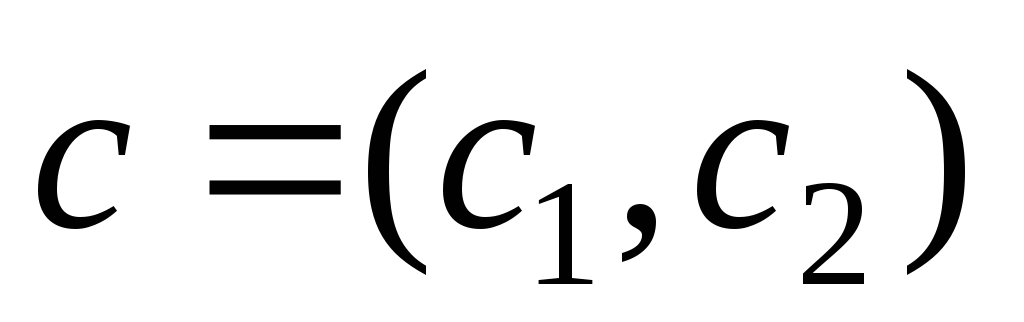
5. Строим прямую (перпендикулярно вектору цели), которая соответствует линии уровня для z₀= 0.

Затем перемещаем прямую в направлении вектора цели (в случае задачи на min– в противоположном направлении) до тех пор, пока прямая имеет общие точки с множеством допустимых решений. Крайнее положение – ответ.

6. Вычисляем координаты крайней точки, как пересечение соответствующих прямых и вычисляем значение целевой функции в этой точке.

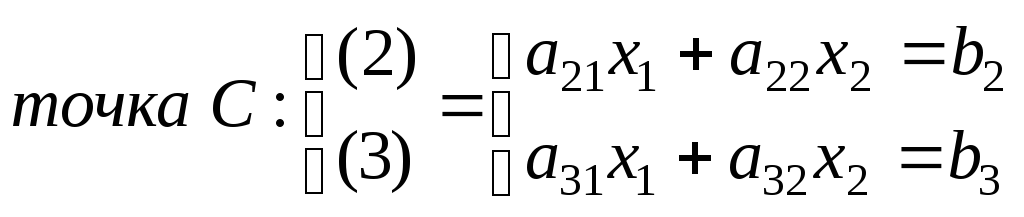
Ответ:

12. Двойственные модели ЛП, их экономическая интерпретация.

Рассмотрим задачу Lпланирования производства (1-ый вариант).

Скалярная форма	Матричная форма	Векторная форма

mресурсов.

b_i– объемi-го ресурсаnтехнологийа_ij– затратыi-го ресурса при использованииj-ой технологии в единицу времениc_j– получаемая ценность при использованииj-ой технологии в единицу времени

x_j– время работыj-ой технологии.

x= (x₁, …,x_n)

Оценим ценность затраченную и полученную в единицу времени

u_i– ценность единицыi-го ресурса

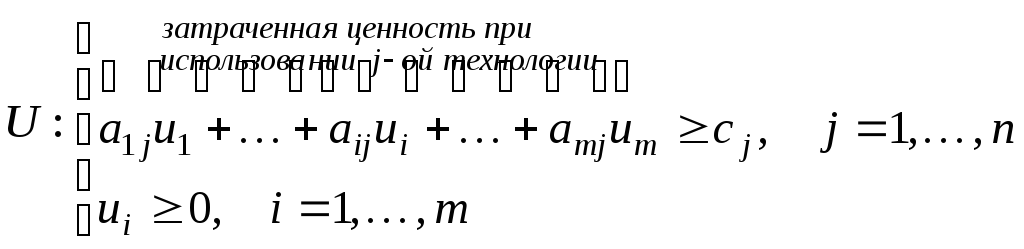
Скалярная форма	Матричная форма	Векторная форма

Δ – потери

x– план производства

L*– двойственная задача к задачеL

Скалярная форма	Матричная форма	Векторная форма

Двойственная задача возникает как задача минимизации потерь ценности в производстве, при условии, что само производство функционирует оптимальным образом, то есть в соответствии с оптимальным планом задачи L.

13. Правила построения двойственных моделей.

	L		L*
1.	Задача на max		Задача на min
2.	Матрица условий A		Матрица условий A^T
3.	m ограничений n переменных		n ограничений m переменных
4.	с– вектор цели b– вектор ограничений		b– вектор цели c– вектор ограничений
5.	Ограничение ≤		Ограничение ≥
6.	x ≥ 0		y ≥ 0