
- •Лекция 6. Непрерывность функции одной переменной
- •6. 1 Непрерывность функции в точке
- •6.2 Односторонняя непрерывность, связь с непрерывностью в точке
- •6.3 Классификация точек разрыва. Примеры
- •6.4 Свойства непрерывных функций
- •6.5 Арифметические операции над непрерывными функциями
- •6.6 Теорема о непрерывности сложной функции
- •6.7 Непрерывность элементарных функций
- •Лекция 7. Функции непрерывные на отрезке
- •7.1 Непрерывность функции на множестве
- •7.2 Первая теорема Вейерштрасса (об ограниченности функции, непрерывной на отрезке)
- •7.3 Вторая теорема Вейерштрасса (о достижении точных верхней и нижней граней непрерывной на отрезке функции)
- •7.3 Теоремы о корнях непрерывной функции теорема 3 (теорема Больцано-Коши о нуле непрерывной функции)
- •7.4 Обратная функция. Теорема о существовании и непрерывности обратной функции
- •7.5 Определение функции равномерно непрерывной на множестве. Теорема Кантора
- •Глава 3
- •§3.1 Производная функции
- •Бесконечные производные
6.4 Свойства непрерывных функций
ТЕОРЕМА 1 (о локальной ограниченности)
Если функция непрерывна в точке, то она ограничена в некоторой окрестности этой точки.
Пусть
![]() ,
,![]() .
.
ТЕОРЕМА 2 (об устойчивости знака непрерывной функции в точке)
Если функция
![]() непрерывна в точке
непрерывна в точке![]() и
и![]() ,
то
,
то![]()
![]() .
.
В самом деле, так
как
![]() непрерывна в точке
непрерывна в точке![]() ,
то
,
то![]() .
.
Тогда
![]()
![]() .
.
При этом
![]() ,
если
,
если![]() и
и![]() ,
если
,
если![]() .
.
Отсюда вытекает,
что, если функция
![]() непрерывна в точке
непрерывна в точке![]() и
и![]() ,
то она сохраняет знак в некоторой
окрестности точки
,
то она сохраняет знак в некоторой
окрестности точки![]() .
.
Следствие.
Пусть
![]() ,
,![]() ,
,![]() непрерывны в точке
непрерывны в точке![]() и
и![]() .
Тогда
.
Тогда![]() :
:![]()
![]() .
.
Доказательство.
Рассмотрим
![]()
![]() непрерывна в точке
непрерывна в точке![]() ,
,![]()
![]() :
:![]()
![]()
![]()
![]() .
.
6.5 Арифметические операции над непрерывными функциями
ТЕОРЕМА 3.
Сумма и произведение непрерывных функций
непрерывны: если функции
![]() :
:
![]() непрерывны в точке
непрерывны в точке
![]() ,
то функции
,
то функции![]() и
и![]() также непрерывны в этой точке.
также непрерывны в этой точке.
Доказательство.
Пусть
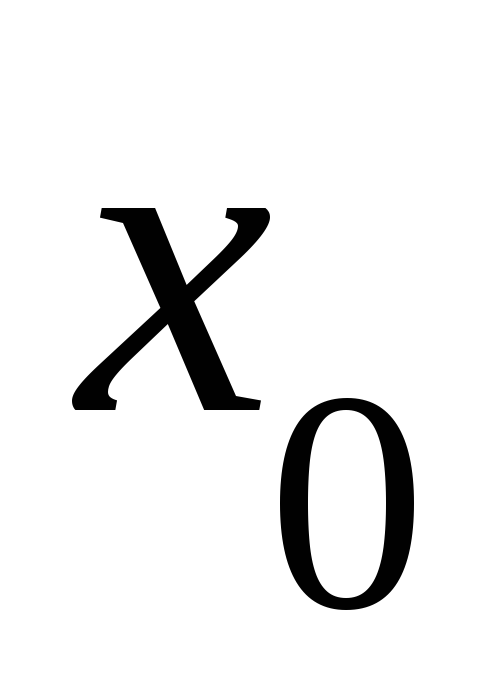 – изолированная точка. Тогда
– изолированная точка. Тогда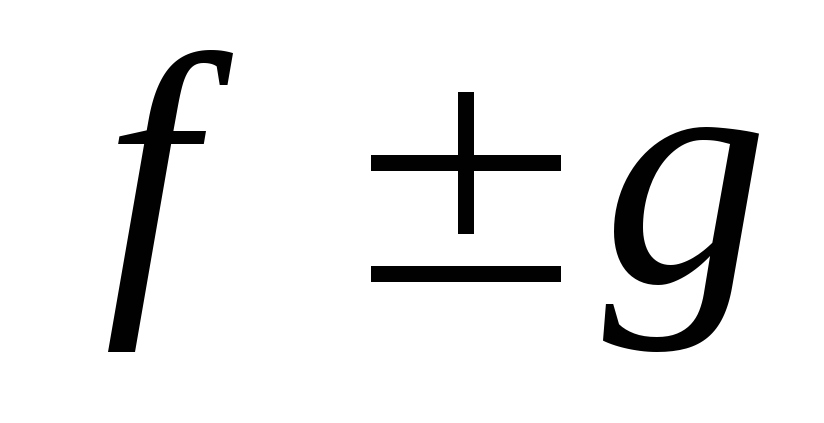 и
и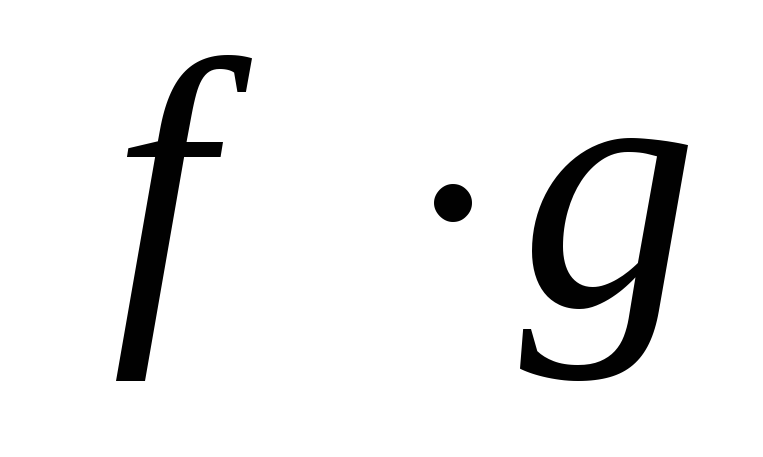 непрерывны по определению.
непрерывны по определению.Пусть
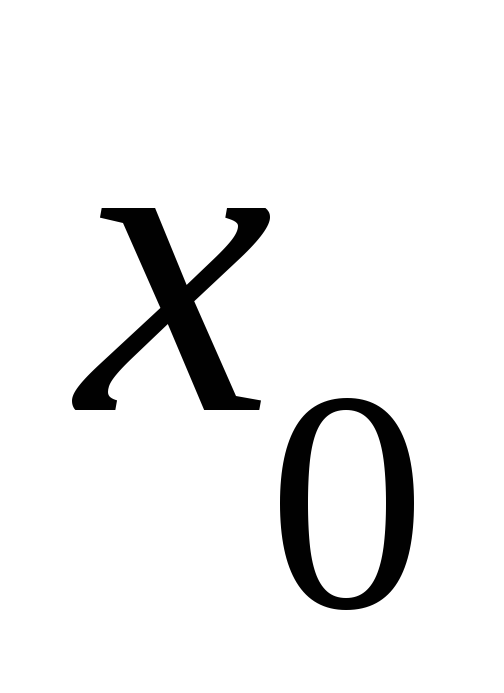 – предельная точка множестваХ.
Тогда
– предельная точка множестваХ.
Тогда
![]() ;
;
![]() .
.
ТЕОРЕМА 4.
Функция
![]() непрерывна в точке
непрерывна в точке![]() ,
если функция
,
если функция![]() непрерывна
в точке
непрерывна
в точке
![]() и
и![]() .
.![]()
![]()
Следствие.
Функция
![]() непрерывна в точке
непрерывна в точке![]() ,
если функции
,
если функции![]() непрерывны в точке
непрерывны в точке![]() и
и![]() .
.
6.6 Теорема о непрерывности сложной функции
ТЕОРЕМА 5
. Пусть
![]() ,
,![]() ,
функция
,
функция![]() непрерывна в точке
непрерывна в точке![]() ,
,![]() и функция
и функция![]() непрерывна в точке
непрерывна в точке![]() .
Тогда сложная функция
.
Тогда сложная функция![]() непрерывна в точке
непрерывна в точке![]() .
.
В самом деле,
![]() ,
(1)
,
(1)
![]() ,
,
но тогда согласно
теореме
о пределе композиции функций
![]() .
.
Из (1) вытекает, что
![]() .
Теорема доказана.
.
Теорема доказана.
Следствие.
Если
![]() ,
а
,
а![]() непрерывна в точке
непрерывна в точке![]() ,
то
,
то
![]() .
.
Итак, для непрерывной функции переход к пределу можно выполнять под знаком функции.
6.7 Непрерывность элементарных функций
Перечислим
основные
элементарные функции:
![]() (
(![]() ),
),
![]() (
(![]() ),
),
![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Определение. Функции, полученные из основных элементарных функций с помощью конечного числа арифметических операций и операций суперпозиции, называются элементарными.
Пример.
Функция
![]() является элементарной.
является элементарной.
Среди элементарных функций обычно выделяются:
целая рациональная функция или многочлен
![]() ,
,
здесь n
– степень многочлена,
![]() ;
;
![]() –коэффициенты
многочлена;
–коэффициенты
многочлена;
дробно-рациональная функция, являющаяся отношением двух многочленов
![]() .
.
Целые рациональные и дробно-рациональные функции образуют так называемый класс рациональных функций.
К элементарным функциям относят также те иррациональные функции, которые представляют суперпозицию рациональных функций и степенных функций с дробно-рациональными показателями.
Рациональные и иррациональные функции образуют класс алгебраических функций. Элементарные функции, которые не являются алгебраическими, называются трансцендентными функциями.
ПРИМЕР.
а)
![]() – целая рациональная функция,
– целая рациональная функция,
или многочлен четвёртой степени;
б)
![]() – дробно-рациональная функция;
– дробно-рациональная функция;
в)
![]() – иррациональная функция;
– иррациональная функция;
г)
![]() – трансцендентные функции.
– трансцендентные функции.
ТЕОРЕМА. Элементарные функции непрерывны в каждой точке своей области определения.
Доказательства вытекает из определения и теорем 3 - 5 (Свойства непрерывных функций).
Пример.
Покажем, что функция
![]() непрерывна
в любой точке
непрерывна
в любой точке
![]() .
.
Требуется доказать,
что
![]() .
.
Лемма.
![]()
![]() .
.
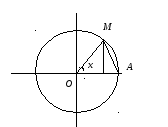
![]() ордината
точки
ордината
точки
![]() .
.
1. Пусть
![]() .
.
![]() ,
то есть
,
то есть
![]() ,
,
![]() .
.
2. Пусть
![]() .
.
![]() .
.
Итак,
![]() ,
,
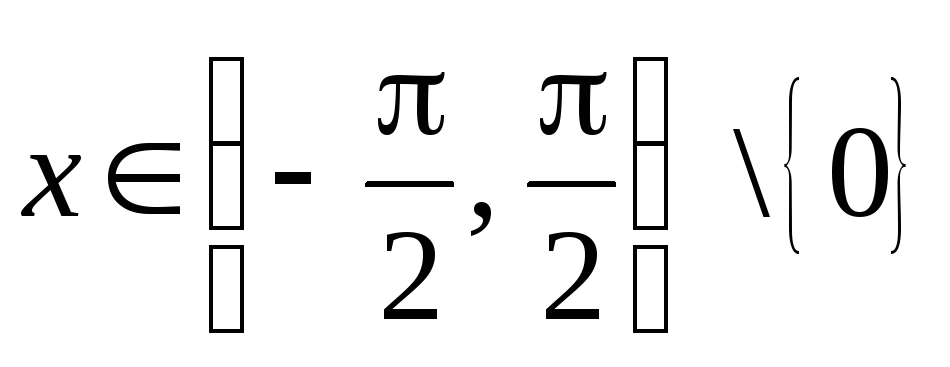 .
.
3. Ясно, что
![]() .
.
4. Пусть
![]() .
В этом случае
.
В этом случае
![]() .
Таким образом,
.
Таким образом,
![]()
![]() .
.
Лемма доказана.
Возьмем любое
положительное
![]() .
Оценим модуль разности
.
Оценим модуль разности![]()
![]() .
.
Пусть
![]() .
Тогда
.
Тогда
![]() .
Таким образом, функция
.
Таким образом, функция
![]() непрерывна в каждой точке
непрерывна в каждой точке
![]() .
.
Пример 2.
![]() ,
,
![]() .
Функция
.
Функция
![]() непрерывна и строго возрастает на
непрерывна и строго возрастает на
![]() .
Поэтому существует обратная функция,
которую обозначают
.
Поэтому существует обратная функция,
которую обозначают
![]() ,
определенная на
,
определенная на
![]() ,
возрастающая на
,
возрастающая на
![]() от
от![]() до
до![]() и непрерывная на этом отрезке.
и непрерывная на этом отрезке.
Пример 3.
![]() ,
,![]() ,
,![]() непрерывны на множестве
непрерывны на множестве![]() .
.
![]() непрерывна по
теореме 5.
непрерывна по
теореме 5.
В частности,
![]() ,
,![]() ,
непрерывна
,
непрерывна![]() .
.
Пример 4. Так как для непрерывной функции переход к пределу можно выполнять под знаком функции, то
![]()
![]() .
.
