
- •Лекция 6. Непрерывность функции одной переменной
- •6. 1 Непрерывность функции в точке
- •6.2 Односторонняя непрерывность, связь с непрерывностью в точке
- •6.3 Классификация точек разрыва. Примеры
- •6.4 Свойства непрерывных функций
- •6.5 Арифметические операции над непрерывными функциями
- •6.6 Теорема о непрерывности сложной функции
- •6.7 Непрерывность элементарных функций
- •Лекция 7. Функции непрерывные на отрезке
- •7.1 Непрерывность функции на множестве
- •7.2 Первая теорема Вейерштрасса (об ограниченности функции, непрерывной на отрезке)
- •7.3 Вторая теорема Вейерштрасса (о достижении точных верхней и нижней граней непрерывной на отрезке функции)
- •7.3 Теоремы о корнях непрерывной функции теорема 3 (теорема Больцано-Коши о нуле непрерывной функции)
- •7.4 Обратная функция. Теорема о существовании и непрерывности обратной функции
- •7.5 Определение функции равномерно непрерывной на множестве. Теорема Кантора
- •Глава 3
- •§3.1 Производная функции
- •Бесконечные производные
7.3 Теоремы о корнях непрерывной функции теорема 3 (теорема Больцано-Коши о нуле непрерывной функции)
Пусть
![]() и
и![]() .
Тогда
.
Тогда![]() такое, что
такое, что![]() .
.
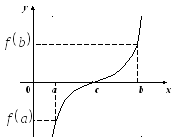
Доказательство.
Пусть
![]() ,
,![]() .
Разделим отрезок
.
Разделим отрезок![]() пополам:
пополам:
если
 ,
то
,
то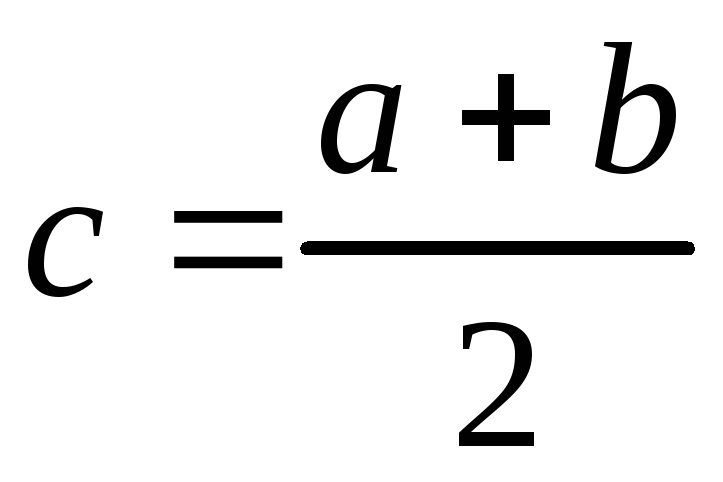 ;
;если
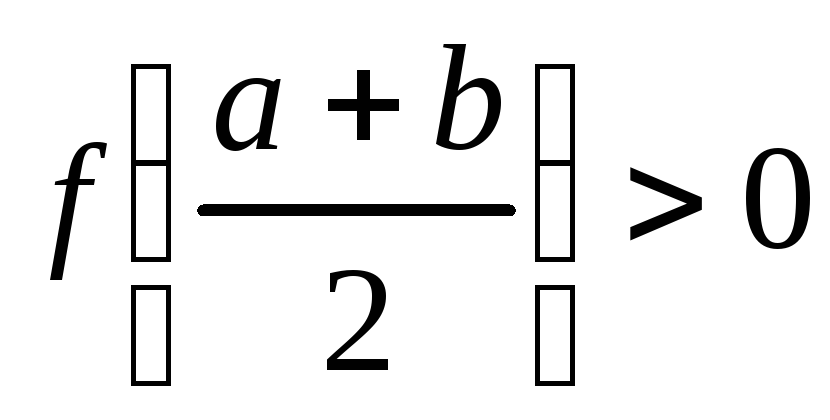 ,
то обозначим
,
то обозначим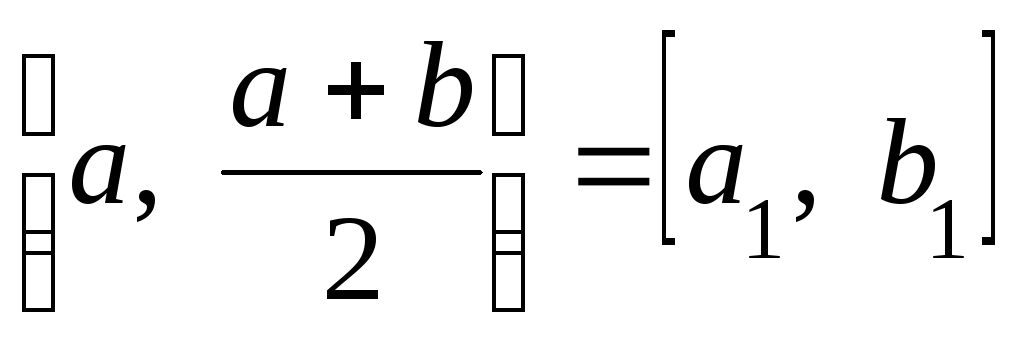 ,
,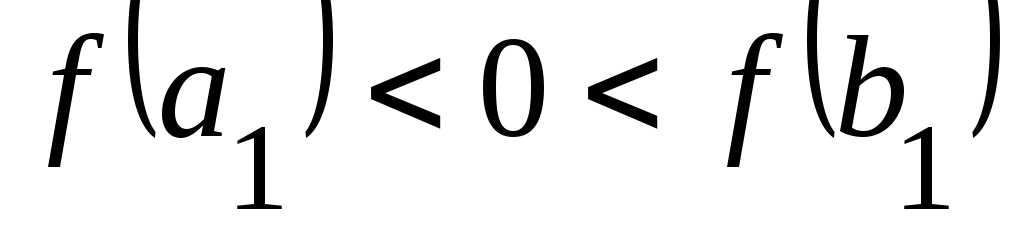 ;
;если
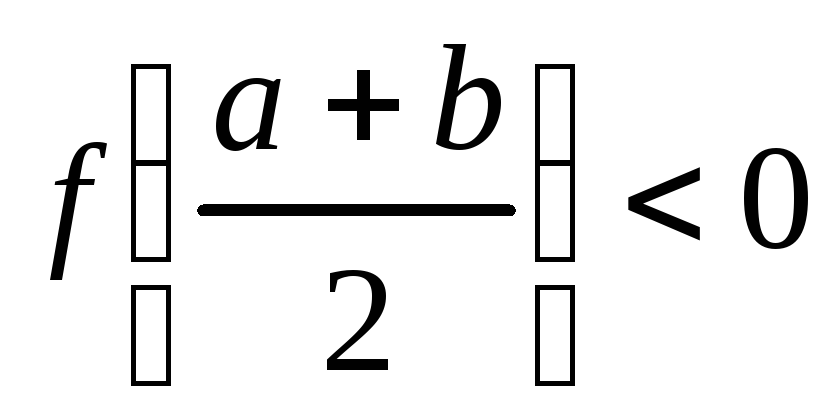 ,
то обозначим
,
то обозначим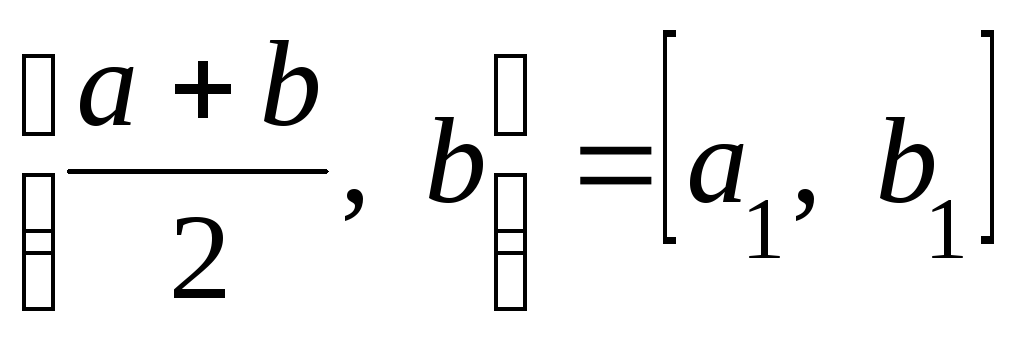 ,
,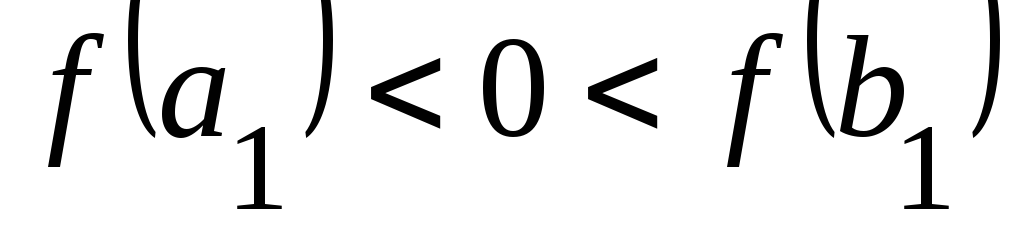 .
.
Заметим,
что длина отрезка
![]() в два раза меньше длины отрезка
в два раза меньше длины отрезка![]() .
.
Разделим
теперь отрезок
![]() пополам и повторим предыдущие рассуждения.
То есть, если в точке деления функция
обращается в ноль, то нужная точка уже
найдена. В противном случае выберем тот
из получившихся отрезков, в концах
которого функция принимает значения
разных знаков. Обозначим этот отрезок
пополам и повторим предыдущие рассуждения.
То есть, если в точке деления функция
обращается в ноль, то нужная точка уже
найдена. В противном случае выберем тот
из получившихся отрезков, в концах
которого функция принимает значения
разных знаков. Обозначим этот отрезок![]() и заметим, что
и заметим, что![]() и
и![]() .
.
Продолжим
этот процесс. Если
![]() ,
то
,
то![]() .
.
Если мы
не встретим нуль функции на каком-то
шаге, то получим последовательность
вложенных отрезков
![]() ,
длины которых
,
длины которых![]() .
Значит, согласнолемме
Коши-Кантора о вложенных
отрезках существует точка
.
Значит, согласнолемме
Коши-Кантора о вложенных
отрезках существует точка
![]() .
.
Докажем,
что
![]() .
Так как последовательность
.
Так как последовательность![]() и ограничена,
и ограничена,![]() .
Так как последовательность
.
Так как последовательность![]() и ограничена,
и ограничена,![]() .
Для каждого
.
Для каждого![]()
![]() ,
следовательно,
,
следовательно,![]() .
.
Функция
![]() непрерывна в точке
непрерывна в точке![]() ,
поэтому
,
поэтому
![]() ,
,
![]() .
.
![]() ,
(1)
,
(1)
![]() .(2)
.(2)
Из (1) и (2) вытекает,
что![]() .Теорема доказана.
.Теорема доказана.
Следствие (теорема о прохождении непрерывной на отрезке функции через любое промежуточное значение).
Пусть
![]() и
и![]() .
Тогда для любого числа
.
Тогда для любого числа![]() ,
заключенного между
,
заключенного между![]() и
и![]() ,
существует такое
,
существует такое![]() ,
что
,
что
![]() .
.

Доказательство.
Рассмотрим функцию
![]() .
Функция
.
Функция![]() непрерывна на
непрерывна на![]() и
и![]() .
Согласно теореме Больцано-Коши о нуле
непрерывной функции
.
Согласно теореме Больцано-Коши о нуле
непрерывной функции![]() ,
то есть
,
то есть![]() .
Теорема доказана.
.
Теорема доказана.
Следствие.
Если функция ![]() непрерывна на
непрерывна на
![]() ,
то
,
то
![]() ,
(3)
,
(3)
где
![]() ,
,![]() .
.
Доказательство.
Для каждого
![]()
![]() ,
поэтому
,
поэтому
![]() .
(4) По теореме Вейерштрасса
.
(4) По теореме Вейерштрасса![]() ,
,![]() .
.
Пусть
![]() (если
(если![]() ).
Имеем
).
Имеем![]() :
:![]() ,
,![]() .
По теореме Больцано-Коши о промежуточных
значениях
.
По теореме Больцано-Коши о промежуточных
значениях![]()
![]() .
То есть мы доказали, что функция
.
То есть мы доказали, что функция![]() принимает все
значения от
принимает все
значения от
![]() до
до![]() ,
следовательно,
,
следовательно,
![]() .
(5)
.
(5)
Из (4) и (5) вытекает (3).
Другая формулировка следствия:
Если
![]() ,
то
,
то![]() .
.
7.4 Обратная функция. Теорема о существовании и непрерывности обратной функции
Лемма.
Функция
![]() ,
монотонная на
,
монотонная на![]() ,
непрерывна на нем тогда только тогда,
когда,
,
непрерывна на нем тогда только тогда,
когда,![]() .
.
Доказательство.
Необходимость. Согласно следствию из
теоремы Больцано-Коши о промежуточных
значениях
![]() .
.
Пусть функция
![]() возрастает на
возрастает на![]() .
Тогда
.
Тогда![]()
![]() ,
следовательно,
,
следовательно,![]() ,
,![]() .
.
Достаточность.
Пусть функция
![]() монотонно возрастает на
монотонно возрастает на![]() и
и![]() .
Покажем, что функция
.
Покажем, что функция![]() непрерывна на
непрерывна на![]() .
Доказательство проведем от противного.
Предположим, что функция
.
Доказательство проведем от противного.
Предположим, что функция![]() разрывна и пусть
разрывна и пусть![]() - точка разрыва (первого рода!). Возможны
три случая:
- точка разрыва (первого рода!). Возможны
три случая:
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
1) Если
![]() ,
то, так как функция
,
то, так как функция![]() возрастает, то
возрастает, то![]() ,
,![]() ,
,![]() ,
причем
,
причем![]() (в силу монотонности функции)
(в силу монотонности функции)

Выберем такое
число
![]() ,
что
,
что
![]() (6)
(6)
Так как
![]() ,
,![]() ,
то
,
то![]() .
Если
.
Если![]() ,
то
,
то![]() ,
что противоречит (6).
,
что противоречит (6).
Так как
![]() ,
то
,
то![]()
![]() .
Поэтому, если
.
Поэтому, если![]() ,
то
,
то![]() ,
то есть
,
то есть![]() ,
что опять противоречит выбору
,
что опять противоречит выбору![]() .
Таким образом, точка
.
Таким образом, точка![]() не может быть точкой разрыва функции
не может быть точкой разрыва функции![]() .
.
2) Доказывается аналогично.
3)
![]() .
Пусть
.
Пусть![]() ,
,![]() .
.
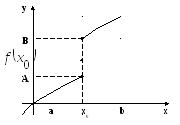

![]()
![]() Так как
Так как
![]() ,
то
,
то
![]() ,
(7)
,
(7)
а так как
![]() – точка разрыва (первого рода), то
– точка разрыва (первого рода), то![]() (одно из неравенств в (7) является
строгим).
(одно из неравенств в (7) является
строгим).
Выберем
![]() (
(![]() )
так, что
)
так, что![]() .
(8) Так как
.
(8) Так как![]() ,
то
,
то![]() .
Имеем
.
Имеем![]() .
Поэтому
.
Поэтому![]()
![]() .
Если
.
Если![]() ,
то
,
то![]() ,
что противоречит (8). Так как
,
что противоречит (8). Так как![]() ,
то
,
то![]()
![]() .
Если
.
Если![]() ,
то
,
то![]() ,
что противоречит (8).
,
что противоречит (8).
Если
![]() ,
то
,
то![]() ,
что также противоречит выбору числа
,
что также противоречит выбору числа![]() .
.
Таким образом,
точка
![]() не может быть точкой разрыва функции.
не может быть точкой разрыва функции.
Лемма доказана.
Пусть
![]() биективное отображение. В таком случае
функция
биективное отображение. В таком случае
функция![]() обратима. Справедлива
обратима. Справедлива
Теорема о существовании и непрерывности обратной функции
ТЕОРЕМА.
Пусть функция
![]() строго возрастает (убывает) и непрерывна
на
строго возрастает (убывает) и непрерывна
на![]() .
Тогда:
.
Тогда:
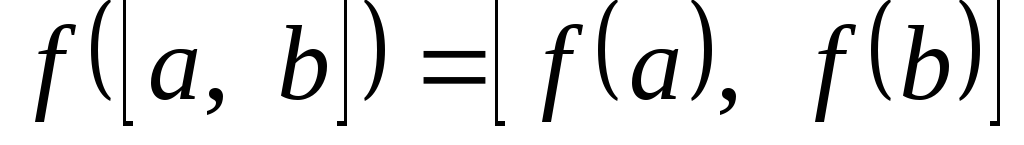 ;
; обратима;
обратима;
C)
обратная функция
![]() непрерывна и строго возрастает (убывает)
на
непрерывна и строго возрастает (убывает)
на![]() .
.
Доказательство.
А) Смотри лемму.
B)
Отображение
![]() биективно (
биективно (![]() или
или
![]() )
и, значит, обратимо.(Смотри
Обратное отображение (Лекция №4)).
)
и, значит, обратимо.(Смотри
Обратное отображение (Лекция №4)).
С) Пусть
![]() строго возрастает на
строго возрастает на![]() .
Покажем, что
.
Покажем, что![]() строго возрастает на
строго возрастает на![]() .
Пусть
.
Пусть![]() ,
,![]() .
Тогда
.
Тогда![]() ,
,![]() .
Для
.
Для![]() .
В самом деле, если
.
В самом деле, если![]() ,
то есть
,
то есть![]() ;
если
;
если![]() ,
то есть
,
то есть![]() .
Поэтому
.
Поэтому![]() .
.![]()
Так как
![]() строго возрастает на
строго возрастает на![]() и
и![]() ,
то по лемме
,
то по лемме![]() непрерывна на
непрерывна на![]() .
Теорема доказана.
.
Теорема доказана.
