7.5 Определение функции равномерно непрерывной на множестве. Теорема Кантора

Пусть функция непрерывна на множестве (промежутке) . Это значит, что для любой точкии.

Здесь зависит и от иот .

Понятие равномерной непрерывности – это более сильное ограничение на функцию.

Определение. Функция называетсяравномерно непрерывной на множестве, если для любого

.

Здесь зависит только от .

Таким образом, для равномерно непрерывной функции значения функции близки, как только близки значения аргументов, где бы они не находились.

Если функция равномерно непрерывна на промежутке X, то она также является непрерывной на нем. Обратное неверно, как видно из следующих примеров.

Пример. Покажем, что функция не является равномерно непрерывной.

Для функции на всей числовой прямой . Значит, зависит и оти от. Поэтому функция не является равномерно непрерывной.

Пример. Покажем, что функция не является равномерно непрерывной на множестве.

Заметим, что 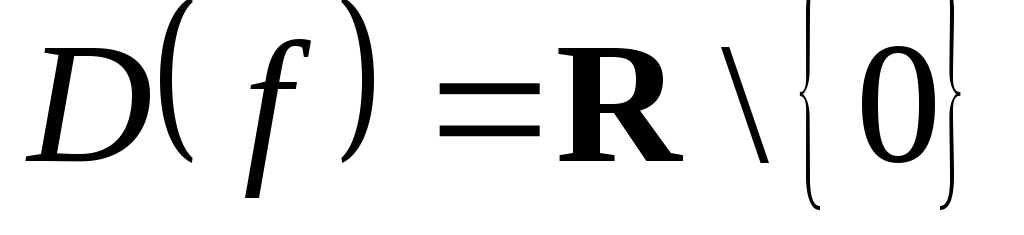_. Точка является предельной для_.

Рассмотрим две последовательности:

, для нее ,

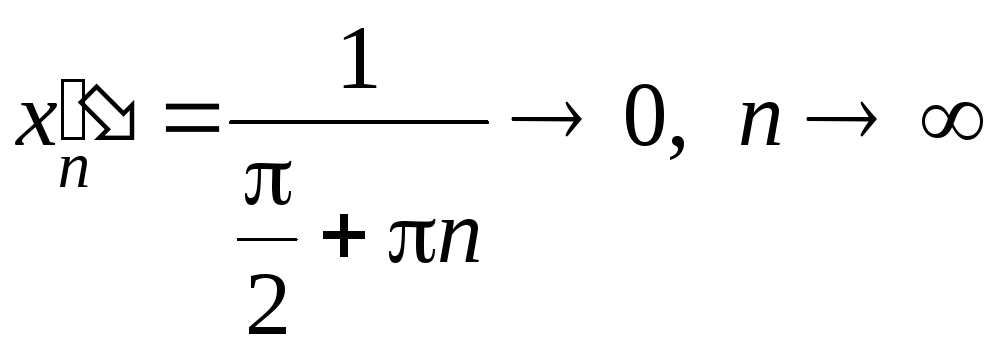, для нее .

Тогда ,. Таким образом,

для нельзя найти единогодля всех точек из.

Однако, если функция непрерывна на отрезке, то ситуация меняется.

ТЕОРЕМА Кантора. Если функция непрерывна на отрезке, то она равномерно непрерывна на этом отрезке.

Доказательство. Предположим противное. Пусть функция не является равномерно непрерывной на. Тогда

.

При каждом возьмем. Тогда

. По теореме Больцано-Вейерштрасса из ограниченной последовательности можно выделить сходящуюся к некоторой точке подпоследовательность.

Чтобы не усложнять обозначений, будем считать, что уже сама последовательность . Тогда, т. к.. Поскольку функция непрерывна в точке, то. Тогда. Отсюда, а это противоречит тому, что. Значит, предположение неверно, и функция равномерно непрерывна на отрезке.

Глава 3

Дифференциальное исчисление

§3.1 Производная функции

Пусть определена на множестве и - предельная точка множества . Для любой точки приращение определяется формулой . Приращением функции в точке называется функция аргумента .

.

Определение. Если существует предел

, (3.1.1)

то значение этого предела называют производной функции в точке , обозначают и говорят, что функция имеет в точке производную.

Используются и другие символические обозначения производной:

, , .

Лагранж Ньютон Лейбниц

(1736-1813) (1642-1727) (1646-1716)

Так как , то и приращение функции в точке имеет вид .

Определение производной можно записать также в виде формулы

, (3.1.2)

если предел (3.1.2) существует.

Физический смысл производной

Производная - скорость изменения функции в точке . В частности, если - время,- координата точки, движущейся по прямой в момент, то - мгновенная скорость точки в момент времени .

Геометрический смысл производной

Пусть график функции ; ,- две точки на

Угол между секущей и осьюобозначим.

Определение. Если , то прямаяс угловым коэффициентом, проходящая через точку, называется касательной к графику функциив точке .

Теорема. График функции имеет в точкекасательную тогда и только тогда, когда функцияимеет в точке производную .

Доказательство. Необходимость. Пусть , так как функциянепрерывна, то. Но. Поэтому, то есть функцияимеет в точкеконечную производную .

Достаточность. Если существует , то есть , то, но так как функции,непрерывные, то, то есть существует касательная к графику функции в точке.

Замечание. Так как , то приполучаем, то есть - это тангенс угла наклона касательной к графику функции в точке .

Найдем уравнение касательной. Будем искать его в виде . Так как, то, откуда. Поскольку угловой коэффициент касательной , то ее уравнение имеет вид .