- •Лекция 6. Непрерывность функции одной переменной
- •6. 1 Непрерывность функции в точке
- •6.2 Односторонняя непрерывность, связь с непрерывностью в точке
- •6.3 Классификация точек разрыва. Примеры
- •6.4 Свойства непрерывных функций
- •6.5 Арифметические операции над непрерывными функциями
- •6.6 Теорема о непрерывности сложной функции
- •6.7 Непрерывность элементарных функций
- •Лекция 7. Функции непрерывные на отрезке
- •7.1 Непрерывность функции на множестве
- •7.2 Первая теорема Вейерштрасса (об ограниченности функции, непрерывной на отрезке)
- •7.3 Вторая теорема Вейерштрасса (о достижении точных верхней и нижней граней непрерывной на отрезке функции)
- •7.3 Теоремы о корнях непрерывной функции теорема 3 (теорема Больцано-Коши о нуле непрерывной функции)
- •7.4 Обратная функция. Теорема о существовании и непрерывности обратной функции
- •7.5 Определение функции равномерно непрерывной на множестве. Теорема Кантора
- •Глава 3
- •§3.1 Производная функции
- •Бесконечные производные
Бесконечные производные
Если функция
![]() непрерывна в точке
непрерывна в точке
![]() и
и![]() равен
равен![]() или
или![]() ,
то говорят, что функция
,
то говорят, что функция![]() имеет в точке
имеет в точке
![]() бесконечную производную (равную
бесконечную производную (равную![]() или
или![]() соответственно). В этом случае касательная
к графику функции в точке
соответственно). В этом случае касательная
к графику функции в точке![]() параллельна оси
параллельна оси![]() (
(![]() ),
и ее уравнение
),
и ее уравнение![]() (так
как она проходит через точку
(так
как она проходит через точку![]() ).
).
Пример 10.
![]() ,
,![]() .
.
![]()
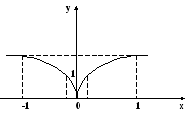 - вертикальная
касательная к графику
- вертикальная
касательная к графику
 функции.
функции.
Пример
20.
![]() ,
,![]() .
.
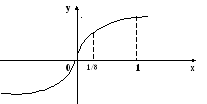
![]() -
вертикальная касательная.
-
вертикальная касательная.
Односторонние производные
Пусть
![]() определена на множестве
определена на множестве![]() и
и![]() - предельная точка
- предельная точка![]() (
(![]() ).
Если
).
Если![]() (
(![]() ),
то его называют левой производной
функции
),
то его называют левой производной
функции![]() в точке
в точке
![]() и обозначают
и обозначают![]() .
.![]()
Аналогично
![]() .
.
Число
![]() (если оно существует), называется правой
производной функции
(если оно существует), называется правой
производной функции![]() в точке
в точке
![]() .
.
Теорема.
Пусть
![]() - предельная точка
- предельная точка![]() .
Функция
.
Функция![]() имеет производную в точке
имеет производную в точке![]()
![]()
![]() ,
,![]() ,
причем
,
причем![]() .
.
Пример.
![]() .
.![]() .
Так как
.
Так как
![]()
![]() ,
то
,
то
![]() не существует.
не существует.
Пример.
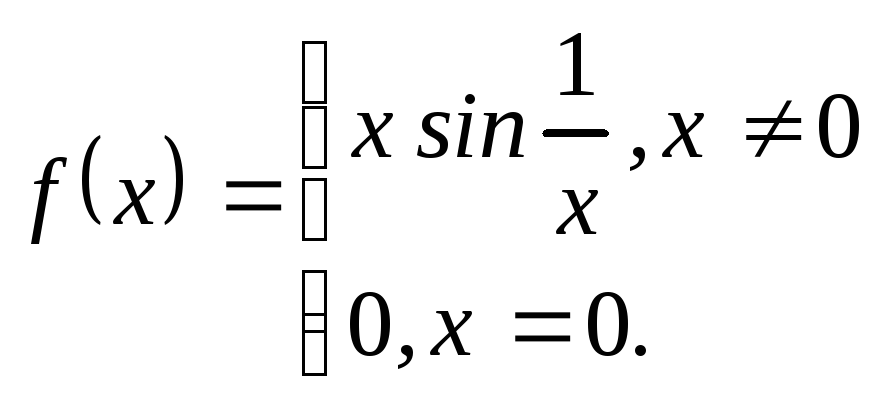
![]() ,
то есть
,
то есть
![]() непрерывна в точке
непрерывна в точке![]() .
.
 не
существует, так как
не
существует, так как
![]()
![]() .
(предел по Гейне не существует).
.
(предел по Гейне не существует).
Дифференцируемость функции в точке
Определение.
Функция
![]() ,
определенная на множестве
,
определенная на множестве![]() ,
называется дифференцируемой в точке
,
называется дифференцируемой в точке![]() ,
предельной для множества
,
предельной для множества![]() ,
если существует такая линейная
относительно приращениям
,
если существует такая линейная
относительно приращениям![]() функция
функция![]() (
(![]() - некоторое число), что приращение
- некоторое число), что приращение![]() функции
функции![]() представляется в виде
представляется в виде![]() (1), где
(1), где![]() .
.
Так как
![]() ,
то (1) можно записать в виде
,
то (1) можно записать в виде![]() (1). Геометрически (1) означает, что
(1). Геометрически (1) означает, что![]() ,
то есть в достаточно малой окрестности
точки
,
то есть в достаточно малой окрестности
точки![]() график функции
график функции![]() сливается с некоторой невертикальной
прямой, то есть “спрямляется”.
сливается с некоторой невертикальной
прямой, то есть “спрямляется”.
Теорема.
Для того чтобы функция
![]() была дифференцируемой в точке
была дифференцируемой в точке![]() ,
необходимо и достаточно, чтобы она имела
в этой точке конечную производную.
,
необходимо и достаточно, чтобы она имела
в этой точке конечную производную.
Доказательство.
Необходимость. Пусть функция
![]() дифференцируема в точке
дифференцируема в точке![]() .
Тогда ее приращение можно представить
в виде (1). Имеем
.
Тогда ее приращение можно представить
в виде (1). Имеем
![]() .
.
Следовательно,
производная
![]() существует и
существует и![]() .
.
Достаточность.
Пусть конечная производная
![]() .
Тогда по определению производной
.
Тогда по определению производной![]() .
.
Положим
![]()
![]() (2), если
(2), если![]() .
Функция
.
Функция![]() является бесконечно малой при
является бесконечно малой при![]() .
Действительно,
.
Действительно,![]() .
.
Кроме
того, из (2)
![]() ,
тем самым доказано, что функция
,
тем самым доказано, что функция![]() дифференцируема в точке
дифференцируема в точке![]() .
.
Теорема.
Если функция
![]() дифференцируема в точке
дифференцируема в точке![]() ,
то она непрерывна в этой точке.
,
то она непрерывна в этой точке.
Доказательство.
Из (1) вытекает
![]() ,
то есть функция
,
то есть функция![]() непрерывна в точке
непрерывна в точке![]() .
.
Обратное
утверждение неверно. Функция
![]() непрерывна в каждой точке. С другой
стороны, в точке
непрерывна в каждой точке. С другой
стороны, в точке![]() функция
функция![]() не имеет производной и по доказанной
теореме не является дифференцируемой.
не имеет производной и по доказанной
теореме не является дифференцируемой.
Дифференциал и приближенное вычисление
Определение.
Дифференциалом функции
![]() в точке
в точке![]() (дифференцируемой в этой точке) называется
линейная функция приращения
(дифференцируемой в этой точке) называется
линейная функция приращения![]() :
:
![]() .
.
Формулу
(1) приращения дифференцируемой функции
можно записать так:
![]() .
.
Разность
![]() имеет более высокий порядок малости по
сравнению с
имеет более высокий порядок малости по
сравнению с![]() ,
по этой причине говорят, что дифференциал
есть главная (линейная относительно
,
по этой причине говорят, что дифференциал
есть главная (линейная относительно![]() )
часть приращения функции
)
часть приращения функции![]()
![]() в
точке
в
точке![]() .
.
Если
![]() ,
то, очевидно,
,
то, очевидно,![]() и
и![]() ,
то есть
,
то есть![]() .
.
Поэтому
![]() (1)
(1)
или
![]() ,
,
то
есть отношение дифференциалов
![]() и
и![]() равно
равно![]() .
По этой причине, следуя Лейбницу,
производную часто обозначают символом
.
По этой причине, следуя Лейбницу,
производную часто обозначают символом![]() наряду с предложенным впоследствии
Лагранжем символом
наряду с предложенным впоследствии
Лагранжем символом![]() .
.
Ж.Л. Лагранж (1736-1813) – знаменитый французский математик и механик.
Если
![]() ,
то
,
то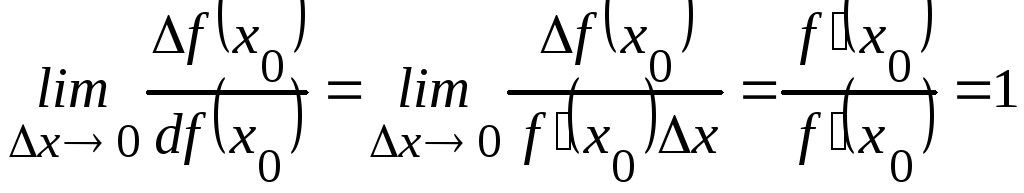 ,
то есть
,
то есть![]() ,
,![]() .
(2)
.
(2)
Этим
часто пользуются для приближенного
вычисления значений дифференцируемой
функции из некоторой
![]() - окрестности точки
- окрестности точки![]() при достаточно малом
при достаточно малом![]() .
Для этого формулу (2) записывают в виде
.
Для этого формулу (2) записывают в виде![]() (3) или
(3) или![]() (4).
(4).
Замечание.
Соотношением (4) функция
![]() линеаризована в окрестности точки
линеаризована в окрестности точки![]() .
.


Функция
дифференцируема в точке x0 Существует
конечная производная
![]()

Функция
непрерывна в точке x0