
- •Федеральное агентство по образованию
- •Часть 1. Неопределённый интеграл
- •На будущее:
- •Наиболее популярные методы решения неопределённых интегралов
- •1. Замена переменной интегрирования.
- •2. Приведение к «табличному виду»
- •3. Замена функции
- •4. Интегрирование «по частям»
- •Рациональные дроби
- •Метод «неопределённых коэффициентов»
- •6. Тригонометрические функции
- •6.1. Интегралы типа ,
- •6.2. Интегралы типа
- •6.3. Интегралы типа
- •8. Интегралы с иррациональностью типа
- •Приложение 2 Построение таблицы исходных данных и соответствующего ей совмещённого графика
- •Построение графика
- •Часть I. Неопределённый интеграл
4. Интегрирование «по частям»
Идея этого метода
основана на формуле производной
произведения двух функций:
![]() [1] ─ применяется чаще всего тогда, когда
подынтегральная функция может быть
представлена в виде произведения пары
хотя бы одной из следующих функций:
[1] ─ применяется чаще всего тогда, когда
подынтегральная функция может быть
представлена в виде произведения пары
хотя бы одной из следующих функций:![]()
![]() и их вариаций.
и их вариаций.
Итак, если
подынтегральную функцию
![]() можно представить в виде произведения
можно представить в виде произведения![]() ,
то сочетание
,
то сочетание![]() или
или![]() можно принять за дифференциал
можно принять за дифференциал![]() или
или![]() .
Тогда решение интеграла получается по
формуле
.
Тогда решение интеграла получается по
формуле![]()
![]() .
.
Выбор функций-сомножителей определяется опытом самого решающего. Попытаемся показать это на конкретном примере.
Пример
7.
![]() .
.
Рецепт.
Альтернатива выбора функций-сомножителей
здесь небогатая: либо
![]() и
и![]() ,
либо
,
либо![]() .
Попробуем пойти первым путём
.
Попробуем пойти первым путём
Вариант 1.
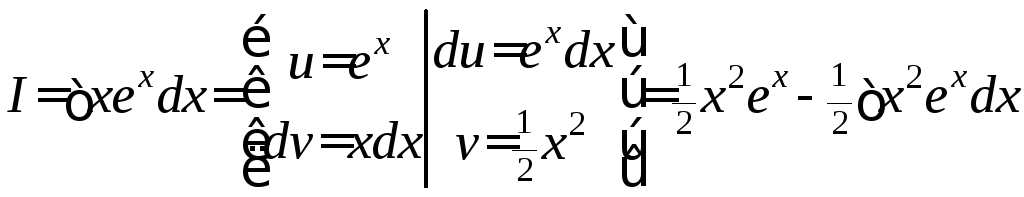 .
Повторно применяем этот же метод:
.
Повторно применяем этот же метод: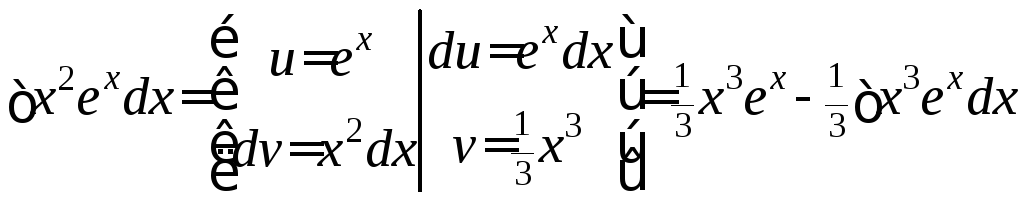 и т.д. Очевидно, что этот путь ─тупиковый:
с каждым
новым шагом показатель степени при
аргументе растёт
и не видно конца этим манипуляциям.
Очевидна и причина такого тупика ─
неудачный первоначальный выбор функции
и т.д. Очевидно, что этот путь ─тупиковый:
с каждым
новым шагом показатель степени при
аргументе растёт
и не видно конца этим манипуляциям.
Очевидна и причина такого тупика ─
неудачный первоначальный выбор функции
![]() .
.
Не следует думать, что есть люди, которые ни разу не совершали подобную ошибку, просто из этого надо сделать позитивный вывод: «на ошибках учатся».
А теперь пойдём альтернативным путём:
Вариант 2:
![]() .
Тогда
.
Тогда
![]() .
.
Интересной особенностью данного метода является решение «рекурсивных интегралов». Рассмотрим один из вариантов таких интегралов.
Пример
8.
![]() .
.
Рецепт.
Применим метод «по частям»:
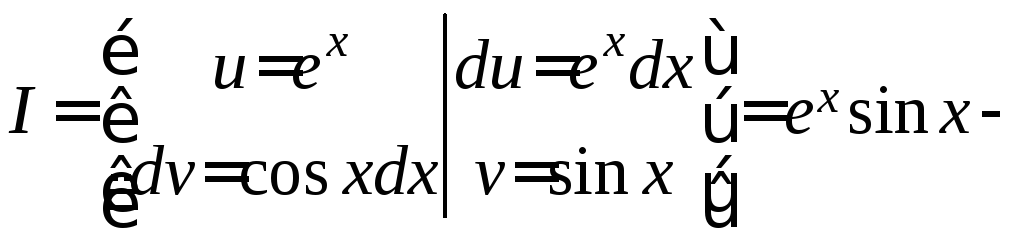
![]()
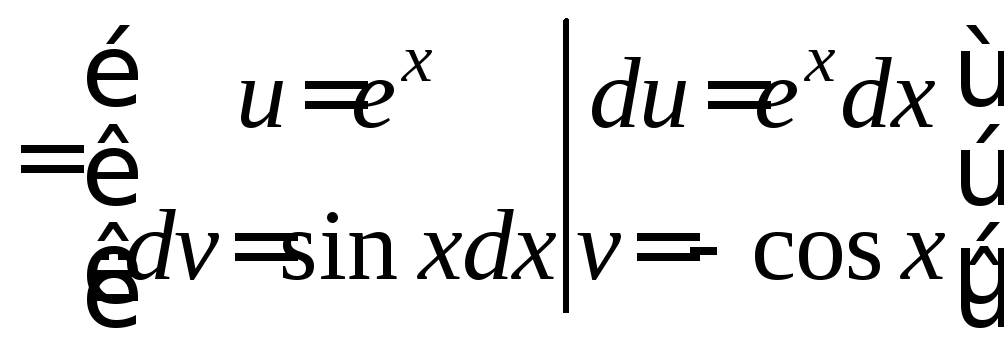
![]()
![]() .
.
Сопоставив начало
и конец этой цепочки, получаем решение
![]() .
.
Рациональные дроби
Известно [1], что
дробь может называться «рациональной»,
если её числитель и знаменатель ─ целые
числа. С этой точки зрения излагаемый
дальше метод относится к интегралам
вида
![]() ,
где
,
где![]()
![]() ,
а
,
а![]() ─ полиномы порядка
─ полиномы порядка![]() и
и![]() соответственно.
соответственно.
С точки зрения соотношения порядков полиномов возможны два варианта:
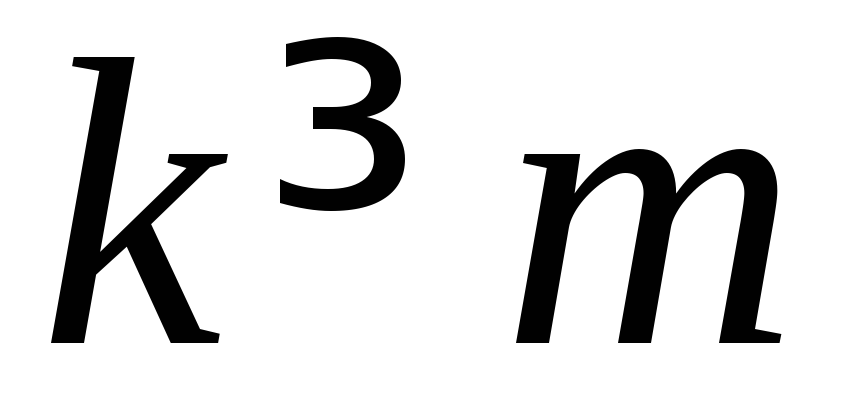 .
В этом случае полином числителя
«столбиком» делят на полином знаменателя,
выделяя тем самым «целую» часть
подынтегральной дроби и её «остаток».
Тогда исходный интеграл можно представить
в виде суммы двух интегралов:
.
В этом случае полином числителя
«столбиком» делят на полином знаменателя,
выделяя тем самым «целую» часть
подынтегральной дроби и её «остаток».
Тогда исходный интеграл можно представить
в виде суммы двух интегралов:
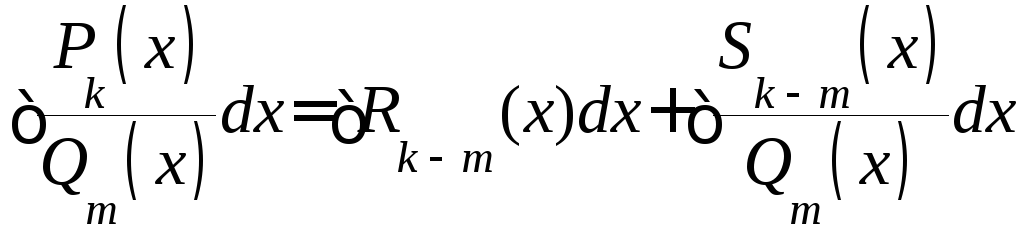 ,
где
,
где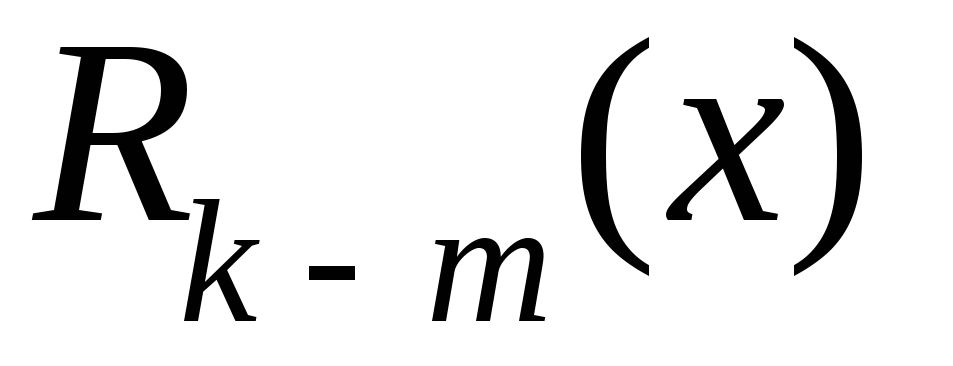
и
![]() ─
полиномы соответствующего порядка того
же типа, что и исходные полиномы. Первый
интеграл – сумма табличных интегралов.
Ко второму интегралу применяют обычно
метод «неопределённых коэффициентов»,
суть которого излагается дальше;
─
полиномы соответствующего порядка того
же типа, что и исходные полиномы. Первый
интеграл – сумма табличных интегралов.
Ко второму интегралу применяют обычно
метод «неопределённых коэффициентов»,
суть которого излагается дальше;
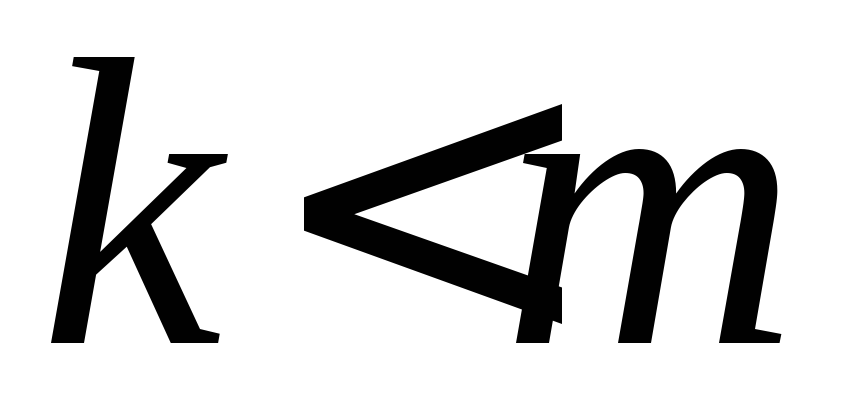 .
Здесь сразу берётся интеграл указанным
выше методом.
.
Здесь сразу берётся интеграл указанным
выше методом.
Метод «неопределённых коэффициентов»
Известно [1], что
любой полином
![]() го
порядка (n≥2)
можно представить в виде произведения:
го
порядка (n≥2)
можно представить в виде произведения:
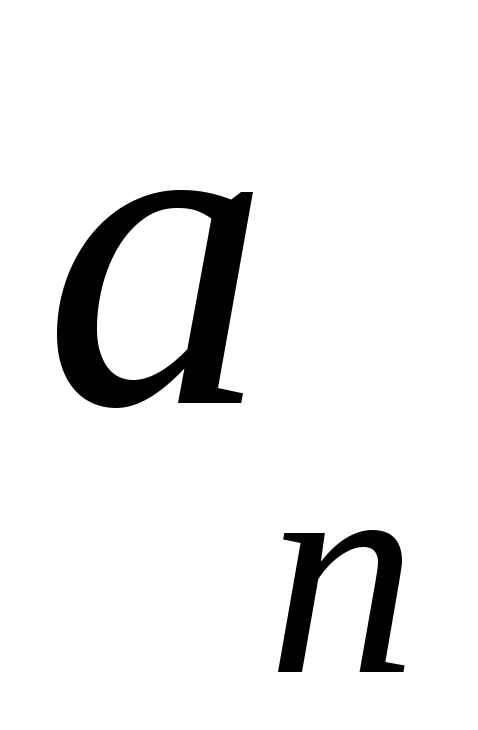 (коэффициента при
старшей степени полинома);
(коэффициента при
старшей степени полинома);двучленов типа
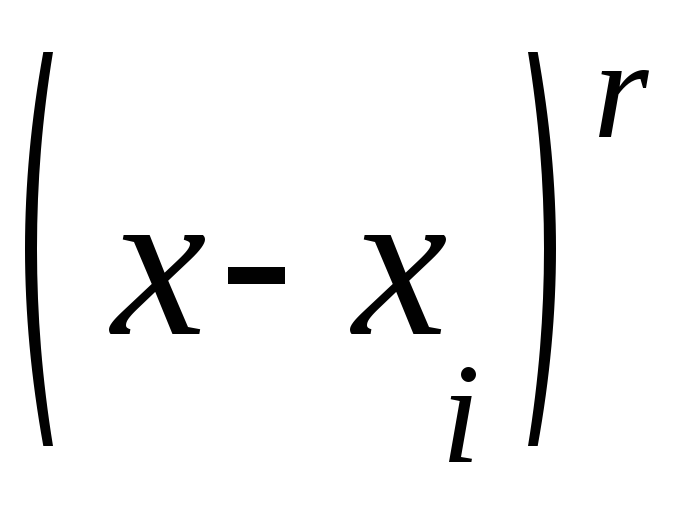 ;
;трёхчленов типа
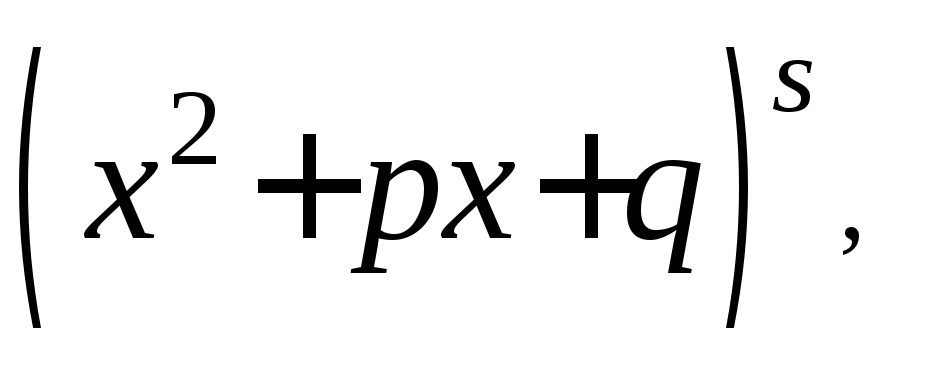
где
![]() ─ действительные числа (причём
─ действительные числа (причём![]() ),
),![]() действительный корень полинома
действительный корень полинома![]() и
и![]() ─ кратности соответствующих сомножителей
при условии, что
─ кратности соответствующих сомножителей
при условии, что![]() .
По отношению к полиному знаменателя
.
По отношению к полиному знаменателя![]() это означает, что подынтегральную
функцию можно представить в виде суммы
дробей типа
это означает, что подынтегральную
функцию можно представить в виде суммы
дробей типа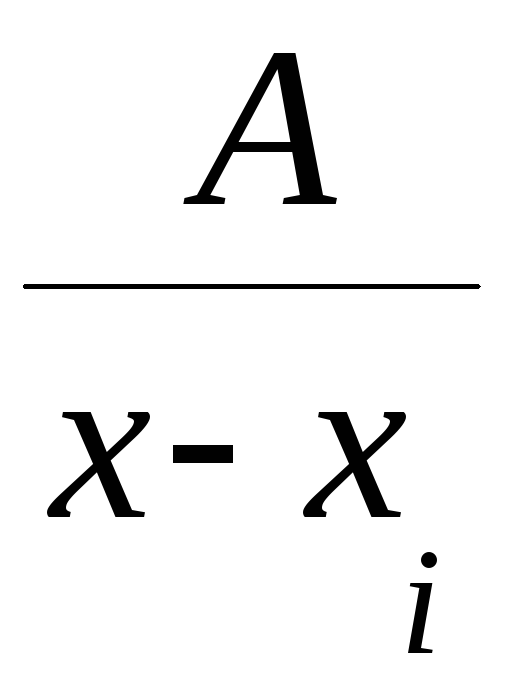 и
и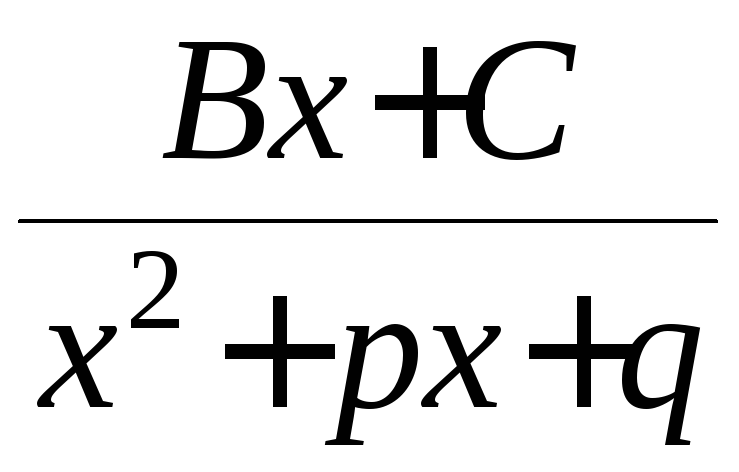 (
(![]() и
и![]() ─ некие числовые коэффициенты) с
соответствующими кратностями (повторами
корней). Тогда нахождение интеграла от
рациональной дроби сведётся к взятию
табличного интеграла типа
─ некие числовые коэффициенты) с
соответствующими кратностями (повторами
корней). Тогда нахождение интеграла от
рациональной дроби сведётся к взятию
табличного интеграла типа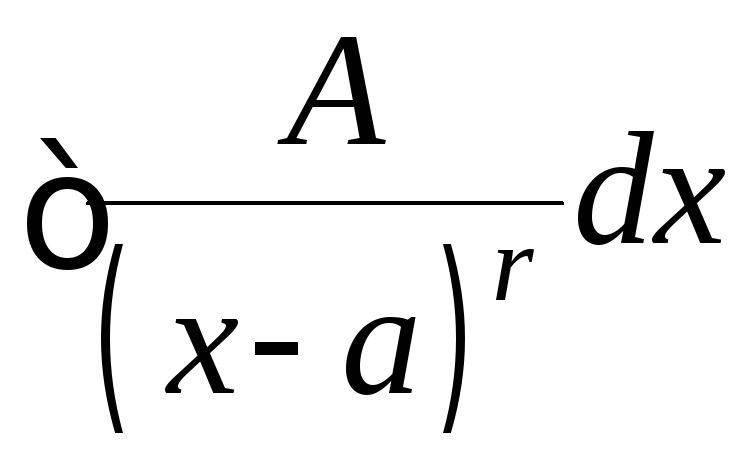 и интеграла типа
и интеграла типа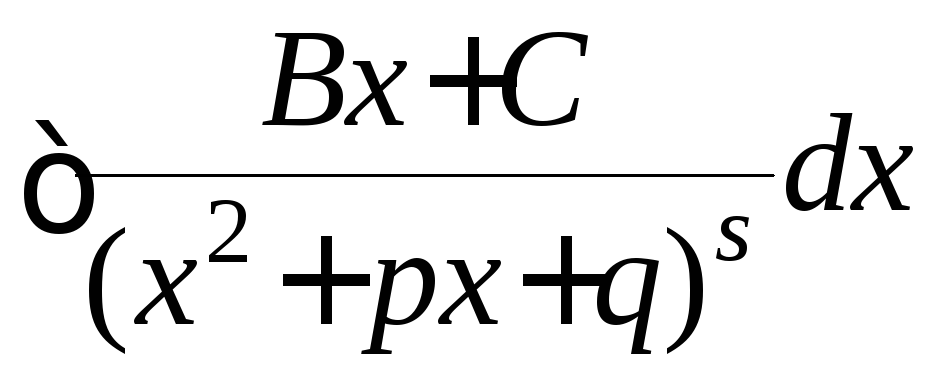 ,
способ решения которого для
,
способ решения которого для![]() =1
рассмотрен в
Примере
2. Остаётся только освоить методику
разложения рациональной дроби на
соответствующие слагаемые.
=1
рассмотрен в
Примере
2. Остаётся только освоить методику
разложения рациональной дроби на
соответствующие слагаемые.
Рассмотрим несколько примеров на эту тему.
Пример
9.
![]()
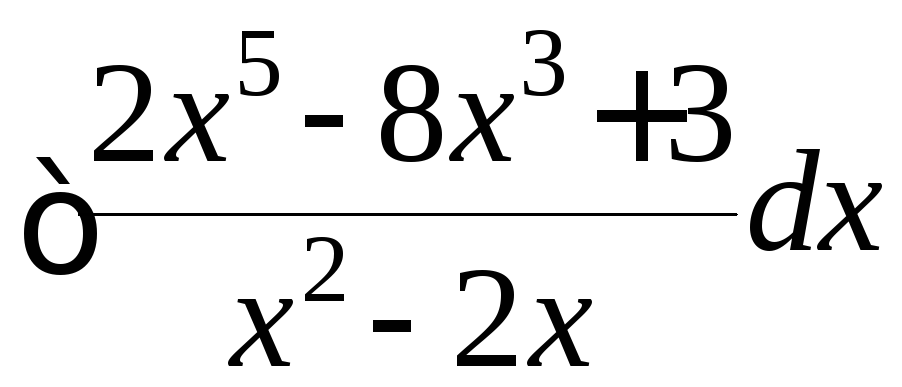 .
.
Рецепт. Здесь порядок полинома числителя больше порядка полинома знаменателя, поэтому делим «столбиком» числитель на знаменатель:

Таким образом,
![]()
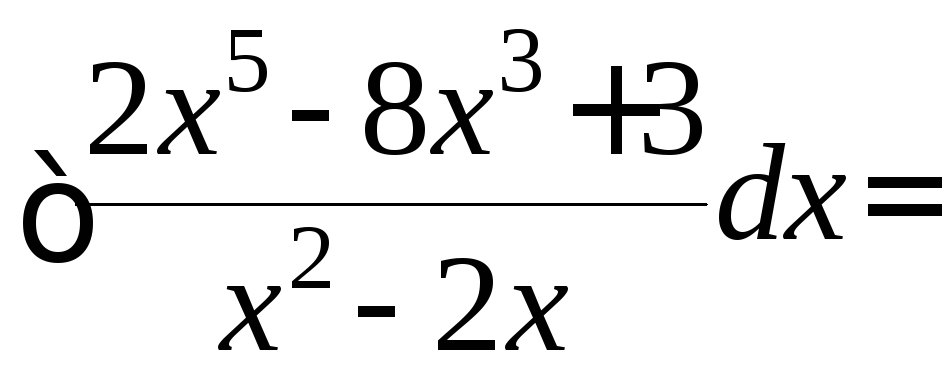
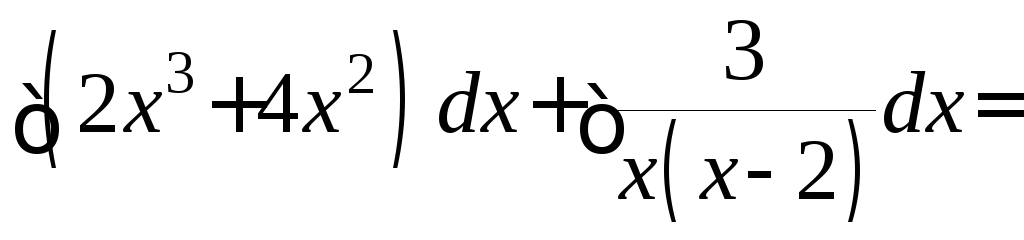
![]() ,
где
,
где
![]() =
=
=
=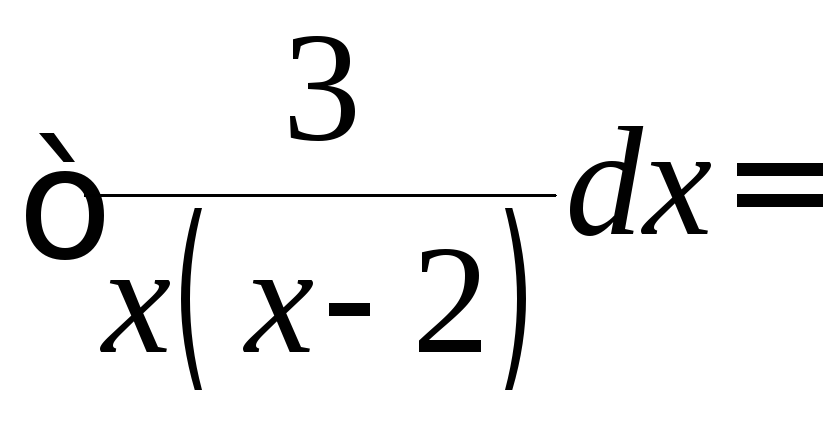
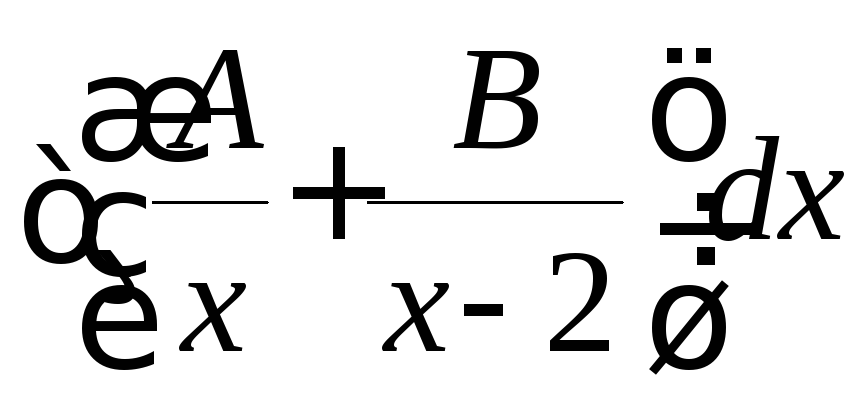 .
Здесь
.
Здесь![]() действительные
числа, которые подбираются следующим
образом:
действительные
числа, которые подбираются следующим
образом:
сложим дроби:
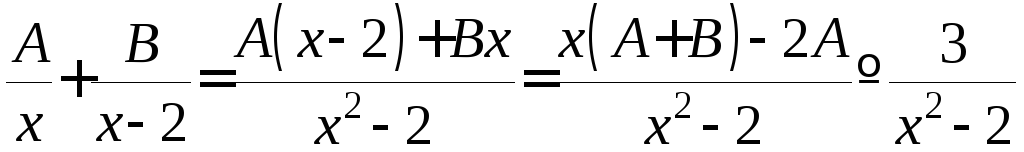 ;
;затем приравняем коэффициенты при соответствующих степенях аргумента и получим систему двух линейных уравнений для
 и
и :
: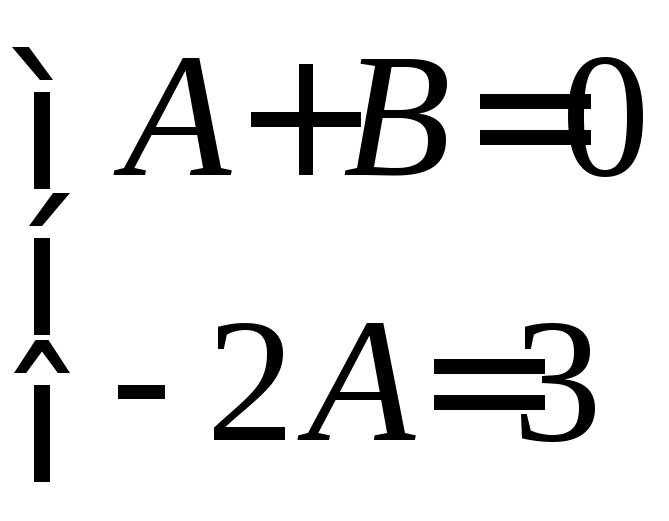 ;
;
тогда решение этой
системы:
![]()
Отсюда интеграл
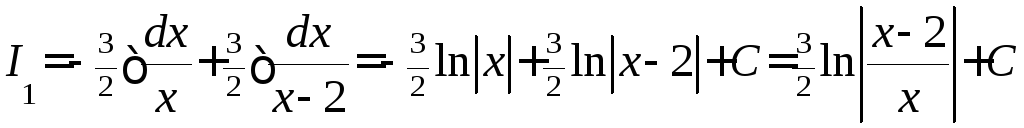 .
.
Таким образом,
общее решение можно представить в
следующем виде
![]()
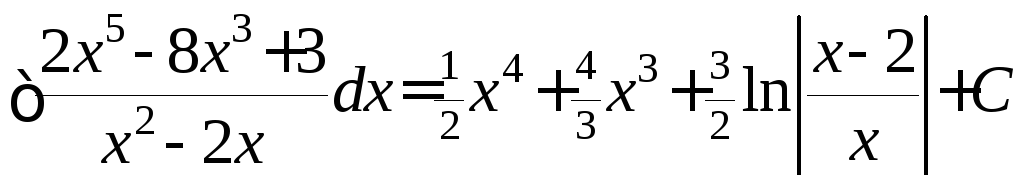 .
.
Пример
10.
![]()
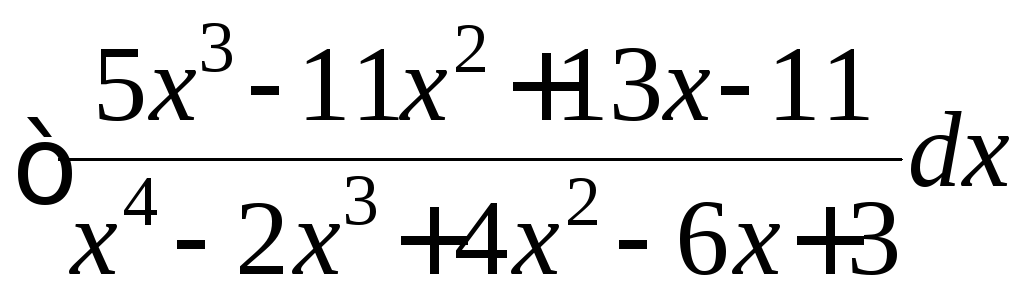 .
.
Рецепт
1. Здесь порядок полинома числителя меньше порядка полинома знаменателя, поэтому не нужно выделять целую часть.
2. В предположении, что данный интеграл можно решить методом неопределённых коэффициентов, попробуем разложить полином знаменателя на множители.
Согласно теореме
Виета, свободный член любого полинома
равен произведению всех
его корней на множитель
![]() ,
где
,
где![]() –
порядок полинома. Здесь
–
порядок полинома. Здесь![]() ,
тогда этот множитель равен единице.
Попробуем подобрать хотя бы один целый
корень, возьмём, например,
,
тогда этот множитель равен единице.
Попробуем подобрать хотя бы один целый
корень, возьмём, например,![]() .
При
.
При![]() значение полинома: 1-2+4-6+3=0, т.е.
значение полинома: 1-2+4-6+3=0, т.е.![]() – один из корней. Теперь поделим исходный
полином «столбиком» (см. выше) на двучлен
– один из корней. Теперь поделим исходный
полином «столбиком» (см. выше) на двучлен![]() и получим полином третьего порядка
и получим полином третьего порядка![]() .
Сгруппируем соответствующие слагаемые:
.
Сгруппируем соответствующие слагаемые:![]() .
Таким образом, подынтегральная функция
должна иметь вид
.
Таким образом, подынтегральная функция
должна иметь вид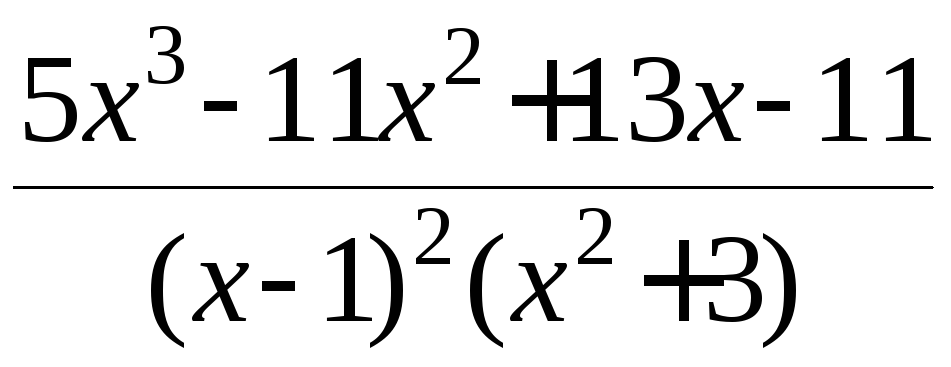 .
В знаменателе имеется двучлен
.
В знаменателе имеется двучлен![]() кратности 2 и «усечённый» трёхчлен
кратности 2 и «усечённый» трёхчлен![]() с
отрицательным дискриминантом. В этом
случае подынтегральную функцию можно
представить в виде суммы дробей:
с
отрицательным дискриминантом. В этом
случае подынтегральную функцию можно
представить в виде суммы дробей: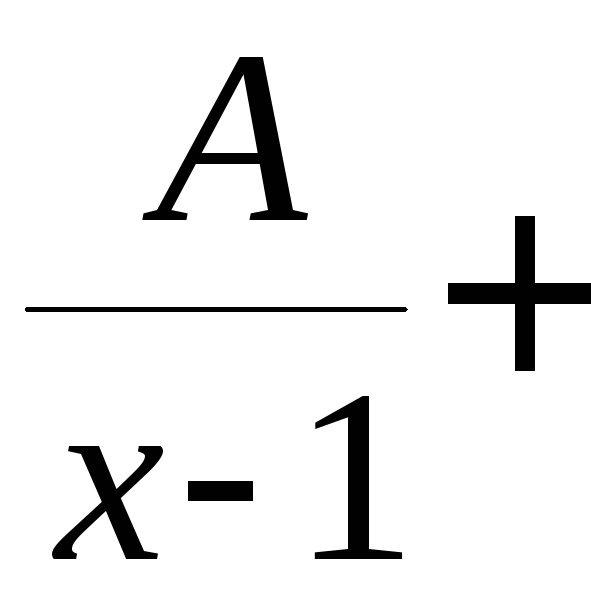
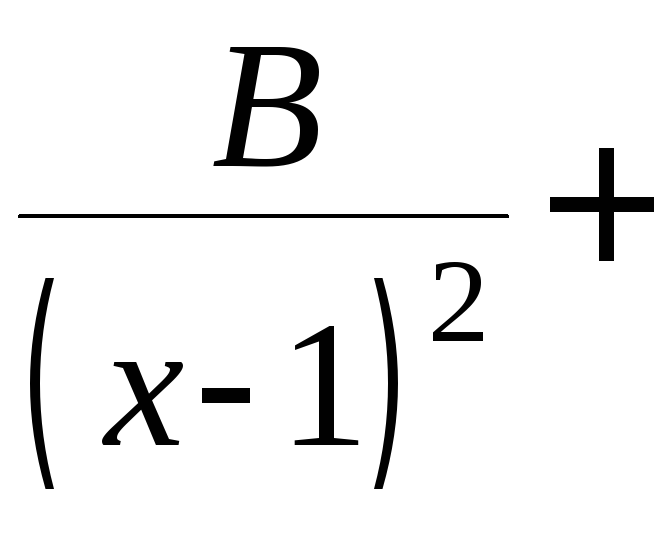
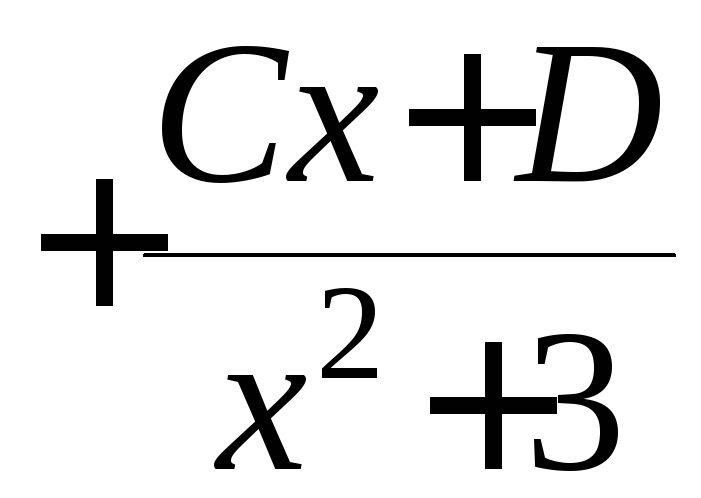 (здесь, как и раньше
коэффициенты
(здесь, как и раньше
коэффициенты
![]() ─ действительные числа).
─ действительные числа).
Обратите, пожалуйста, внимание на тот факт, что порядок полиномов в числителях этих дробей ровно на единицу меньше порядка полиномов в знаменателях!
В результате
сложения этих дробей получаем дробь
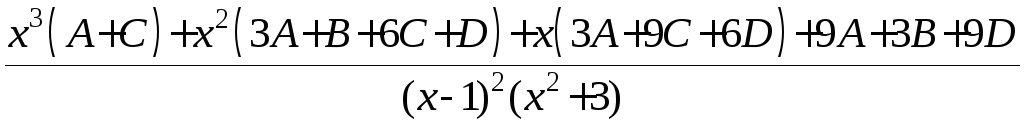 ,
числитель которой должен в точности
совпадать с числителем дроби исходной
подынтегральной функции. Это позволяет
сформировать систему теперь ужечетырёх
линейных
уравнений для этих коэффициентов:
,
числитель которой должен в точности
совпадать с числителем дроби исходной
подынтегральной функции. Это позволяет
сформировать систему теперь ужечетырёх
линейных
уравнений для этих коэффициентов:
 .
.
Нетрудно показать,
что решение этой системы
![]() и исходный интеграл равен сумме трёх
интегралов:
и исходный интеграл равен сумме трёх
интегралов: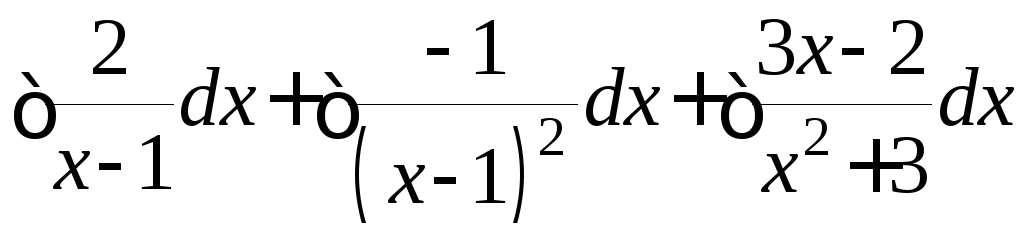 .
Первые два – табличные, и их результат:
.
Первые два – табличные, и их результат: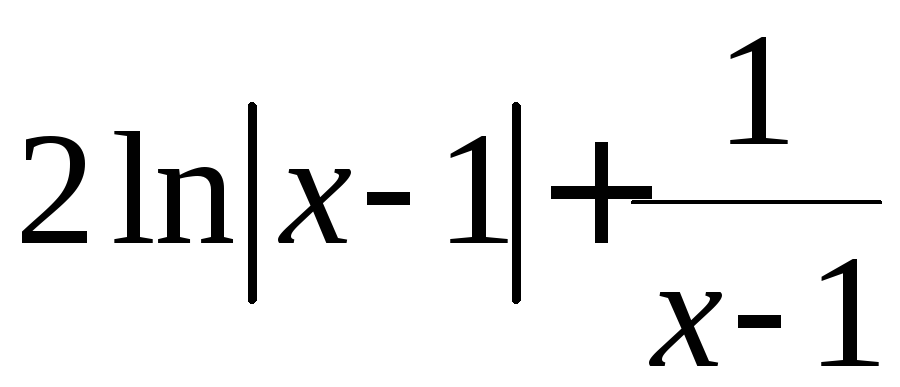 .
Решение последнего интеграла
.
Решение последнего интеграла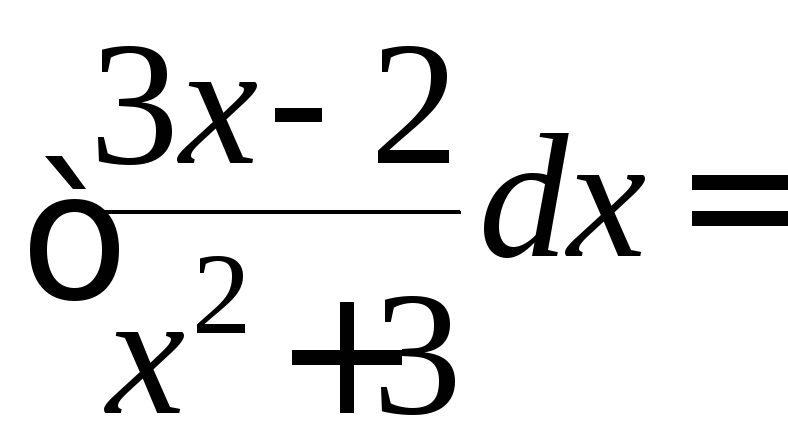
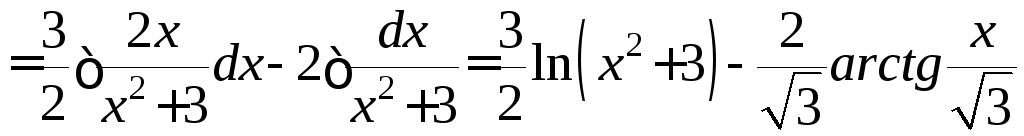 .
Итак, ответ:
.
Итак, ответ:
![]()
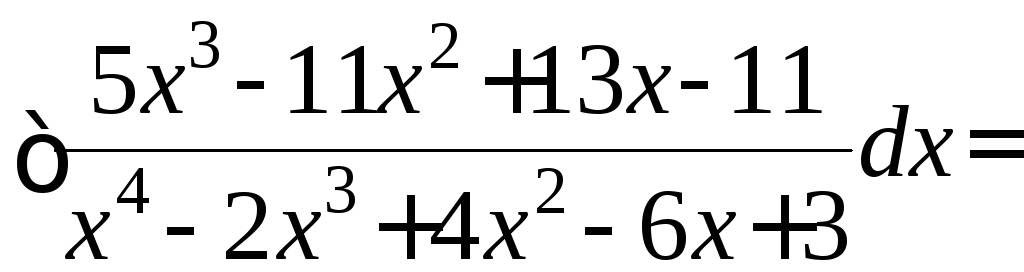
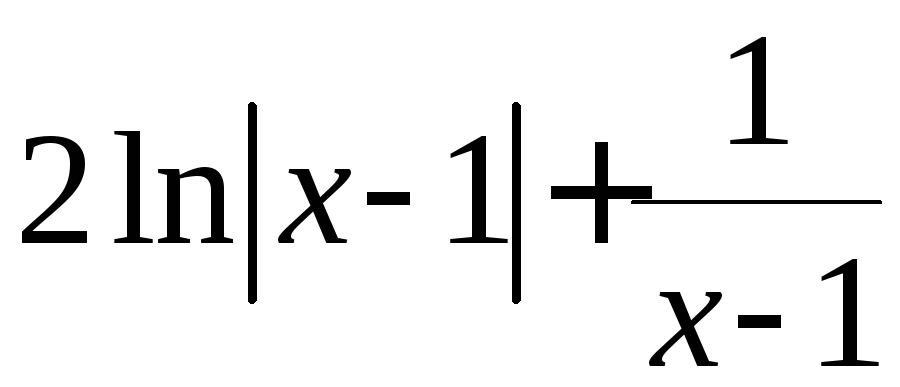
![]()
![]() .
.
Обратите внимание на то, что громоздкий интеграл был сведён к комбинации табличных интегралов (решение последнего интеграла – см. Пример 3).
Пример
11.
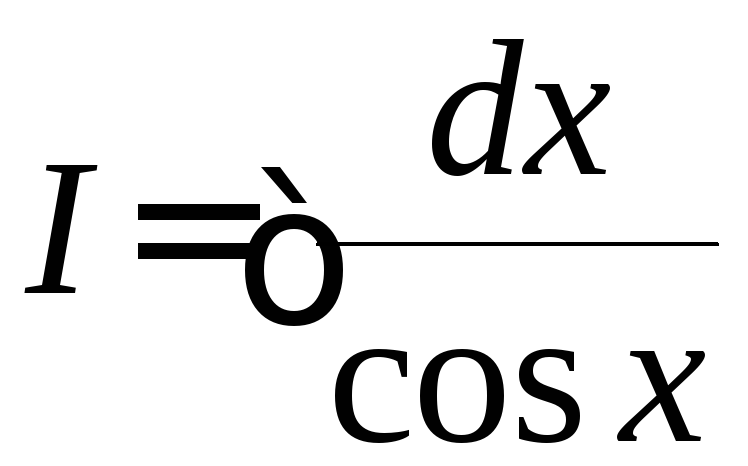 .
.
Рецепт.
Покажем, что этот интеграл можно
достаточно просто решить тем же методом
«неопределённых коэффициентов». Для
этого домножим числитель и знаменатель
на
![]() .
Подынтегральная функция примет вид
.
Подынтегральная функция примет вид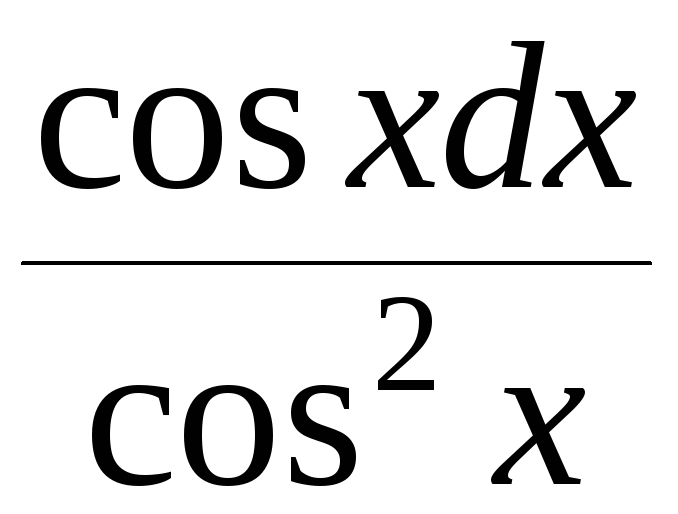 .
Опытный взгляд сразу увидит в числителе
дифференциал функции
.
Опытный взгляд сразу увидит в числителе
дифференциал функции![]() .
Отсюда возникает желание ввести замену:
.
Отсюда возникает желание ввести замену:![]() .
Далее подставляем эти выражения в
подынтегральную функцию, и интеграл
приобретает следующий вид:
.
Далее подставляем эти выражения в
подынтегральную функцию, и интеграл
приобретает следующий вид: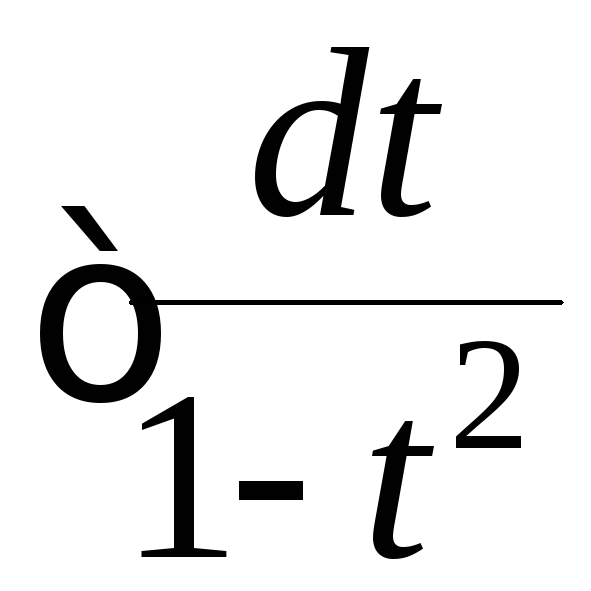 ─ и готов к приложению к нему метода
«неопределённых коэффициентов»:
─ и готов к приложению к нему метода
«неопределённых коэффициентов»: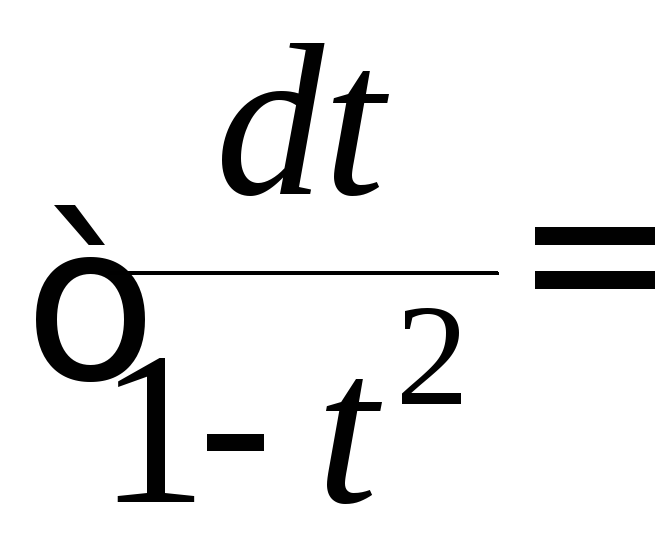
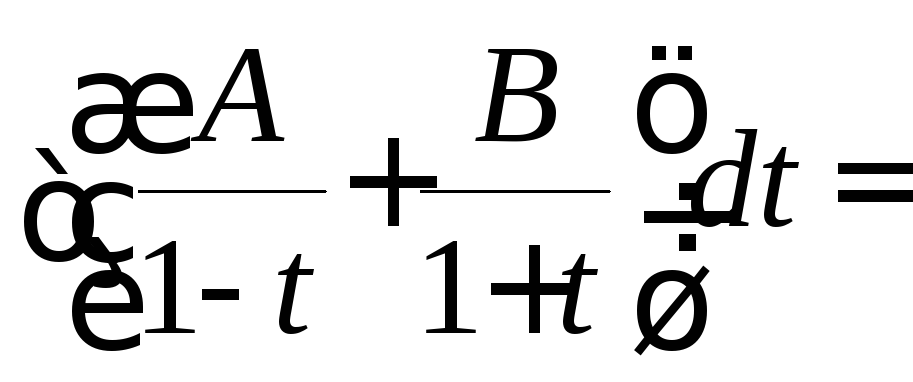
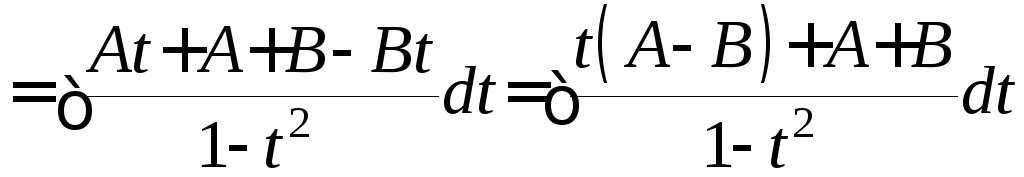 .
Знакомым уже способом получаем систему
уравнений:
.
Знакомым уже способом получаем систему
уравнений: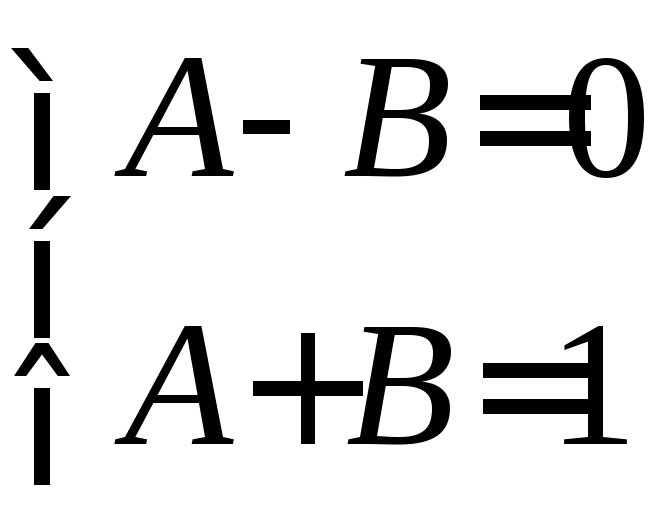 .
Из решения системы следует:
.
Из решения системы следует: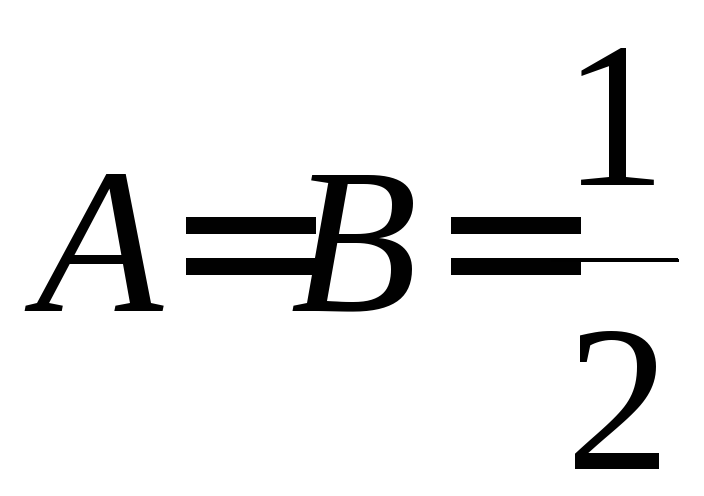 и
и .
После обратной подстановки
.
После обратной подстановки![]() получаем окончательный результат:
получаем окончательный результат: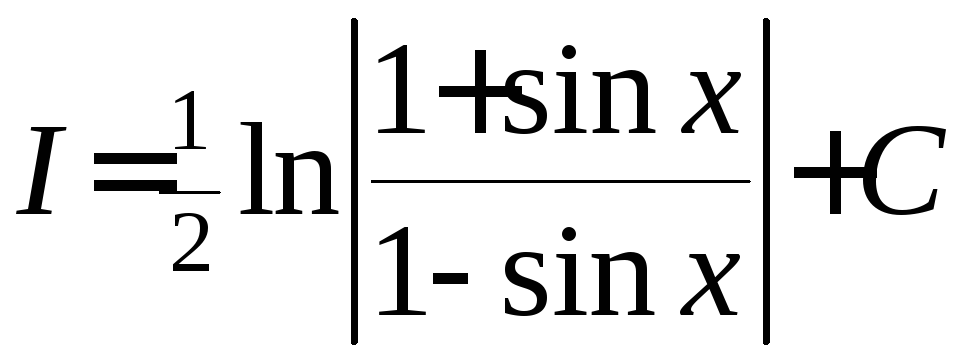 .
.
Это очень полезный результат, поэтому есть смысл записать его в дополнительную таблицу неопределённых интегралов (см. табл.2).
Легко показать,
что аналогичный интеграл
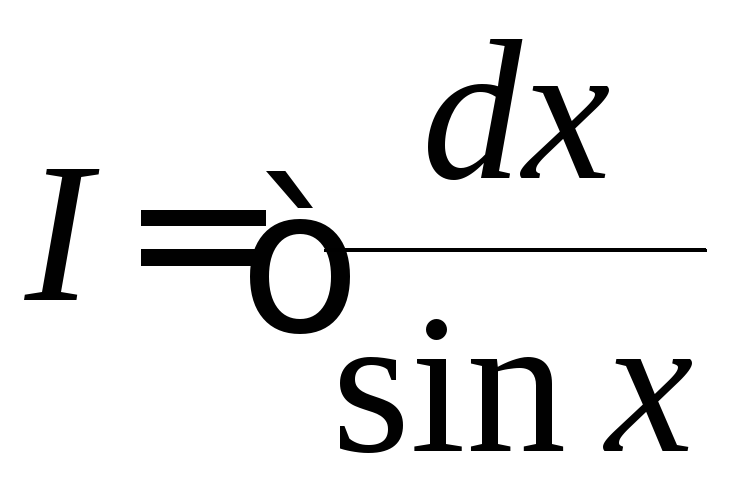 =
=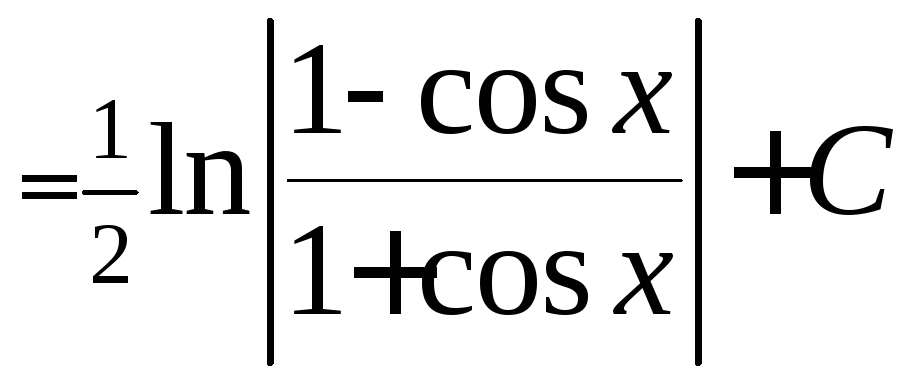 .
С учётом формул
.
С учётом формул![]() и
и![]() получаем ещё один вариант решения этого
интеграла:
получаем ещё один вариант решения этого
интеграла: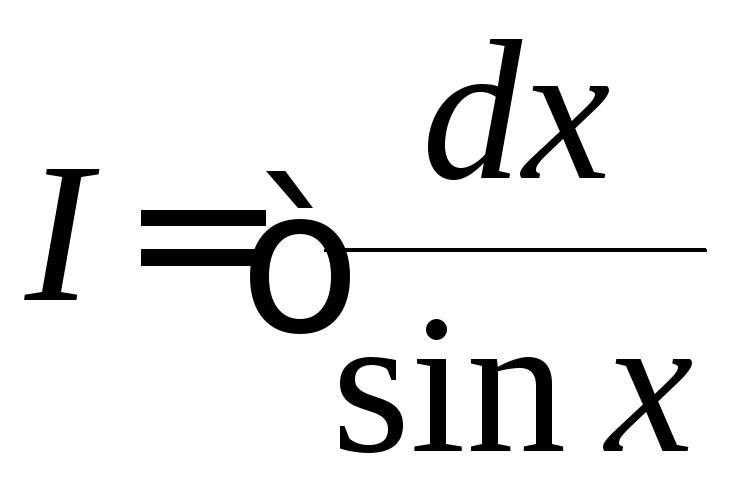 =
=![]() +С.
И этот результат рекомендуем внести в
ту же дополнительную таблицу.
+С.
И этот результат рекомендуем внести в
ту же дополнительную таблицу.
N.B. Несколько позже мы рассмотрим решение этого же интеграла другим способом.
