Непрерывные функции

1

ЛЕКЦИЯ 6. НЕПРЕРЫВНОСТЬ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Непрерывность функции в точке

Односторонняя непрерывность справа и слева, связь с непрерывностью в точке

Классификация точек разрыва. Примеры

Свойства непрерывных функций:

теорема о локальной ограниченности;

теорема об устойчивости знака непрерывной функции в точке

Арифметические операции над непрерывными функциями. Непрерывность многочлена и дробно-рациональной функции

Теорема о непрерывности сложной функции

Непрерывность элементарных функций

6. 1 Непрерывность функции в точке

Определение. Функция f : X R называется непрерывной в точке x0

(x0– предельная точка X), если существует

	lim f x f x0 .					(1)
	x x0
Обратим внимание на то, что условиями непрерывности функции в точке
x0 (при записи соотношения (1)) являются:
1) существование конечного значения f x0 ;
2) существование конечного	lim	f x .
	x x0
		f x f x0 f
Так как lim x x0 , то	lim			x		. Следовательно,
			lim
x x0	x x0		x x0

непрерывные в точке функции (и только они) перестановочны с операцией предельного перехода (т. е. можно переходить к пределу под знаком функции):

	f x f
lim			lim	x
					.
x x0		x x0

Определение. В изолированной точке x0 любая функция f непрерывна.

1

2

Определение. Функция f x , не являющаяся непрерывной в точке x0 ,

предельной для X , называется разрывной в ней. Точку x0 называют точкой разрыва функции f x , причем функция f x может быть не определена в

этой точке.

Подставляя сюда определения предела по Коши или по Гейне, получим:

Определение непрерывности функции в точке по Коши: функция

f не-

прерывна

в

точке

x0 ,

если

0 , x0 0 x X (

x x0

f (x) f (x0)

).

f

Определение непрерывности функции в точке по Гейне: функция

не-

прерывна в точке x

, если x

x

lim

f x

f x

X lim x

.

0

n

n n

0

n

n

0

6.2 Односторонняя непрерывность, связь с непрерывностью в

точке

Из связи существования предела и односторонних пределов получаем:

Определение. Функция

f : X R называется

непрерывной

слева

(справа) в точке x0 X , предельной для множества X , если

f x0 0 f x0 f x0 0 f x0 .

Критерий непрерывности функции в точке через односторонние пределы

Функция f : X R непрерывна в точке x0 X , предельной для множе-

ства X , тогда и только тогда,	когда она непрерывна в этой точке и слева и
справа, то есть	0 f x0 f x0 0 .
f x0		(2)
Положим	y f x0 : f x0 x f x0 .
x: x x0,

Величину x называют приращением аргумента, а y – приращением

функции. Так как x x0 x, то условие непрерывности (1) можно переписать

в виде lim	f x	x	f x	. Отсюда lim	f x	x f x	0 или
x 0		0	0	x 0	0	0
				lim f x0 0			(3)
				x 0

Равенство (3) называется разностным условием непрерывности функции в точке и служит практическим приемом доказательства непрерывности функции в точке.

2

3

Пример. Покажем, что функция f x x3 непрерывна в любой точке

x0 R.

Имеем lim f x

x 0 0

lim x0 x 3 x0	3 lim x0 x x0 x0 x 2 x0 x0 x x0						2
x 0	x 0
lim x x0 x 2 x0 x0 x x0		2 0.
x 0
Значит, функция f x x3 непрерывна во всякой точке x				0	.
6.3 Классификация точек разрыва. Примеры
Пусть функция	f : X R, x0 X – предельная точка для множества X .
Определение. Если существует lim f x A,			A f x0			( f x0
		x x0

может вообще не существовать), то точка x0 называется точкой устранимого

разрыва.

Замечание. В случае устранимого разрыва

f x0 0 f x0 0 f x0 . Указанный разрыв можно устранить, если допол-

нить разрывную функцию до непрерывности следующим образом:

	f x ,		x x	0		,
f x		,	x x				.
	f x				0
		0

Пример. Функция y

sin x

имеет в точке x 0 устранимый разрыв, так

x

как y 0 y 0 1:

lim

sin x

1. Здесь y 0 не существует.

x 0 x

1

y

sin x

x

х

0

sin x

Если положить y 0 1

,

x 0,

, то получим непрерывную функцию y

x

1,

x 0.

3

									4
	Определение. Если существуют конечные односторонние пре-
делы	f x0 0 ,				f x0 0 , не равные между собой f x0 0 f x0 0 (зна-
чение	f x0 может также не существовать), то точка x0									называется точкой раз-
рыва 1 - го рода.
	Число		f x0		0 f x0 0			называется скачком функции f в точке x0 .
	Во всех остальных случаях точку разрыва x0 будем называть точкой раз-
рыва 2 - го рода.
	Замечание. В случае разрыва 2 - го рода хотя бы один из односторон-
них пределов бесконечен или вообще не существует.
	Если односторонние пределы								f x0 0 или f x0	0 бесконечны, то
точку x0 иногда называют полюсом.
					1,				x 0,	у
						0,			x 0,	1
	Примеры. 1. y sgnx
						1,			x 0.	0
										х
Здесь точка x0				- точка разрыва первого ро-
да: y 0 1,				y 0 1. Заметим, что

скачок функции в этой точке равен y 0 y 0 1 1 2.

2. Функция y sin 1 имеет в точке x 0 разрыв второго рода, так как x

lim sin 1 не существует (см. пример ).

x 0 x

														1
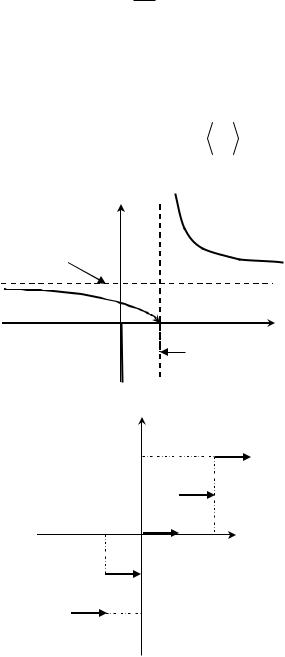
		3. Исследуем поведение функции											y 2x 1.
			1					1				2
	lim	2x 1					x 1 0,						0.
								x 1
	x 1 0
				1				1				2
	lim	2x 1					x 1 0,						.
								x 1
	x 1 0

4

5

1

Функция y 2x 1 имеет в точке x 1 разрыв второго рода. Прямая является правой вертикальной асимптотой графика функции (см.).

Исследуем поведение функции на бесконечности:

1

x 1

1

0

20

lim 2x 1

1. Поэтому прямая y 1 является горизон-

x

x 1

тальной асимптотой графика функции (см. ) Построим график функции:

Здесь

у

1

y 0

, y 1 0 0, y 1 0 .

y 1

2

0

1

х

4. Исследуем поведение

x 1

функции

у

f x E x x k,

k x k 1.

Здесь

1

f k f k 0 k,

f k 0 k 1.

Точки x k Z – точки разрыва перво-

х го рода. Функция непрерывна справа в

2

1

0

точках x k .

6.4 Свойства непрерывных функций

ТЕОРЕМА 1 (о локальной ограниченности)

Если функция непрерывна в точке, то она ограничена в некоторой окре-

стности этой точки.

Пусть f : R, x0 .

ТЕОРЕМА 2 (об устойчивости знака непрерывной функции в точке)

5

6

Если

функция

f

непрерывна

в точке

x0

и

f x0 0,

то x0

x x0 sgn f x sgn f x0 .

В самом

деле,

так

как

f x непрерывна

в

точке x0 ,

то

существует

lim

f x f x

. Тогда x

x x

f x

f x0

.

0

0

0

x x0

2

При этом

f x

f x0 , если

f x

0, и f

x

f x0 , если

f x 0.

2

0

2

0

Отсюда вытекает,

что,

если функция

f

непрерывна

в

точке x0 и

f x0 0, то она сохраняет знак в некоторой окрестности точки x0 .

Следствие. Пусть

f , g: X R,

x0 X ,

f

и g

непрерывны в точке x0

и f x0 g x0 . Тогда x0 : x x0

f x g x .

Доказательство. Рассмотрим h x : f x g x ,

h x непрерывна в точ-

ке

x0 ,

h x0 0

x0 :

x x0 h x 0 f x g x

x x0 .

6.5 Арифметические операции над непрерывными функциями

ТЕОРЕМА 3. Сумма и произведение непрерывных функций непрерыв-

ны: если функции f , g: R непрерывны в точке x0 X , то функции f g

и f g также непрерывны в этой точке.
Доказательство.
1.	Пусть x0 – изолированная точка. Тогда f g и	f g непрерывны

по определению.

2.Пусть x0 – предельная точка множества Х. Тогда

lim f x g x	lim	f x lim	g x f x0 g x0 ;
x x0	x x0	x x0	g x f x0 g x0 .
lim f x g x	lim	f x lim
x x0	x x0	x x0
		6

7

ТЕОРЕМА 4. Функция

1

непрерывна в точке x

,

если функция

f

не-

f

0

прерывна в точке x0 и

f x0 0.

Следствие. Функция

g

непрерывна в точке

x ,

если функции

f

и g

f

0

непрерывны в точке x0

и f x0 0.

6.6 Теорема о непрерывности сложной функции

ТЕОРЕМА 5 . Пусть f : , g: ,

функция f

непрерывна в

точке x0 , f x0 : y0

и функция g непрерывна в точке

y0 .

Тогда сложная

функция h x g f x непрерывна в точке x0 .

В самом деле,

lim f x f x0 y0,

(1)

x x0

lim g y g y0 ,

x x0

g f x g y0 .

но тогда согласно теореме о пределе композиции функций

lim

x x0

Из (1) вытекает, что lim

g f x g f x0 . Теорема доказана.

x x0

Следствие. Если

lim f x y0, а g y непрерывна в точке y0 , то

x x0

lim g f x g y0 g lim f

x .

x x0

x x0

Итак, для непрерывной функции переход к пределу можно выполнять под знаком функции.

6.7 Непрерывность элементарных функций

Перечислим основные элементарные функции: x		(x 0, R), ax
(a 0, a 1), loga x	(a 0, a 1), sin x, cosx, tgx, ctgx,	arcsinx, arccosx,
arctgx, arcctgx.

7

8

Определение. Функции, полученные из основных элементарных функ-

ций с помощью конечного числа арифметических операций и операций супер-

позиции, называются элементарными.

	logtg x	x 2x
Пример. Функция f x e			, x 0,1 является элементар-
		arcsin x

ной.

Среди элементарных функций обычно выделяются:

целая рациональная функция или многочлен

Pn x a0xn a1xn 1 an 1x an,

здесь n – степень многочлена, n N; a0, a1, , an R – коэффициенты

многочлена; дробно-рациональная функция, являющаяся отношением двух многочленов

P x f x Qn x .

m

Целые рациональные и дробно-рациональные функции образуют так назы-

ваемый класс рациональных функций.

К элементарным функциям относят также те иррациональные функции, которые представляют суперпозицию рациональных функций и степенных функций с дробно-рациональными показателями.

Рациональные и иррациональные функции образуют класс алгебраических функций. Элементарные функции, которые не являются алгебраическими, на-

зываются трансцендентными функциями.

Примеры: а)				f x 4x5 3x2 x 6 – целая рациональная функция,
или многочлен пятой степени;
б)	f x		3x4 x2 5							– дробно-рациональная функция;
			x3 2x 3
	f x		x2						– иррациональная функция;
в)						x
			3 3
					x
г)	f x cosx,				y x sin x, u x ex – трансцендентные функции.

ТЕОРЕМА. Элементарные функции непрерывны в каждой точке своей области определения.

Доказательства вытекает из определения и теорем 3 - 5 (Свойства непрерывных функций).

8

9

Пример. Покажем, что функция f x sinxнепрерывна в любой точке

x0 R.

Требуется доказать, что

0 0 x(

x x0

sinx sinx0

).

Лемма. x R

sin x

x

.

M

x

A

O

sin x: ордината точки M .

																													1
				1. Пусть x							0,							. S			OAM										1 sin x S			сектораOAM
															2															2
x		0,				.
					2
				2. Пусть x														,0		x										0,			.
															2																	2
	sinx			sinx sin x x																				x			.
				Итак,				sin x					x		,			x							,					\ 0 .
																						2						2
				3. Ясно, что sin 0															0.

x , то есть sinx x,

2

4. Пусть

x

. В этом случае

sin x

1

x

. Таким образом,

2

2

sin x x x R.

Лемма доказана.

Возьмем любое положительное 0. Оценим модуль разности

sinx sinx0

9

10

x x0

x x0

sinx

x

cosx

x x0

2 sin

cos

,

1

2

1

x x

0

.

2

2

2

. Тогда

Пусть

x R:

x x0

sin x sin x0

. Таким

образом, функция y sin x

непрерывна в каждой точке x0 R .

Пример 2.

y sin x,

x

,

. Функция

y sin x непрерывна и строго

2

2

,

возрастает на

. Поэтому существует обратная функция, которую обо-

2

2

значают

x arcsin y

,

определенная на

sin

,sin

1,1 , возрастающая

2

2

на 1,1 от

до

и непрерывная на этом отрезке.

2

2

Пример 3.

y f x g x ,

f x 0, f и g непрерывны на множестве Χ .

y eln f x g x

непрерывна по теореме 5.

В частности, y x ,

R, непрерывна x R.

Пример 4. Так как для непрерывной функции переход к пределу можно

выполнять под знаком функции, то

g x lim

ln f x

f x lim g x

lim f x g x

lim

ln

lim

lim

eg x ln f x ex x0

x x0

e

x x0

x x0

x x0

x x0

lim g x

x x

0

.

lim

f x

x x0

10