ПП _02 _Алгебра событий_Классическое опр вер

	пользованными}?
	РЕШЕНИЕ:					=10!2! =1814400 ,
	Общее число способов N (Ω)= A108
	N (A)= A88 =8!,	P (A)	=	N (A)	= 8! 2!	=	1	= 0,0(2).
				N (Ω)
					10! 45
ПП 2.2.	Три неразличимых шара случайным образом разме-
№15	щаются по трем ящикам. Изобразите пространство
	исходов опыта, приведя все способы возможных
	размещений.
	РЕШЕНИЕ:
	Если шары неразличимы, пространство событий
	имеет 10 исходов:
	1. {111,-,-}	6.	{1,11,-}
	2. {-,111,-}	7.	{1,-,11}
	3. {-,-,111}	8.	{-,11,1}
	4. {11,1,-}	9.	{-,1,11}
	5. {11,-,1}	10. {1,1,1}
ПП 2.2.	Три различных шара случайным образом размеща-
№16	ются по трем ящикам. Изобразите пространство ис-
	ходов опыта, приведя все способы возможных раз-
	мещений.
	Найдите вероятности событий:
	А – существует ящик, содержащий не менее двух
	шаров;
	В – первый ящик не пуст;
	С – первый ящик пуст и не существует ящика, со-
	держащего более одного шара.
	РЕШЕНИЕ:								0,(7),
	Пространство размещений A{Ai }:
	A1 {abc,-,-}		A10 {a,bc,-}				A19 {-,a,bc}		0,70(37),
	A2 {-,abc,-}		A11 {b,ac,-}				A20 {-,b,ac}		0
	A3 {-,-,abc}		A12 {c,ab,-}				A21 {-,c,ab}
	A4 {ab,c,-}		A13 {a,-,bc}				A22 {a,b,c}
	A5 {ac,b,-}		A14 {b,-,ac)				A23 {a,c,b}
	A6 {bc,a,-}		A15 {c,-,ab}				A24 {b,a,c}
	A7 {ab,-,c}		A16 {-,ab,c}				A25 {b,c,a}
	A8 {ac,-,b}		A17 {-,ac,b}				A26 c,a,b}
	A9 {bc,-,a}		A18 {-,bc,a}				A27 {c,b,a}
	Число исходов Ai : N(Ω)=33=27.
	Вероятность каждого из них равна

11

Р( Ai ) = 271 (i = 1, 2, …, 27).

Каждое из размещений Ai является элементар-

ным событием.

1) Событию А соответствуют элементарные исходы:

{A1, A2 ,...A21}, N(А) = 21, P(А) = NN((ΩA)) = 2721 = 0,(7).

2) Событию B соответствуют элементарные исходы:

{A1; A4 , A5...A15 ; A22 , A23...A27 },

N(B) = 19, P(B) = NN((ΩA)) = 1927 = 0,70(37).

Множество исходов события С пусто,

Р(С) =

N (C)

= 0.

N (Ω)

Имеется r шаров, которые наудачу размещаются по п

ящикам. В одном и том же ящике могут находиться

несколько шаров и даже все шары. Найдите формулу

для вычисления вероятности того, что в первый ящик

попадет ровно r1 шар, во второй – r2 и т.д. (r1 + r2 + …

+ rr = r).

а) Вычислите вероятность того, что в один ящик

попадет ровно один шар, во второй – два, в следую-

щий – три и т.д., если 10 шаров нужно распределить

таким образом по 20 ящикам.

б) Какова вероятность того, что каждый ящик за-

нят, если число шаров равно количеству ящиков и

равно семи?

ПП 2.2.

РЕШЕНИЕ:

а) 8 10−41 ;

Каждый шар может находиться в каждом из п

№17

ящиков, значит r шаров можно распределить по

б) 0,00612

ящикам пr различными способами. Число благопри-

ятных исходов подсчитываем следующим образом:

число способов, которыми можно выбрать r1 шаров

из r, равно Crr1 , число способов, которыми можно вы-

брать r2 шара из (r-r1) оставшихся шаров, равно Crr2−r

и т.д. Все эти числа нужно перемножить.

1

Вероятность равна:

r1

r2

rn-1

− (r1 + r2 +... + rn

- 2)

r!

P=

Cr

Cr-r1

... Cr

=

nr

nr ! ... r !

n

а) Если 10 шаров нужно распределить по 20 ящикам,

то r =10, п = 20. Вероятность того, что в одном ящи-

ке будет 1 шар, в другом 2 шара, в следующем – 3 и

т.д., равна:

12

P =

N (A)

=

C1

C2

C3

C

4

=

10!

=

10

9

7

4

N (Ω)

10

10

1!2!3!4!

20

20

=

10 9 4 7 5 ≈ 8 10−41

2010 2

б) Если число шаров равно числу ящиков, то r = n.

В этом случае N(Ω) = nn. Событие А заключается в

том, что каждый ящик занят.

N(А) = n(n -1) … 1 , P(A)=

N ( A)

=

n!

.

N (Ω)

nn

При п =7 вероятность этого равна: Р(А) = 0,00612.

Имеется r шаров, которые размещаются по п ящи-

кам. Найдите формулу для вычисления вероятности

того, что фиксированный ящик содержит ровно k

шаров.

Какова вероятность того, что при размещении семи

шаров по десяти ящикам в одном из них оказалось

три шара?

РЕШЕНИЕ:

r шаров по п ящикам можно разместить п r различ-

ПП 2.2.

ными способами: k шаров из r можно выбрать Crk

способами, а оставшиеся (r – k) шаров можно раз-

35 10-10

№18

местить в оставшихся

(п – 1) ящиках (п – 1)(r – k) способами, поэтому иско-

мая вероятность равна

C k (n −1)r −k

P(A) =

N (A)

=

r

N (Ω)

nr

Если 7 шаров размещать по 10 ящикам так, чтобы в

одном из них оказалось 3 из них,

то вероятность та-

кого разбрасывания равна

P =

7!

=

7 6 5

= 35 10-10 .

3! 4! 107

3 2 107

Случайно размещаем шары по 10 ящикам, пока неко-

торый шар впервые не попадет в уже занятый ящик.

Найдите вероятность того, что процесс закончится на

пятом шаре.

РЕШЕНИЕ:

ПП 2.2.

5 шаров по 10 ящикам можно разложить (с повторе-

ниями) 105 способами. Число способов реализации

0,0084

№19

интересующего нас распределения шаров (3 ящика

содержат по 1 шару, 1 ящик содержит 2 шара, 6 ящи-

ков пустые)

10!

4!

=10 9 8 7 4 =840

N (A)=C4 C1

=

10

4

4! 6! 3! 1!

2 3 4

( из 10 ящиков выбираем 4 заполненных,

13

из 4 заполненных выбираем ящик, содержащий 2

шара).

P(A)=

N (A)

=

840

= 0,0084 .

100000

N (Ω)

Какова вероятность, что в четырех бросаниях иг-

ральной кости а) единица не появится ни разу;

б) единица появится?

ПП 2.2.

РЕШЕНИЕ:

5 .

а) 0,482

№20

При однократном бросании p1 = 1

, q1 =1 − p1 =

б) 0,518

6

6

P (A)= 5 4 ≈ 0,482 , P (B)=1 − P (A)≈ 0,518 ≈0,482 .

6

Найдите вероятность того, что при шести бросаниях

ПП 2.2.

кости появится 1.

РЕШЕНИЕ:

0,665

№21

5

6

P =1 −

≈ 0,665 .

6

Какова вероятность того, что при шести бросаниях

ПП 2.2.

игральной кости выпадут все грани?

0,0154

РЕШЕНИЕ:

№22

N (Ω)=66 , N (A)=6!, P(A)=

6!

≈0,0154 .

6

6

Игральная кость подбрасывается два раза. Какова ве-

роятность, что сумма очков 6?

РЕШЕНИЕ:

Множество исходов опыта содержит 36 элемен-

тарных исходов:

ПП 2.2.

Ω = {{1,1}, {1,2}, {1,3}, {1,4}, {1,5}, {1,6},

0,13(8)

№23

{2,1}, {2,2}, {2,3}, {2,4}, {2,5}, {2,6},

{3,1}, {3,2}, {3,3}, {3,4}, {3,5}, {3,6},

{4,1}, {4,2}, {4,3}, {4,4}, {4,5}, {4,6},

{5,1}, {5,2}, {5,3}, {5,4}, {5,5}, {5,6},

{6,1}, {6,2}, {6,3}, {6,4}, {6,5}, {6,6}}.

Событие А {{1,5}, {2,4}, {3,3}, {4,2}, {5,1}}.

14

Число равновозможных элементарных исходов: N (Ω)=36 , число элементарных исходов, соответст-

вующих событию А: N (A)=5 .

По определению вероятности

P (A)= NN ((ΩA)) = 365 =0,13(8).

Бросаются две игральные кости. Какова вероятность выпадения 1 по крайней мере на одной кости?

РЕШЕНИЕ:

	ПП 2.2.	0,306
	№24

	P = 11 ≈ 0,306 .
	36
ПП 2.2.	Бросили две игральные кости и подсчитали сумму	P(7)> P(8)
№25	выпавших очков. Что вероятнее - получить в сумме
	7 или 8?

15

	P (7)=	6	, P (8)=	5	, P(7)> P(8).
				36
	36
	Найдите вероятность того, что при бросании трех иг-
	ральных костей «6» выпадет на одной любой кости, а
	на двух других выпадут числа, не совпадающие меж-
	ду собой и не равные «6».
	РЕШЕНИЕ:
	Игру в кости можно рассматривать как разме-
	щение r неразличимых (r = 3 кости) шаров
	по п (п = 6 цифр) различным ящикам.
	Общее число элементарных исходов опыта вида
	{1, 1, 1}, {1, 1, 2} … и т.д., равно N(Ω) = 63 = 216.
	Число исходов, благоприятствующих наступлению
	интересующего нас события, можно сосчитать непо-
	средственно, если вычислить число исходов вида {6,
ПП 2.2.	x, y}, учитывая, что одна цифра фиксирована и среди
	х, у отсутствует «6»:			0,093
№26

	N(A) = 20,	P(A) =	N( A)	=	20	=	5	=0,093 .
					216
			N (Ω)			54
ПП 2.2.	Найдите вероятность того, что при бросании трех иг-								0,00463
№27	ральных костей выпадет максимальное число очков.
	РЕШЕНИЕ:
		16

1

3

1

≈ 0,00463.

P =

=

6

216

Наудачу выбирается пятизначное число. Какова ве-

роятность следующих событий:

A {число одинаково читается как слева направо, так

и справа налево};

ПП 2.2.

B {число кратно пяти};

0, 01

;

C {число состоит из нечетных цифр}?

0,5;

№28

РЕШЕНИЕ:

0,035

N (Ω)=9 10 10 10 10 ; N (A)=9 10 10 1 1;

N (B)=9 10 10 10 2 ; N (C )=5 5 5 5 5 .

P(A) = 0,01; P (B)= 1 =0,5; P (C )=

5

=0,035.

5

144

На пустую шахматную доску, случайным образом

ставят две ладьи: белую и черную. Какова вероят-

ность того, что они не побьют друг друга?

РЕШЕНИЕ:

Рассчитаем количество полей, на которых постав-

ленная первой ладья “бьет” другую фигуру. Сделаем

схематичный рисунок шахматной доски.

ПП 2.2.

0,(7)

№29

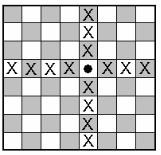
Пусть ладья занимает произвольное поле шахматной

доски. “Битых” полей (отмеченных крестиками) 7 по

горизонтали и 7 по вертикали, то есть всего 14. При

этом на доске всего 63 свободных поля, из которых

63-14=49

- “небитых”. P (A)=

N (A)

=

49

=

7

=0,(7).

N (Ω)

63 9

Какова вероятность того, что дни рождения 10 чело-

ПП 2.2.

век различны?

РЕШЕНИЕ:

0,883

№30

365(365 −1)...(365 −9)

1

9

P =

= 1 −

... 1

−

≈0,883 .

10

365

365

365

ПП 2.2.

Найдите вероятность того, что дни рождения 12 че-

-5

№31

ловек придутся на разные месяцы года.

3,9 10

РЕШЕНИЕ:

17

P(A) =

N( A)

=12 11 10 ... 1

=

12!

= 3,9 10-5.

N(Ω)

12 12

... 12

12

12

12 раз

Среди n лотерейных билетов k выигрышных. Нау-

дачу взяли m билетов. Найдите формулу для вычис-

ления вероятности того, что среди них l выигрыш-

ных. Определите вероятность того, что среди 10 би-

летов 1 выигрышный, если n =100 , k =10 ,

m =10 .

РЕШЕНИЕ:

Число способов выбрать m билетов из n равно Cnm ,

l

m−l

ПП 2.2.

число способов выбрать l

выигрышных билетов из

Сk Cn−k

,

m

№32

k равно Ckl , число способов выбрать m −l невыиг-

Cn

0, 408

рышных билетов из n −l равно Cnm−−kl , что дает

P(A) =

N (A)

Сl

Cm−l

=

k n−k

.

N(Ω)

Cm

n

P(A) =

С1

C9

≈ 0,408 .

10

10 90

C

100

В лотерее n билетов, из которых k выигрывают.

Участник лотереи покупает m билетов. Найдите

формулу для вычисления вероятности того, что хотя

бы один билет выиграет. Определите вероятность то-

го, что среди 10 билетов хотя бы 1 выигрышный, ес-

ли n =100 , k =10 , m =10 .

k

ПП 2.2.

РЕШЕНИЕ:

1−

Cn-m

,

k

Cn

№33

Событие A {не выиграет ни один билет} противопо-

≈ 0,67

ложно событию A {хотя бы один билет выиграет}.

N(

)

С0

Cm

Cm

Cm

A

P(A) =

P(A) =1−

=

k

m n−k =

n−k

,

n−k

.

N(Ω)

C

m

m

n

C

C

n

n

P(A) =1−

C10

≈ 0,67 .

90

10

C

100

Имеются изделия четырех сортов, причем число из-

делий i-го сорта равно соответственно

ni (i = 1, 2, 3, 4). Для контроля наудачу берутся т из-

делий. Найдите формулу для вычисления вероятно-

ПП 2.2.

сти того, что среди них т1 – первосортных, т2, т3 и

0,063

№34

т4 – второго, третьего и четвертого сорта соответст-

венно. Определите вероятность этого, если n1 = 2,

n2 = 3, n3 = 1, n4 = 3; m1 = 2, m2 = 1, m3 = 0, m4 = 2.

РЕШЕНИЕ:

Событие А {среди взятых для контроля т изделий т1

– первосортных, т2, т3 и т4 – второго, третьего и

18

четвертого сорта соответственно}.

m = m1 + m2 + m3 + m4 – число изделий, взятых для

контроля;

n = n1 + n2 + n3 + n4 – общее количество изделий.

Число способов взять т изделий из п равно

N(Ω) = Cnm .

Количества способов выбрать для контроля m1 изде-

лий первого, m1 второго и т.д. сорта из имеющихся

равны соответственно

Cnm1

,

Cnm2 ,

Cnm3 ,

Cnm4 .

Тогда

1

2

3

4

N(A) = Cnm1 Cnm2 Cnm3 Cnm4

,

1

2

3

4

m

m

m

m

P(A) =

N (A)

Cn11 Cn22 Cn33 Cn44

=

.

Cnm

N (Ω)

Если n1 = 2, n2 = 3, n3 = 1, n4 = 3;

m1 = 2, m2 = 1, m3

= 0, m4 = 2, то

C2

C1

C0 C2

9

P(A) =

=

= 0,063.

2

3

1

3

C5

126

9

32 карты распределяются между тремя игроками по

10 карт, две – «в прикупе». Какова вероятность того,

что в прикупе окажутся два туза?

РЕШЕНИЕ:

ПП 2.2.

Число комбинаций по две карты из 32, которые

0,012

№35

могут быть в прикупе N(Ω) = C322 .

Так как в колоде 4 туза, число комбинаций, дающих

2 туза, равно N(A) =C42 .

P(A) =

N (A)

C42

4!

2! 30!

6

= 0,012.

=

=

=

C322

2!2!

32

496

N (Ω)

Среди 25 экзаменационных билетов 5 «хороших».

Два студента по очереди берут по одному билету.

Найдите вероятности событий:

а) А – первый взял «хороший» билет;

б) В – оба взяли «хорошие» билеты.

ПП 2.2.

РЕШЕНИЕ:

0,2;

Общее число исходов опыта равно числу возможно-

№36

стей взять последовательно два билета из 25:

0,0(3)

N(Ω) = A252

= 25 ·24.

Число способов, которыми могут осуществиться со-

бытия А и В, соответственно равны

N(A) = C51 · C241

и N(B) = A52 .

19

P(A) =

N (A)

=

C1

C1

=

5 24

=

1

=0,2 ;

5

24

N (Ω)

A252

25 24

5

P(B) =

N (B)

A52

5 4

1

= 0,0(3).

=

=

=

N (Ω)

A252

25 24

30

В лифт k-этажного дома сели п пассажиров (п<k). Каждый может выйти на любом, начиная со второго, этаже. Найдите формулу для вычисления вероятности событий:

1)А {все вышли на разных этажах};

2)В {по крайней мере двое вышли на втором этаже}. Определите вероятность этих событий, если в доме семь этажей, а пассажиров – трое.

РЕШЕНИЕ:

Так как каждый может выйти на любом из (k – 1)

	этаже, то полное число элементарных исходов опыта	0,(5);
ПП 2.2.	равно N(Ω) = (k – 1)n.
№37	1) Число благоприятных исходов, соответствующих	0,(4)

событию А, равно N(A) =

An

k −l .

N (A)

=

An

P(A) = N (Ω)

(k −1)n .

k −1

2) Вероятность события В найдем, воспользовавшись

тем, что события А и В являются противоположными

Р(В)=1 – P(A)=1−

An

(k −

1)n .

k

-1

Если k = 7 и п = 3, то

5

4

6 5 4

5

=0,(4).

P (A) = 6 6 6

= 9 = 0,(5),

P(B)

= 1−

=

9

9

В результате бросания 12 игральных костей каждая

грань появилась дважды. Является ли редким такое

событие?

РЕШЕНИЕ:

В этом опыте возможно N(Ω) = 612 различных равно-

ПП 2.2.

вероятных исходов.

Интересующее нас событие осуществляется столь-

да

№38

кими способами, сколькими 12 костей можно раз-

бить на 6 групп по 2 в каждой:

N (A) = C12 (2, 2, 2, 2, 2, 2).

P (A) =

N (A)

C12 (2, 2 ,2, 2, 2, 2)

12!

= 0,003488.

=

= 612

N (Ω)

612

Таким образом, такой исход маловероятен.

ПП 2.2.

При игре в бридж 52 карты делятся на 4 разные

0,105,

№39

группы. Число различных раскладов равно

≈3, 46 10−9

20