praktice algem

2.2. Прямая в пространстве

Прямая в декартовой прямоугольной системе координат Oxyz может быть задана уравнением одного из следующих видов:

1). Общие уравнения

A1x + B1y + C1z + D1 = 0,A2x + B2 y + C2z + D2 = 0.

Прямая задана как линия пересечения двух плоскостей, где коэффициенты A1, B1,C1 не пропорциональны A2, B2,C2 .

2). Параметрические уравнения

x = x0 + pt,
	+qt,
y = y0
	+ rt,
z = z0

где M0 = (x0; y0; z0 ) - заданная точка прямой, l

= (p;q;r) - направляющий вектор

прямой.

3). Канонические уравнения прямой, проходящей

через точку

M0 (x0; y0; z0 )

параллельно вектору l = (p;q;r).

x − x0

=

y − y0

=

z − z0

.

p

q

r

4). Уравнение прямой, проходящей через две заданные точки

M1 (x1; y1; z1)

и

M2 (x2; y2; z2 )

x − x1

=

y − y1

=

z − z1

.

x

− x

y

− y

z

2

− z

2

1

2

1

1

Угол ϕ между прямыми

с

направляющими

векторами

= ( p1,q1,r1)

и

l1

l2 = ( p2,q2,r2 ) :

cosϕ =

			l1		l2
cos l ,l		=					.
1	2		l1			l2

Условие параллельности прямых:

l		l , или p1		= q1		= r1 .
1		2	p2		q2		r2

Условие перпендикулярности прямых:

		, или				= 0.
l1	l2		l1	l2	= p1 p2 + q1 q2 + r1 r2

Расстояние от точки M1 (x1, y1, z1) до прямой

			M	0		M	1	, l
d =											.
						l

x − x0 = y − y0 = z − z0 : p q r

21

Пример 1. Привести уравнения прямой к каноническому виду:

2x − y + 3z −1 = ,5 + 4 − − 7 = .x y z

Решение.
1 способ. Нормальные векторы плоскостей										2x − y + 3z −1 = 0	и 5x + 4y − z − 7 = 0
1 = (2;−1;3)	и	2	= (5;4;			−1)	соответственно. Эти векторы				перпендикулярны
направляющему вектору l							прямой. Поэтому
					i	j	k
l	= 1	× 2	=		2 −1 3			= −11i	+17 j +13k .
					5	4	−1

В качестве точки M0 (x0 , y0 , z0 ), через которую проходит

искомая прямая, можно взять, например, точку её пересечения с координатной плоскостью Оху:

z0 =	,	2x0 − y0 −1 = ,
			+ 4y0	− 7 = ,
		5x0

откуда x0 =11/13,	y0 = 9/13,			M0 (11/13,9/13,0).
Зная точку M0	и направляющий вектор l , запишем
канонические уравнения прямой									Рис.18
		x −11/13 = y −9/13					= z − 0 .
		−11			17			13

2 способ. Исключив из системы уравнений сначала y, потом x, получим систему

13x +11z −11 =

,

−13y +17z + 9 = .

Разрешим каждое уравнение относительно z:

z =

13(x −11/13)

=

13(y − 9/13)

, или

x −11/13

=

y −9/13

=

z

.

−11

−11

17

17

13

Пример 2. Определить, при каком условии прямые

x − x1

=

y − y1

=

z − z1

и

x − x2

=

y − y2

=

z − z2

p

r

p

q

1

q

2

r

2

1

1

2

компланарны, т.е. лежат в одной плоскости.

Решение. Данные прямые находятся в одной

плоскости только при условии, что векторы

( p1;q1;r1) и

M1M2 = (x2 − x1 , y2 − y1 , z2 − z1 ), l1 =

компланарны, т.е. смешанное

l2 = ( p2;q2;r2 )

Рис. 19

произведение этих векторов равно нулю:

x2 − x1

y2 − y1 z2 − z1

(M1M2, l1, l2 )= 0

, или

p1

q1

r1

= 0 .

p2

q2

r2

22

Пример 3. В уравнениях прямой

x

=

y

=

z

определить параметр а так, чтобы

2

− 3

a

эта прямая пересекаласьспрямой

x +1

=

y + 5

=

z

, и найти точку их пересечения.

3

2

1

= (2,−3, a)

= (3,2,1) не являются

Решение. Направляющие векторы прямых l1

и l2

коллинеарными, так как 2

≠ −

3

.

Следовательно,

эти

прямые не будут

3

2

параллельными при любом значении а.

Запишем условие компланарности прямых (см. пример 2):

−1− 0 − 5 − 0 0 − 0

, откуда а = 1.

2

− 3

а

=

3

2

1

Координаты точки

M0 (x0 , y0 , z0 )

пересечения

прямых есть

решение

системы, составленной из уравнений этих прямых:

x

0

=

y

0

=

z

0

,

2

− 3

1

+1

y0

+ 5

z0

x0

=

=

,

3

2

1

Из первого равенства

выразим

x0

= 2z0 ,

y0

= −3z0 и

подставим во

второе, в

результате получим x0

= 2, y0 = −3, z0

= 1, или M0 (2,−3,1).

Пример 4. Составить уравнения прямой, проходящей через точку A(3;2;4) и пересекающей ось Oy под прямым углом.

Решение. Искомая прямая перпендикулярна оси Oy и пересекает её, следовательно, проходит через точку B( ;2;0) (рис.20). Составим уравнение прямой, проходящей через две заданные точки

x − 3

=

y − 2

=

z − 4

, или

x − 3

=

y − 2

=

z − 4

.

0 − 3

0

2 − 2 0 − 4

− 3

− 4

Пример 5. Выяснить взаимное расположение прямых

x

=

y −1

=

z + 2

и

x +1

=

y +1

=

z − 2

.

2

0

−1

1

2

−1

y

Вычислить угол ϕ между ними.

Решение. Проверим условие компланарности, т.е. лежат ли прямые в одной плоскости (см. пример 2):

	−1− 0 −1−1 2 − (− 2)			Рис.20
	2	0	−1 = 12 ≠ 0 .

12 −1

Прямые не лежат в одной плоскости, то есть скрещиваются. Найдем угол ϕ между прямыми:

		21+ 0 2 −1(−1)						3					3	0
cosϕ =						=				,	откуда ϕ = arccos				≈ 57 .
													30
		(− 2)2 + 02 +12		12 + 22 + (−1)2				30

23

	Примеры для самостоятельного решения
1.	Составить уравнение прямой, проходящей через точку							M (1;1;1)					и
перпендикулярной векторам 1 = 2i + 3 j + k и 2 = 3i + j + 2k .
	Ответ:				x −1	=		y −1			=	z −1			.
					5			−1
												− 7
2.	Вычислить углы, образованные с осями координат прямой x − 2y − 5 =										,
				x − 3z + 8 = .
	Ответ: cosα =	6	;cos β =					3	;cosγ =				2	.
							7						7
	7

3. Найти уравнения прямой, проходящей через точку A(1;−2;3) и образующей с осями Ox и Oy углы 450 и 600 соответственно.

Ответ:

x −

1

=

y + 2

=

z − 3

.

2

1

±1

4. Даны три последовательные вершины

параллелограмма

ABCD : A(3; ;−1),

B(1;2;−4) и C( ;7;−2). Найти уравнения сторон AD и СD .

Ответ:

x − 3

=

y

=

z +1

;

x

=

y − 7

=

z + 2

.

− 2

−1

5

2

2

3

5. Вычислить

расстояние

между

параллельными

прямыми

x

=

y − 3

=

z − 2

и

1

2

1

x − 3

=

y +1

=

z − 2

.

Ответ:

5 30

.

1

2

1

6

6. Найти угол ϕ между прямыми

4x − y − z +12 = ,

и 3x − 2y +16 =

,

y − z − 2 = .

3x − z = .

Ответ: cosϕ =

20

.

21

2.3. Прямая и плоскость

Угол между прямой

x − x0

=

y − y0

=

z − z0

с направляющим вектором l = ( p,q,r)

p

q

r

и плоскостью Ax + By + Cz + D = 0 с нормальным вектором = (A,B,C) :

sinϕ =

l

=

Ap + Bq + Cr

.

l

A2 + B2 + C2 p2 + q2 + r2

Условие параллельности прямой и плоскости

l , или Ap + Bq + Cr = 0 .

Условие перпендикулярности прямой и плоскости

|| l , или

A

=

B

=

C

p

q

r

Пример

1.

При каких

значениях

α

и

β

прямая

x −1

=

y +1

=

z − 3

α

4

− 2

перпендикулярна к плоскости 3x + 2y − β z + 2 = 0?

24

Решение.

Прямая

перпендикулярна

к

плоскости, если ее направляющий вектор

l

коллинеарен

нормальному вектору

плоскости

(рис.21):

l

, или в координатах

α

=

4

=

−2

, откуда α = 6, β =1.

3

2

−β

Пример

2.

Найти точку B , симметричную

Рис.21

точке

A(1;1;1)

относительно

плоскости

x + y − 2 z − 6 = 0 .

Решение. Составим канонические уравнения прямой A на заданную плоскость (т.е прямой, проходящей через точку перпендикулярно плоскости). Эта прямая проходит через

точку A(1;1;1) параллельно вектору = (1;1;−2), поэтому ее уравнение имеет вид:

AB , проецирующей точку

x − 1

=

y − 1

=

z − 1

.

1

1

− 2

Определим

координаты

точки

A0

Рис. 22

пересечения прямой и плоскости (проекции

точки A на заданную плоскость),

решая

совместно

уравнения

прямой и

плоскости:

x −1

y

0

−1

z

0

−1

0

=

=

,

откуда A0 (2;2;−1).

1

1

−2

x + y

0

− 2z

0

− 6 = 0,

0

A ─ середина отрезка

AB , следовательно,

x =

xA + xB

, y =

yA + yB

, z

0

=

zA + zB

,

0

0

2

0

2

2

1+ xB

1+ yB

1+ zB

т.е. 2 =

,2 =

,−1=

,

откуда B(3;3;−3).

2

2

2

Пример 3. Исследовать взаимное

расположение прямой

x − x0

=

y − y0

=

z − z0

и

p

q

r

плоскости Ax + By + Cz + D = 0.

	Решение.
	Случай 1. (Рис. 23) Прямая пересекает
	плоскость при условии, что вектор l = ( p, q, r)
	не перпендикулярен вектору = ( A, B,C) или в
	координатной форме Ap + Bq + Cr ≠ 0 .	Рис. 23
	Случай 2. Прямая и плоскость параллельны
	(рис. 24), если они не имеют общих точек, в
	том числе M0 (x0 ; y0 ; z0 ) не принадлежит плоскости, и l .

25

		В координатной форме	Ap + Bq + Cr = 0,
			{Ax + By + Cz			+ D ≠ 0.
			0	0	0
Случай 3. Прямая лежит в плоскости			(рис.25),	если		M0 принадлежит этой
плоскости и					= ,
	l	. В координатной форме: Ap + Bq + Cr
			Ax0 + By0 + Cz0 + D = .

Рис. 24

Рис. 25

Пример 4.	Выяснить взаимное	расположение прямой		x −1		=	y +1		=	z	и
				1			2
									3
плоскости	x + y + 2z − 5 = 0 . Найти	уравнение плоскости,	проходящей						через
заданную прямую перпендикулярно заданной плоскости.

Решение. Прямая проходит через точку , её направляющий вектор

l = (1;2;3).

Нормальный

вектор

плоскости

= (1;1;2).

Так как

=1 1+ 2 1

+ 3 2 ≠ 0 ,

l

следовательно, прямая пересекает плоскость.

Точка

M (x, y, z)

принадлежит

плоскости,

проходящей

через

прямую

x −1

=

y +1

=

z

1

2

3

M (x, y, z)

перпендикулярно

плоскости

x + y + 2z − 5 = 0 ,

только при условии, что векторы

M0 M ,

и l

M0 (1;−1;0)

компланарны:

x −1 y − (−1) z − 0

= 0,

1

1

2

1

2

3

откуда уравнение искомой плоскости x + y − z = 0 . Пример 5. Определить углы, которые образует

прямая	x + y − z −1= ,			с координатными
	3x + 3y − 2z	− 2	= 0

	плоскостями. Выяснить взаимное расположение	Рис. 26
	этой прямой и координатных плоскостей.

26

Решение. Определим направляющий

вектор прямой (см. 2.2, пример 1):

i

j

k

(здесь

и

–нормальные векторы плоскостей

l

= 1

× 2

=

1

1

−1

= i

− j

1

2

3

3

−2

x + y − z − 1 = 0 , 2x + 3y − 2z − 2 = 0).

Угол между прямой и плоскостью определяется углом между направляющим

вектором прямой и нормальным вектором плоскости. Пусть ϕ1 ,ϕ2 ,ϕ3

– углы,

которые образует данная прямая с плоскостями Oxy,Oxz,Oyz , тогда:

sinϕ =

10 + (−1) 0 + 0

1

= 0 ,

1

12 + (−1)2 + 02 1

sinϕ2 =

1 0 + (−1)1+ 0 0

=

− 2

,

l

2

12 + (−1)2 + 02 1

1 1+ (−1) 0 + 0 0

k

2

, откуда

sinϕ

3

= cos l, i

=

=

12 + (−1)2 + 02 1

2

π

, ϕ3 =

π

i

j

ϕ1 = 0, ϕ2 = 4

4 .

Т.к.

ϕ2 ≠ 0, ϕ3 ≠ 0,

то

прямая

пересекает

плоскости

Oxz,Oyz . Т.к.

ϕ1 = 0 ,

то

прямая

Рис. 27

параллельна плоскости Oxy или лежит в этой

плоскости.

Найдем координаты какой-либо точки

M0 (x0 ; y0 ; z0 )

данной

прямой,

например,

точки

пересечения

с

плоскостью

Oxz .

Тогда

y0

= 0

и

x

0

− z

0

=1,

откуда x0 =

, z0

= −1. Т.к. z0 ≠ 0 , то M

0 Oxy , следовательно, прямая

3x0 − 2z0 = 2,

не лежит в плоскости Oxy , а только параллельна этой плоскости (рис.27).

Примеры для самостоятельного решения

1. Определить угол между прямой x + y + z − 2 =

,

и плоскостью, проходящей

2x − y + z − 2 = 0

через точки A(2;3;−1), B(1;1;0) и C(

;−2;1).

1

Ответ: arcsin

.

2

7

2. Написать уравнения проекций прямой x + 2y − 3z +1 =

, на координатные

x − y + z − 2 = 0

плоскости.

Ответ:

− 4x + y + 5 = ,

3x − z − 3 = , − 3y + 4z − 3 = ,

z

= ;

y = ;

x = .

3. Найти

точку

B , симметричную

точке A(1; 1; 1)

относительно

прямой

x −1

y

z +1

9

4

22

=

=

.

Ответ: B

;−

;−

.

2

3

−1

7

7

7

27

4. Написать уравнение плоскости, проходящей через прямую x2+1 = y−−11 = z −3 2

параллельно прямой

x

=

y + 2

=

z − 3

.

Ответ: x − y − z + 4 = 0 .

−1

2

− 3

5. Определить, при

каком

значении

λ

плоскость

5x − 3y + λz +1 = 0 будет

параллельна прямой x − 4z −1 = ,

Ответ:

y − 3z + 2 = .

λ = −11.

6. Определить, при

каких

значениях

A

и B

плоскость

Ax + By + 3z − 5 = 0

x = 3 + 2t,

перпендикулярна прямой y = 5 − 3t,

Ответ:

z = 2 − 2t.

A = −3, B =

9

.

2

7. Выяснить расположение

прямой

3x − 2y + 3z − 6 =

, по

отношению к

x − y + z − 2 = 0

координатным плоскостям.

Ответ:

пересекает

Oxy,Oyz ;

принадлежит Oxz

2.4. Прямая на плоскости

Прямая на плоскости в декартовой прямоугольной системе координат Oxy может быть задана уравнением одного из следующих видов:

1)	Ax + By + C = 0 – общее уравнение прямой;
2)	A(x − x0 )+ B(y − y0 )= 0 ─ уравнение прямой, проходящей						через				точку
M 0 (x0 ; y0 )			перпендикулярно нормальному вектору = (A;B);
3)	x − x0	=		y − y0	– каноническое уравнение прямой, где M		(x	; y		)	– точка
						0			0
	p			q			0

прямой, l = (p;q)– направляющий вектор прямой;

4)x = x0 + pt, (− ∞;+∞).– прямой

t параметрические уравнения ;

y = y0 + qt,

5)x + y = 1– уравнение прямой в отрезках; a b

6)y = kx + b – уравнение прямой с угловым коэффициентом k = tgα , где α –

угол, который составляет прямая с положительным направлением оси Ox ;
7)	x − x1	=	y − y1		─ уравнение прямой, проходящей через две точки M	1	(x ; y )
	x2 − x1		y2 − y1				1	1
и M2 (x2; y2 );
8)	y − y0	= k(x − x0 )			─ уравнение прямой с угловым коэффициентом			k ,
проходящей через точку M 0 (x0 ; y0 ).

Угол ϕ между прямыми на плоскости

28

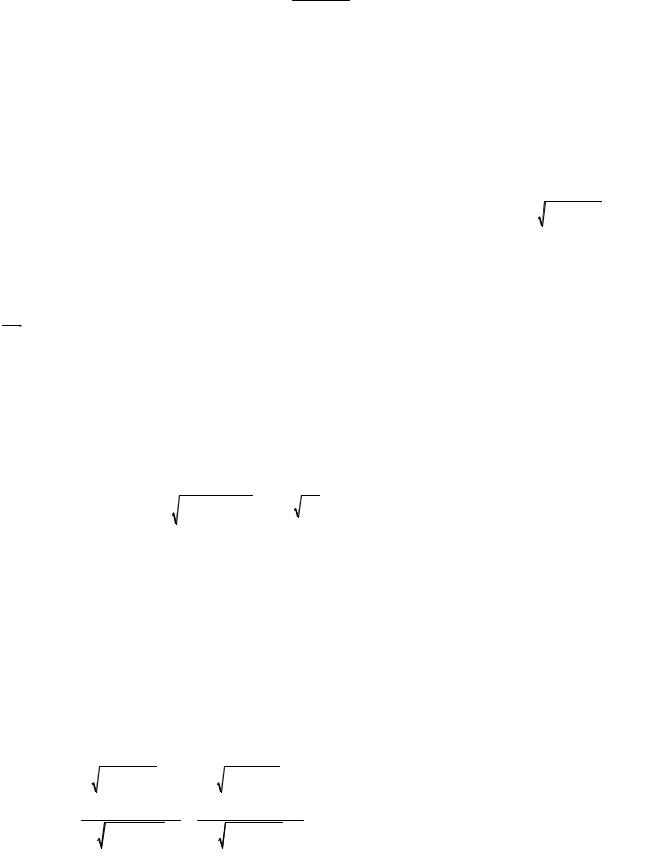
k

− k

2

2

cosϕ = cos( 1, 2 )

1

, или tgϕ =

1

,

=

1

+ k1k2

2

1

- нормальные векторыпрямых, k1 , k2

где 1

, 2

- угловые коэффициенты прямых.

Условие параллельности прямых

A

B

k

= k

2

, или

||

2

1

=

1

.

1

1

A2

B2

Условие перпендикулярности прямых

k1 k2 = −1 , или

A1A2 + B1B2 = 0 .

1 2 = 0

Расстояние от точки M 0 (x0 ; y0 )

до прямой Ax + By + C =

0 :

d =

Ax0

+ By0 + C

.

A2 + B2

Пример 1. Составить уравнение высоты треугольника ABC , проведенной из точки C , и определить её длину, если A( ;1), B(6;5), C(12;−1).

Решение. Уравнение	высоты CH треугольника ABC (рис.28) составим как
уравнение прямой, проходящей через точку C(12;−1) с нормальным вектором
AB = (6 − ;5 −1) = (6;4):	6(x −12)+ 4(y +1) = 0 , или 3x + 2y − 34 = 0 .

Длину высоты CH находим как расстояние от точки C до прямой AB . Уравнение AB

составим по точкам A( ;1) и B(6;5):

x − 0

=

y −1

, или 2x − 3y + 3 = 0 .

6 − 0

5 −1

Тогда

CH

=

2 12 − 3 (−1)+ 3

=

30

.

22 + (−3)2

13

Пример 2. Составить уравнения биссектрис

углов между прямыми	A1x + B1y + C1 = 0 и
A2x + B2 y + C2 = 0 .

Решение. Биссектриса угла – множество точек, равноудалённых от его сторон, то есть в данном случае, от прямых A1x + B1y + C1 = 0 и

A2x + B2 y + C2 = 0 .

Точка M (x; y) принадлежит биссектрисе тогда и только тогда, когда

A1x + B1y + C1

=

A2x

+ B2 y +

C2

, или

A2

+ B 2

A2

+ B2

1

1

2

2

A1x + B1y + C1 ± A2x + B2 y + C2 = 0 .

A2	+ B 2	A2	+ B2
1	1	2	2

Это и есть уравнения обеих биссектрис. Пример 3. Составить уравнение прямой,

Рис. 28

Рис.29

29

проходящей через точку M(5;1) и образующей с прямой 2x + y − 4 = 0 угол π4 .

Решение. Угловой коэффициент данной прямой 2x + y − 4 = 0 равен –2. Тогда угловой коэффициент k искомой прямой должен удовлетворять условию

		k + 2		= tg			π	,
		1− 2k					4
	откуда, учитывая равенство tg								π	= 1, получаем
									4
		k = 3,								Рис. 30
					1
		k = −				.
					3

Таким образом, условию задачи удовлетворяют две прямые.

Составим уравнения этих прямых по угловому коэффициенту и точке M :

	y −1 = 3(x − 5),			3x − y −14 = ,
		1	(x − 5),	или
	y −1 = −
				x + 3y − 8	= .
		3

Пример 4. Написать уравнение прямой, проходящей через точку P(2;4) на расстоянии 1 от точки Q( ;3).

Решение. 1 способ. Пусть Ax + By + C = 0 - общее уравнение искомой прямой. Координаты точки P удовлетворяют этому уравнению: 2A + 4B + C = 0 . Расстояние от точки Q до прямой равно 1:

0 A+ 3 B + C

=1 , или (3B + C)2 = A2 + B2 .

A2 + B2

2A + 4B + C = 0,

Для этого из

Решаем систему

2

= A

2

2

.

(3B + C)

+ B

первого уравнения выразим 3B + C = −2A − B и

подставим во второе. Возведем полученное уравнение

Рис. 31

в квадрат: 3A2 + 4AB = 0 и, учитывая первое уравнение,

получим

A = ,

C = −4B;

3

A,

C = A.

B = −

4

By − 4B =

,

y − 4 = 0,

Условию задачи удовлетворяют две прямые

3

или

4x − 3y + 4 = 0.

Ax −

Ay

+ A = ,

4

2 способ. Рассмотрим прямоугольный треугольник PQQ1 , где Q1 - проекция точки Q на искомую прямую.

QQ1 = 1по условию, PQ = (0 − 2)2 + (3− 4)2 = 5.

30