praktice algem

причем tgϕ =	y	, cosϕ =		x	, sinϕ =		y		.
	x			x2 + y2			x2 + y2

Тригонометрическая форма комплексного числа

z = z (cosϕ + i sinϕ ).

Показательная форма комплексного числа

z = z eiϕ .

Комплексное число z = x − i y - сопряженное комплексному числу z = x + i y . Операции над комплексными числами в алгебраической форме практически совпадают с операциями над линейными многочленами с учетом равенства

i 2 = −1.

Формула Муавра

zn = rn (cos nϕ + isin nϕ ), n .

Корни

степени

n

из

комплексного

числа

z = r (cosϕ + isinϕ)

–

вычисляются по формуле

ϕ + 2π k

ϕ + 2π k

, где k { ,1,...,n −1}.

ωk

= n

z

cos

+ i

sin

n

n

Пример 1. Доказать равенство z

=

z

2 ;

z

Решение. Пусть комплексное число z = x + i y . Тогда

= x − i y

z

z

= (x + i y) (x − i y) = x2 − i xy + i yx − (i y)2 = x2 −i2 y2 = x2 + y2 =

z

2 .

z

Пример

2.

Представить

число z

в алгебраической форме,

изобразить на

1

1

1− i

3

комплексной плоскости. Найти его модуль и аргумент: 1)

+

;

2)

.

− i

1+ i

1+ 4i

4

Решение.

1)

1

+

1

=

1

1− 4 i +

1

4 + i

=

1− 4i +

4 + i

= 1− 4i + 4 + i

=

5 − 3i

=

5

−

3

i .

4 − i

4 + i

1

+ 4i

1+ 4i

1− 4i

4 − i

1+16 16 +1

17

17

17 17

Число z получили в алгебраической форме. Изобразим его на комплексной плоскости (рис.51). Найдем модуль и аргумент комплексного числа:

2

2

5

3

34

3

z

=

+ −

=

, arg z = arctg −

.

17

17

17

5

2)

1−i 3

1−i

1−i

3

1− 2 i + i

2 3

1− 2 i + i

2 3

3

= i .

=

=

=

= (−i)

1+ i 1−i

1+1

2

1+ i

Из чертежа (рис.52) видно, что

z

=1, arg z =

π .

2

Пример 3. Решить систему линейных уравнений

(3−i)z +

(4+ 2i)z

2

=1+ 3i,

1

(4+ 2i)z

−(2+ 3i)z

2

= 7.

1

Решение.

Определитель системы

=

3 − i

4 + 2i

=

4 + 2i

− (2 + 3i)

= (3− i)(−(2 + 3i)) − (4 + 2i)(4 + 2i) = −6 − 9i + 2i + 3i2 −16 −16i − (2i)2 =

41

Рис. 51

Рис. 52

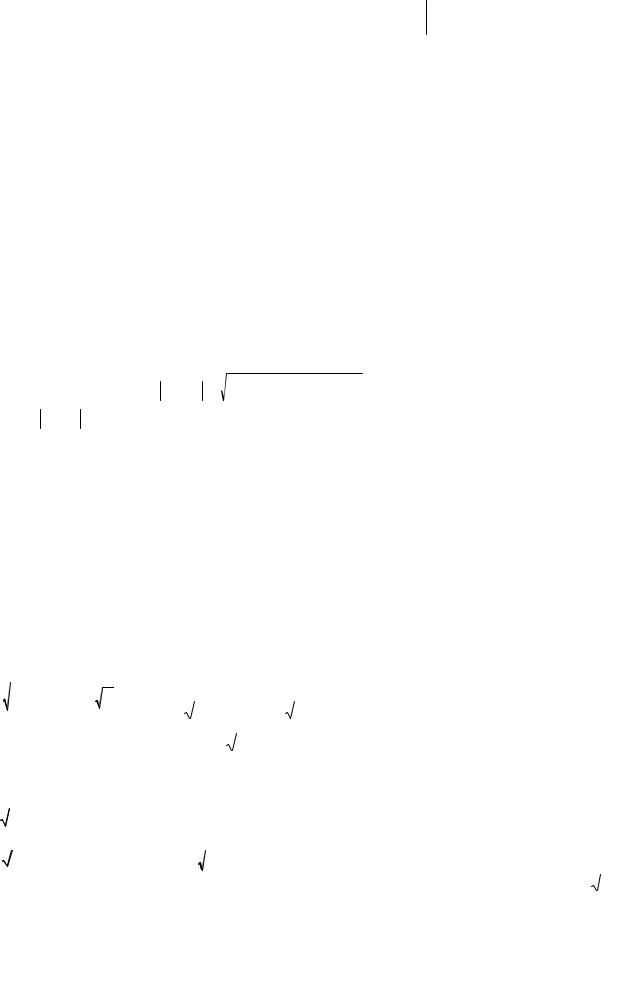
= −21− 23i ≠ 0 . Поэтому система имеет единственное решение, которое найдем методом Крамера. Вычислим определители:

1 =

1+ 3i

4 + 2i

= −21

− 23i ,

2 =

3− i

1+ 3i

7

−(

2 + 3i)

4 + 2i

7

Тогда z =

1 = −21− 23i

=1,

1

−21− 23i

z2

=

2 =

−23− 21i

=

i(−23i − 21)

= i .

−21− 23i

−21− 23i

Пример 4. Изобразить на комплексной плоскости

множество всех точек, удовлетворяющих условиям:

1) 0 ≤ Im z ≤ 3 ;

2)

z − z0

≤ R, где z0 C, R R- заданные числа ;

3)

z − i

=

z + 2

.

Решение.

1).

Так

как

Im z = y ,

то

заданное

неравенство

принимает

вид:

0 ≤ y ≤ 3, x R ,

и

определяет

горизонтальную полосу (рис.53). 2). Пусть z = x + iy , z0 = x0 + iy0 . Тогда

z − z0 = (x − x0 )+ i(y − y0 ), z − z0 = (x − x0 )2 + (y − y0 )2 . Условие z − z0 ≤ R может быть записано в виде

(x − x0 )2 + (y − y0 )2 ≤ R2 .

= −23− 21i .

Рис. 53

Рис. 54

Это соотношение определяет круг с центром в точке (x0 ; y0 ) радиуса R (рис.54).

3). Равенству

z −i

=

z + 2

удовлетворяют все точки z комплексной плоскости,

равноудаленные от точек z1

= i

и

z2 = −2, Эти

точки образуют серединный

перпендикуляр отрезка с концами z1 и z2

(рис.55).

Пример 5. Найти корни уравнений

1)ω4 = −1+ i , 2)ω2 = 3+ 4i .

Решение. 1). Комплексное число

z = −1+ i

представим

в тригонометрической форме. Для этого найдем его

модуль и аргумент:

1

1

3π

(−1)

2

+12 = 2

z

=

, sinϕ

=

, cosϕ

= −

ϕ =

.

4

2

2

3π

3π

Тригонометрическая форма: z =

2 cos

+ isin

.

4

4

Корни четвертой степени из z

(рис.56):

ωk

=

3π / 4 + 2π k

+ isin

3π / 4 + 2π k

k {0,1,2,3}

8 2

cos

,

4

4

ω

=

8

cos 3π + isin

3π , ω = 8

cos11π + isin 11π ,

0

2

2

1

16

16

16

16

8

2

42

Рис. 56

ω

= 8

cos19π

+ isin 19π ,

ω

= 8

cos 27π + isin 27π .

2

2

2

16

3

16

16

16

2). Представим комплексное число z = 3 + 4i

в виде полного квадрата:

3+ 4i = (4 −1) + 2 2 i = 22 + 2 2 i + i2 = (2 + i)2 = (−(2 + i))2 .

Тогда уравнению ω2 = 3+ 4i

удовлетворяют два комплексных числа ω1 = 2 + i ,

ω2

= −2 − i

Примеры для самостоятельного решения

3. Выполнить

указанные

операции.

Результат

представить

в

тригонометрической и алгебраической формах.

1)

(1+ i) (3+ i) −

(1− i) (3− i) ; 2)

i 5 + 2

; 3) (2i −i 2 )2 + (1−3i)2 .

3− i

3+ i

i19 +1

Ответ: 1)

14

i ; 2)

1

+

3

i ; 3)−11− 2i .

2

5

2

4. Доказать равенства а) z +

= 2Re z ;

б) z −

= 2i Im z ; в)

(

)= z ; г)

=

z

;

z

z

z

z

д) z1 + z2 = z1 + z2 ; е) z1z2 = z1 z2 ; ж) z1 / z2 = z1 / z2 .

Указание. Представить комплексное число в алгебраической форме и воспользоваться равенством z = x − i y .

43

5. Решить системы линейных уравнений:

	(2 +i) z + (2−i) z		2	= 6,				iz + z				2	= i,
1)		1					2)		1
		+ 2i)z +(3− 2i)z				= 8;		i +1 z −								(	i −1 z	2	=		(	i +1 .
	(3				2			(	)				1				)						)
		1
													Ответ: 1)									z		= 2+i, z	2	= 2−i ; 2) z =1+ic, z =c, c R.
																						1				1				2
6. Изобразить			на				комплексной плоскости множество всех точек,
удовлетворяющих условию: 1)											Re z				≤ 5; 2)					z +1				= 2 ; 3)			z		≥1− Re z .

Ответ: 1) полоса − 5 ≤ x ≤ 5; 2) окружность, центр(−1;0), R = 2 ; 3) y2 ≥1− 2x . 7. Найти корни из комплексных чисел и изобразить их на комплексной плоскости: а) 5− 9 ; б) 3 2 3 + 2i .

4. Матрицы и определители

4.1. Действия с матрицами

Пример 1. Вычислить произведения матриц:

						3			−2 3 4							1			−3		2 2				5		6
			1)												, 2)
									−4		2 5						3		−4		1		1		2 5			.
						5											2		−5		3		1		3 2
Решение. 1). Пусть строки матрицы															A =	3		− 2			есть A , A , а столбцы матрицы
																	5	− 4							1		2
3	4	есть B , B			. Тогда по определению произведения матриц
B =				2
		1
2	5
			A B						A B					33+		(	−2	)	2		3 4 +			(	−2	)	5	= (5 2) .
		A B =			1		1		1		2	=
		A2 B1							A2 B2						53+ (−4) 2						5 4 + (				−4)5			7 0
									1 − 3 2							2 5				6
2). Аналогично, если						A =			3	− 4		1		,	B =		1	2		5		, то
									2 − 5 3								1 3			2

A1B1 AB = A2B1

A3B1

A1B2 A2B2 A3B2

A1B3					2−3+ 2	5−6+ 6 6−15+ 4		1	5	−5
A	2	B	3		= 6− 4+1	15−8+3 18− 20 + 2 = 3			10	0 .
		B				10−10+9 12− 25+ 6			9
A			3		4−5+3			2		−7
	3

Пример 2. Вычислить (32												−2−1)n .				−2)		= (3	−2)(	3 −2)= (6 −6			−3+ 4)= (0				1).
Решение. Вычислим сначала (3																	2
														2		−1		2	−1	2	−1	4 −3	−2 +	2		1 0
	(				)	3	(			)(			)	(			)			4
Тогда			2	−1					1	0	2	−1			2	−1		2	−1		2	−1 2	−1	1		0
						=							=
																		;		=				=			.
			3 −2						0 1 3 −2						3 −2			3	− 2		3	− 2 3	− 2		0	1
Таким образом, если n = 2k													(четное), то
2 −1		n		2		−1		2k		1	0
(3 −2)			= (3 −2)							= (0 1).
Если n = 2k +1 (нечетное), то (32																−−21)n = (32			−−21)2k+1		= (32	−−21) .

44

Пример 3. Найти матрицу D = AB + BTC , если

	1	0
	1	1		,	0		3	2 −1		,	1		−1 1	0
					B =						С =			.
A =	−1 1					1	0	−1 0				−1	1 1
														−1
	2	3

Решение.				Число			сток матрицы A равно числу столбцов матрицы B ,
следовательно,							произведение						AB		существует.					Вычислим			его.
	1		0						0		3	2	−1					0		1
	1		1		0	3	2	−1	1		3	1	−1		. Запишем B	T		3		0		. Число строк
AB =		−1	1		(1	0	−1	0 )=		1	−3	−3	1				=		2	−1
		2	3							3 6		1	−2						−1	0

матрицы BT	равно числу столбцов матрицы C , поэтому произведение BTС
					0		1									0 )=			−1		1				1		−1
существует и BTС = 3							0 (				1		−1		1				3		−3				3		0 .
						2	−1			−1 1					1 −1					3	−3 1 1
						−1	0													−1	1			−1			0
Матрицы AB и BTС одного размера, следовательно, их можно сложить
					0		3		2 −1						−1 1 1						−1				−1 4					3		−2
			T		1		3		1			−1			3		−3			3	0				4			0		4		−1
AB + B				C =		1	−3 −3 1							+		3 −3 1					1		=			4 −6 −2							2	.
						3	6		1 −2											−1	0					2 7				0		−2
															−1 1
Пример 4. Найти значение многочлена f (x) = 2x2 − x + 3																											от матрицы
															1			0		2
											A	=			− 1			1		0	.
															3			4		5
Решение. Запишем многочлен от матрицы																				f (A) = 2A2 − A+ 3E ,												E - единичная
матрица размера 3. Вычислим A2 = A A =																	1 0				2 1						0 2			7			8 12
																		−1		1	0	−1					1	0	=		−2		1		−2	.
																		3 4					3				4 5				14		24 31
																					5
Запишем f (A)				7			8 12					1			0 2				1		0 0
		= 2			−2		1		−2 −				−1		1	0		+ 30			1	0			=
					14		24 31						3		4 5						0 1
																			0
	14 16						24		−1 0							− 2			3		0 0					16 16					22
	=	− 4 2					− 4		+		1			−1 0			+			0	3 0				=		− 3 4				−	4	.
		28 48					62				− 3 − 4									0	0 3						25 44 60
																− 5
																																1		2
Пример 5. Найти все матрицы, перестановочные с матрицей A =																																			.
																																3		4
Решение. Матрицы A и B называются перестановочными, если AB = BA. Пусть
матрица B =	α			β	. Найдем произведения AB и BA .
	γ			δ
AB = (13 42) (αγ δβ )= (3αα++24γγ 3ββ++24δδ );																		BA = (αγ δβ )(13 42)= (αγ ++ 33δβ 22αγ ++ 44δβ ) .

Матрицы равны, если равны их соответствующие элементы. Получим систему с неизвестными α, β ,δ ,γ .

45

α + 2γ = α + 3β			2γ = 3β
β + 2δ = 2α + 4β			2δ = 2α + 3β
3α + 4γ = γ + 3δ			3δ = 3α	+ 3γ
			3β = 2γ
3β + 4δ = 2γ + 4δ

Так как последнее уравнение совпадает с первым, а второе будет пропорционально третьему, если 3β заменить на 2γ , то получим равносильную

систему: δ2γ==α3+βγ, .} Имеем два уравнения с четырьмя неизвестными. Выбрав два неизвестных (например α ,γ ) за параметры, выразим оставшиеся (β,δ ) через

					2
	них. Получим: β =	2	γ , δ = α + γ и матрица B =	α			γ	.
					3
		3
				γ	α + γ

Примеры для самостоятельного решения

1. Вычислить произведение матриц:

	2 −3				9			−6			1		3 0 3				2	1			0		0			6 −1
1)									; 2)			2	1	0		1	−1	1	.	Ответ: 1)					; 2)		7 3
		−6				6																0	0
	4							−4				0	−4	2		2	1	0									0 6
						1		0	1
2. Пусть											. Показать, что An = 2n−1 A.
			A =				0	0	0
							1	0	1

Указание. Вычислить A2 , применить метод математической индукции. 3. Справедливо ли равенство (A+ B)2 = A2 + 2AB + B2 ,

4

3 . − 4

	4		1	0			2		2	1
если						,						?	Ответ: нет.
	A =	1	1	1			B =	1	0	1
		0	1	0				1	1
										−1

4. Показать, что матрица	1		2		есть корень многочлена f (x) = x2 − 4x + 3 .
	A =
		0	3

		0		1	0
5. Найти общий вид матрицы	B третьего порядка, для которой		0	0	1		B = Ο .
			0	0	0

α		β	γ
					, α, β ,γ - произвольные числа.
Ответ: B =	0	0	0
	0	0	0

								4.2. Определители
Пример			1. Доказать,				что при действительных a,b,c корни уравнения
	a − x	b		= 0 действительны.
	b	c − x
Решение. Вычислим определитель
					a − x	b		= (a − x)(c − x)−b2	= x2 −(a + c)x −b2	+ ac .
					b c − x

46

Получим квадратное уравнение x2 − (a + c)x − b2 + ac = 0 . Корни этого уравнения действительны, если дискриминант неотрицателен. Вычислим дискриминант:

D = (a + c)2 + 4b2 + 4ac = a2 + 2ac + c2 + 4b2−4ac = a2 − 2ac + c2 + 4b 2= (a − c)2 + 4b2 ≥ 0

при любых действительных a,b,c .

Пример 2. Вычислить определитель																	2			0		5	по определению и используя
																	1			3		16
																	0			−1		10
свойства определителей
Решение. а). По определению
		2	0	5		= 2		3	16		− 0		1	16		+ 5			1	3		= 2 (30 +16)+ 5(−1) = 92 − 5 = 87 .
		1	3	16
		0	−1	10				−1	10				0	10					0	−1

б). Используя свойства: если вторую строку умножить на (− 2) и добавить к первой, определитель не изменит своего значения. Получим

2	0	5		=		0	−6	−27		= .
1	3	16				1	3	16
0	−1	10				0	−1	10

Раскроем определитель по элементам первого столбца (теорема разложения).

Тогда	= (−1)2+1	−6	−27	= −1 (−60 − 27) = 87 .
		−1	10
Пример 3. Вычислить определители
						0	1	1	1		3	−5	−2	2
			1)			1	0	1	1	, 2)	−4 7 4			4		.
						1	1	0	1		4	−9	−3	7
						1	1	1	0		2	−6	−3	2

Решение. Известно, что определитель, содержащий ниже (выше) главной диагонали нули, равен произведению элементов, стоящих на главной диагонали. Используя свойства определителей, приведем данные определители к виду, когда ниже главной диагонали стоят нули.

	0	1	1	1		3	1	1	1		1	1	1	1		1	1	1	1
1)	1	0	1	1	=	3	0	1	1	= 3	1	0	1	1	= 3	0	−1 0		0	= −3 .
	1	1	0	1		3	1	0	1		1	1	0	1		0	0	−1 0
	1	1	1	0		3	1	1	0		1	1	1	0		0	0	0	−1

Первоначально к первому столбцу добавили все остальные, затем из первого столбца вынесли общий множитель 3, и, наконец, последовательно вычли первую строку из всех остальных.

	3	−5	−2	2		−1 2		2	6		−1 2 2			6		−1	2	2	6
																0	−1 −4		−20
2)	−4 7		4 4		=	−4 7		4	4	=	0	−1 −4 −20			=					= 27.
	4	−9	−3	7		0	−2	1	11		0	−2	1	11		0	0	9	31
	2	−6	−3	2		2	−6	−3 2			0	−2	1	14		0	0	0	3

Первоначально вторую строку добавили к первой и третьей; затем первую строку сначала умножили на (-4) и добавили ко второй, потом на 2 и добавили к четвертой, и, наконец, второю строку умножили на (-2) и добавили к третьей, а третью вычли из четвертой.

47

Примеры для самостоятельного решения
1. Решить неравенство		x	3x		<14.												Ответ: x (−1;7).
		4	2x
	3		x			− 4
2. Решить уравнение.	2		−1				3		= 0.							Ответ: x = −10; x = 2 .
	x +10		1				1
						1			0 −1 0						3 − 3 − 5 8
3. Вычислить определители: 1)						3			− 2	0	4		;	2)	− 3	2	4	− 6		.
						1	1			1	1				2	− 5	− 7	5
						− 6 6 −1 −11									− 4 3		5 − 6
																Ответ: 1) 5;					2) 18.
		4.3. Обратная матрица
																					1	2
Пример 1. Выяснить, существует ли обратная матрица для матрицы A =																						.
																					3
																						4

Если обратная матрица существует, найти её.

Решение. Матрица обратима, если её определитель не равен нулю. Вычислим

det A =	1	2	= 14 − 2 3 = −2 ≠ 0 A−1 - существует.
	3	4

Найдем матрицу из алгебраических дополнений:

A11 = (−1)1+1 4 = 4, A12 = (−1)1+2 3 = −3 , A21 = −2 , A21 =1.

	A−1		1			A
Известно, что		=				11
			det			A21
				A

A	T		1	T	−2			1
12		A−1 =		(4 −3)	= 3				1 .
A22			−2	−2 1				−
									2
					2

Как		проверить							результат?		По определению				обратной							матрицы A−1 A = E и
A A−1 = E . Проверим эти равенства:
−1			−2			1			1	2 1	0	−1	1	2		−2			1			1	0
A	A =					−			(3	4)= (0	1)= E и	A A	= (3	4)					−			= (0	1)= E .
							2													2
			2													2

Матрица A−1 найдена верно.

	1		1	1	1
Пример 2. Найти обратную матрицу для матрицы A =	1		2	3	4	.
		1	3	6	10
			4	10	20
	1

Решение. Найдем

A−1 , используя метод Гаусса. Запишем матрицу

(A | E) и с

помощью преобразований приведем её к виду (E | A−1 ).

1 1 1 1 | 1 0

0

0

A1

A1

1 1 1 1 | 1 0

0

0

B1

B1 − B2

− A1

1 2 3 4 | 0 1

0

0

= A2

~

A2

= 0 1 2 3 | −1 1

0

0

= B2

~

B2

=

1 3 6 10 | 0 0

1

0

A

A

3

− A

2

0 1 3 6 | 0 −1

1

0

B

B − B

3

3

3

2

− A

1 4 10 20 | 0 0

0

1

A4

A

3

0 1 4 10 | 0 0

−1 1

B4

B4

− B3

4

48

1	0	−1 −2 | 2 −1					0 0						C1				C1 + C3									1 0 0 1 | 3												−3 1					0
0 1		2	3 | −1 1				0 0						C				C − 2C										0 1 0 −3 | −3											5 −2					0		=
=	0	1											=	2		~			2				3			=												−2 1
0			3 | 1 −2 1 0										C								C					0 0 1 3 | 1																	0
	0	1	4 | 0			1 −2 1								3							3						0 0 0 1 | −1											3 −3					1
0													C4					C4 − C3
D1		D1 − D4			1 0 0 0 | 4												−6				4			−1							4						−6	4			−1
D		D + 3D				0 1 0 0 | −6 14 −11 3																					A−1 =					−6 14						−11 3
= 2	~	2	4		=																												4 −11					10 −3					.
D		D − 3D			0 0 1 0 | 4											−11 10 −3
3		3	4			0 0 0 1 | −1 3															−3 1											−1 3						−3 1
D4			D4
																						1				2 −3						1 −3						0
Пример 3. Решить матричное уравнение																							3			2	−4										2	7
																												X =				10							.
																							2			−1 0												8
																																10 7
									1 2								− 3																				1	−3 0
Решение. Если матрица												3		2			− 4				обратима, то									X = A					−1				2		7
							A =																													10						.
												2 −1					0																					7			8
																																					10
Вычислим
	1	2	−3		(			(			)					(	)			(		))			(				(		)		(		)					)
det A = 3		2	−4 =		1 2 0 +		2		−4				2	+ 3			−1				−3			−		−3 2 2 +				−4				−1			1+	3 2 0			= −7 +8 =1.

2 −1 0

Так как det A ≠ 0 , то существует обратная матрица A−1 . Для её отыскания найдем алгебраические дополнения матрицы A :

A11 =	2 − 4				= −4, A12			=			3		− 4	(−1)3 = −8 , A13 =							3	2		(−1)4 = −7 , A21								= −		2 − 3						= 3,
	−1 0										2	0									2	−1											−1 0
		− 3																− 3									1	− 3								1	2
	1			= 6 , A = −					1		2		= 5,				2			= −2 , A = −										= −5 , A =									= −4 .
A =															A =
22	2	0				23			2		−1				31		2	− 4				32					3	− 4				33				3	2
							1			A11			A12		A13	T								− 4 3						− 2
По формуле					A−1	=				A21			A22		A23			получим				A−1 =			− 8			6		− 5	.
							det A				A		A		A										− 7			5		− 4
											31		32		33

	−4		3	−2 1			−3 0			6		4	5
Тогда		−8	6	−5			2	7			2	1	2
	X =					10				=				.
		−7	5	−4			7	8			3	3	3
					10

Пример 4. Показать, что матрица, обратная к неособенной симметричной матрице, будет симметричной.

Решение. Матрица называется симметричной, если для неё выполняется равенство AT = A. Пусть дана неособенная симметричная матрица A . Тогда det A ≠ 0 . Следовательно, для A существует обратная A−1 . Нужно показать, что

(A−1 )T = A−1 . Вспомним, что (A−1 )T = (AT )−1 и используем условие AT = A: (A−1)T = (AT )−1 = (A)−1 = A−1. Итак, (A−1 )T = A−1 , а это означает, что матрица A−1 - симметричная.

49

Примеры для самостоятельного решения

1. Найти, если возможно, обратную матрицу для матрицы

1		2	2																		1
A =	2	1	− 2	.											Ответ: A−1					=			A .
																					9
	2	− 2	1
2. Найти обратную матрицу для матрицы
1		1	1	1												−1			1	1			1
		−1
A = 1			1	1	.										Ответ: A−1 = 1	1			−1	0			0 .
1 1			−1 1												2			1 0 −1					0
																		1	0	0
		1	1																				−1
1				−1
						1		3 − 2			1 3		5			1		− 42 − 49					49
3.Решить уравнение						X	2	−1	1		=	0 2	− 4	.	Ответ: X =				22	16			−18	.
																7
							3	2	0			1 1	1						− 8	− 9			11

4. Пусть A и B - неособенные матрицы одного и того же порядка. Показать что, если AB = BA, то A−1B = BA−1 и A−1B−1 = B−1 A−1 .

4.4. Ранг матрицы

	1		3	5	−1
		2	−1	− 3	4
Пример 1. Вычислить ранг матрицы						.
	A =	5	1	−1	7
		7	7	9	1

Решение. С помощью элементарных преобразований приведем матрицу к ступенчатому виду.

1 3 5		−1		A1					A1					1 3				5 −1			B1				B1
	2 −1 −3	4		A			~	A − 2A							0		−7	−13 6			B				B		=
A =	5 1 −1	7		=	2				2		1		=		0		−14	−26 12			= 2		~		2
					A				A −	5A											B		B		− 2B
					3				3		1						−14	−26 8			3			3	2
	7 7 9	1			A4			A4 − 7A1							0						B4		B4 − 2B2
				1			3		5		−1				1		3	5	1
					0	−7			−13		6
				=										~		0 −7		−13 6		.
				0			0		0		0
																0 0		0	−4
					0		0		0		−4

Переставив третий и четвертый столбцы, получим матрицу ступенчатого вида

1		3	1	5
		− 7		−13		, поэтому rang A = 3.
A ~	0		6
	0	0	− 4	0

	1		λ	−1	2
Пример 2. Чему равен ранг матрицы				λ			при различных значениях
	A =	2	−1		5
		1	10	− 6	1

параметра λ ?

Решение. Приведем матрицу A к ступенчатому виду. Выполним следующие элементарные преобразования:

50