Ch_7_Integraly_po_figure

2. Свойство аддитивности. Пусть фигура Ф есть объединение двух фигур 1 и 2 , т.е. 1 2 , причём Ф1 Ф2 0 и функция f P интегрируема по1 и 2 . Тогда функция f P интегрируема по фигуре Ф и имеет место равен-

ство f P dμ f P dμ f P dμ .

1 2

Свойства, определяемые неравенствами (оценка интегралов по фигуре)

Пусть функция f P интегрируема по фигуре Ф. Тогда:
1.	Если для любой точки P Ф f P 0, то f P dμ 0 .
2.	Если для любой точки P Ф f P g P , то f P dμ g P dμ .

3.Если существуют такие два числа m, M, что для любой точки P Ф

m f P M , то mμ f P dμ Mμ , где μ мера Ф.

Свойство 3 для интегралов разных типов имеет вид:

b

1) m b a f x dx M b a .

a

2) mS f x, y dS MS .

D

3) mV f x, y, z dv MV .

G

4) mL f x, y, z dl ML .

L

5) mSпов f x, y, z dσ MSпов .

Теорема о среднем. Если функция f P непрерывна в замкнутой ограничен-

ной связной области Ф, то существует точка P , такая, что выполняется ра-

венство: f P dμ μf P .

Физический смысл теоремы о среднем. Пусть фигура Ф обладает массой, рас-

пределенной с плотностью	f P ρ P , тогда m f P dμ μf		. В случае
		P
			m Vρ		,
пространственной фигуры	мера фигуры равна объему μ V ,
				P

ρ P Vm – среднее значение плотности.

9

1.6. Геометрический смысл интегралов по фигуре

Пусть f P 1, тогда интеграл по фигуре будет равен мере соответст-

вующей фигуры, т. е. dμ μ . В частных случаях:

	b
1.	dx b a – длина отрезка Ox.
	a
2.	dS S – площадь области D.
	D
3.	dV V – объем пространственной области G.
	G
4.	dl L – длина линии L.
	L
5.	dσ S – площадь поверхности .

1.7. Механический смысл интегралов по фигуре

Пусть фигура Ф обладает массой, распределенной с плотностью f P ρ P , тогда масса фигуры выражается интегралом по фигуре

ρ P dμ m .

Ф

Двумерные и одномерные массивные объекты (поверхности и линии) возникают как модели трехмерных тел, у которых протяженность в одних направлениях существенно меньше протяженности в других.

2. ДВОЙНОЙ ИНТЕГРАЛ

Рассмотрим фигуру, которая является частью плоскости XOY: D . Интеграл по фигуре в данном случае является двойным интегралом от функции f(P)= f (x, y) по области D:

n

f (P)dS lim f (Pi ) Si .

D

rn 0 i 1

2.1. Геометрический смысл двойного интеграла

Задача (о вычислении объема тела)

Найдем объем тела, ограниченного сверху ку- сочно-гладкой поверхностью z f (x, y) 0, снизу

– частью плоскости XOY , принадлежащей ограни-

ченной замкнутой области D , а сбоку – цилиндрической поверхностью, образующие которой параллельны оси Oz, а направляющей является граница Г области D .

10

Разобьем

основание

D

на

конечное

число элементарных ячеек

S1, S2 ,..., Sn . В каждой

ячейке

выберем

точку

Mi (xi , yi ) Si

(i 1,2,...n) и построим столбик с осно-

ванием Si и высотой Mi Ni

f (xi , yi ) .

Если приближенно принять каждый столбик за

прямой цилиндр, то в этом приближении его объем ра-

вен Vi f (xi , yi ) Si , а объем всего тела приближен-

n

но равен V f (xi , yi ) Si . Перейдем к пределу

i 1

n

) S

f (x, y)dS

f (P)dS .

V lim f (x , y

i

r

0

i 1

i i

n

D

D

Вывод: если f (x, y) 0, то f (x, y)dS представляет объем криволинейного

D

цилиндра, построенного на области D и ограниченного сверху поверхностью f (x, y) .

Замечание. Если функция z f (x, y) в области D меняет знак, то в результате получится разность объёмов тел, одно из которых расположено выше плоскости XOY , а второе ниже. Таким образом, для произвольной функции

z f (x, y) интеграл f (x, y)dS может быть и отрицательным и равным нулю.

D

2.2. Вычисление двойного интеграла

Рассмотрим прямоугольную область интегрирования D {x [a,b]; y [c,d]}. Найдем объем тела, ограниченного кусочно-гладкой поверхностью z f (x, y) , плоскостью z 0 и цилиндрической поверхностью, образующие которой параллельны оси Oz, а направляющей служит граница области D .

Вычислим объем по площадям параллельных сечений.

Проведем плоскость x const (a x b). Фигура, получающаяся в сечении, представляет собой криволинейную трапецию, ограниченную линиями: z f (x, y) 0 (x const) , z 0 , y c , y d . Площадь сечения равна:

d

S(x) f (x, y)dy .

c

Объем всего тела равен

b

V S(x)dx

a

b d

f (x, y)dy dx .

a c

Ранее было показано, что объем такого тела равен двойному интегралу от f (x, y) по области D, таким образом:

11

	b d
f (x, y)dxdy f (x, y)dy dx .
D	a c
		d b

Аналогично: f (x, y)dxdy dy f (x, y)dx .

D c a

Замечание. Если функция z f (x, y) в прямоугольнике меняет знак, то вместо

d

площади поперечного сечения интеграл S(x) f (x, y)dy будет равен разности

	c
площадей криволинейных трапеций, расположенных выше и ниже оси
x const .
Замечание
b d

Запись двойного интеграла f (x, y)dxdy f (x, y)dy dx называют повтор-

D	a c
d		b
ным интегралом, при этом c	f (x, y)dy – называют внутренним, а a {...}dx

внешним интегралом.

Для того чтобы двойной интеграл мог быть вычислен как повторный, необходимо существование внутреннего интеграла при всех допустимых значениях внешней переменной.

Рассмотрим произвольную область интегрирования.

ОПРЕДЕЛЕНИЕ

Плоская двумерная область D, ограниченная простой замкнутой кусочногладкой плоской кривой называется правильной в направлении оси Ox или оси Oy , если любая прямая, пересекающая эту область и параллельная соответствующей координатной оси, пересекает границу области ровно в двух точках.

y

y

D

D

M

0

x

0

x

На левом рисунке область правильна в обоих направлениях, на правом рисунке область правильна в направлении оси Ox и неправильна в направлении оси Oy .

Замечание

Касаться области прямые, параллельные координатным осям, могут как в

одной точке, так и в бесконечном числе точек.	y
Последнее имеет место в случае, если часть гра-
ницы области параллельна одной из осей.	y 2 (x)

Теорема

Пусть D – правильная область в направлении Oy , ограниченная линиями

D

y 1 (x)

0

a

b

x

12

y φ1(x) , y φ2 (x) , x a , x b , и функция	f (x, y)	непрерывна в D . Тогда,
если при всех x a,b существует интеграл	φ2 ( x)
	J x	f (x, y)dy , то двойной

φ1 (x)

интеграл существует и равен

	f (x, y)dxdy	b φ2 ( x)
D		a φ1 (x)

f (x, y)dy dx .

Рассмотрение проводится аналогично предыдущему случаю; при этом площадь сечения вычисляется так:

			φ2 ( x)
		S(x)	f (x, y)dy ,
			φ1 (x)
а значение всего интеграла:	b	S(x)dx		b φ2 ( x)
					f (x, y)dy dx .
	a			a φ1 (x)

Таким образом,

	f (x, y)dxdy	b φ2 ( x)
			f (x, y)dy dx .
D		a φ1 (x)

Аналогично, если D – правильная область в направлении Ox , ограниченная

линиями x ψ1( y) ,	x ψ2 (y) ,		y c,	y d , то двойной интеграл равен
		f (x, y)dxdy		d ψ2 ( y )
					f (x, y)dx dy .
	D			c ψ1 ( y)

Правило вычисления двойных интегралов

1.Для того чтобы вычислить двойной интеграл по произвольной правильной области D , необходимо свести его к повторному (двукратному) интегралу и проинтегрировать функцию по одной из переменных в пределах, соответствующих произвольному, но неизменному значению другой переменной, а затем результат проинтегрировать в пределах ее полного изменения.

2.Если область D правильная в обоих направлениях, функция f (x, y) интегри-

руема в D и оба внутренних интеграла существуют, то порядок интегрирования может быть изменен в соответствии с равенствами

b φ2 ( x)

d ψ2 ( y )

f (x, y)dxdy dx

f (x, y)dy dy f (x, y)dx .

D

a φ1 (x)

c ψ1 ( y)

3. Если область D неправильная, то ее разбивают на конечное число непересекающихся правильных областей Di и двойной интеграл по области D вычисляют как сумму двойных интегралов по областям Di .

4. Внешний интеграл всегда вычисляется в постоянных пределах.

13

ПРИМЕР.				Вычислим					xy2dxdy ,										если								область											D задана неравенствами:
0 x 1, 2 y 3.									D
Решение:
	2			1			3	2	1				y3					3					1					27 8																35 x2										1					35 1 35
xy		dxdy xdx y							dy xdx														x													dx
												3																			3
D				0			2		0										2				0																					3 2										0					3 2 6
или
	2			3		2	1		3	2					x2							1	1					3			2							1 y3							3				1 35 35
xy			dxdy		y		dy xdx y				dy																	y				dy																																.
															2										2													2			3									2						3						6
D				2			0		2													0						2																	2
ПРИМЕР. Вычислим x2 ydxdy , где D – треугольник с																																																		y																B
									D																																			1
вершинами: O(0,0) , A(2,0), B(2,1) .
Решение:																																																																			A
																																	x															O														x 2							x
Область D , ограниченная прямыми																						y 0,						y						,		x 2,																								1
																																2																								x
является правильной. При фиксированном x																														y меняется от 0 до																											:
																																																								2
																			x 2																							2
				2			x 2		2				y		2									1		2									1 x				5							4
x2 ydxdy x2dx								ydy x2dx																		x4dx																					.
																																			8 5
OAB				0			0		0		2								0				8			0																0		5

ПРИМЕР. Изменим порядок интегрирования в повторном интеграле:

1 x

dx f (x, y)dy .

0 x2

Решение:

Область интегрирования D ограничена прямой y x и

параболой y x2 и является правильной как в отношении оси Ox, так и оси Oy с верхней границей y x и

нижней y x2 . Всякая прямая, параллельная оси Ox, пересекает границу области не более чем в двух точках, следовательно, можно вычислить интеграл, полагая внешние пределы интегрирования y 0, y 1. При

этом пределы во внутреннем интеграле будут иметь вид: нижний предел x1 y , верхний x2 y .

14

1	x	1	y
Таким образом: dx		f x,y dy dy		f x, y dx .
0	x2	0	y

ПРИМЕР. Расставим пределы интегрирования в двойном интеграле, если об-

x2 y2 1,

ласть D задана системой неравенств:

x2 y2 4.

Кольцо D – неправильная область. Разобьем ее на четыре правильных области:

... ... ... ... ... .

D

D1

D2

D3

D4

Границами правильных областей являются дуги соответствующих окружностей y 1 x2 , y 4 x2 и прямые x 1.

...

... ... ... ...

D

D1

D2

D3

D4

1

4 x2

1

4 x2

2

4 x2

1

1 x2

dx

... dy dx

... dy dx

... dy dx

... dy.

2

4 x2

1

1 x2

1

4 x2

1

4 x2

ПРИМЕР. Найдем площадь фигуры D , ограниченной параболами y x2 , y x .

Решение:

Полагаем f (x, y) 1;

			1	x	1
f (x, y)dS dS dxdy dx dy y							x2x dx
D	D	D	0	x2	0

1	1		1		3				1				1
		x2 dx			2	x					1	x3
	x		xdx x2dx
							2
					3
0	0		0						0	3			0

1 .

3

2.3.Замена переменных в двойном интеграле

Внекоторых случаях вычисление двойных интегралов значительно упрощается, если изменить область интегрирования, осуществив замену переменных в двойном интеграле.

Рассмотрим f (x, y)dxdy . Если координаты x и y являются функциями

D

новых переменных u и v :	x x(u,v),	то числа u и v называются криволи-
	y y(u,v),

нейными координатами точки M .

15

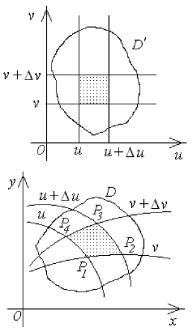
При этом область D на плоскости uOv отобразится в область D на плоскости xOy , и каждому значению f (x, y) в области D соответствует то же значение f (u,v) f (x(u,v), y(u,v)) в области D .

Потребуем, чтобы:

1)в пределах областей D и D соответствие между декартовыми и криволинейными координатами точки M было непрерывным и взаимно однозначным, т.е. различным точкам области D соответствовали различные точки области D ;

2)функции, осуществляющие прямое и обратное

x x(u,v),

отображения, т.е.

y y(u,v)

и	u u(x, y),	имели
	v v(x, y)

непрерывные первые частные производные в областях D и D соответственно;

		x		x
3) функциональный определитель J		u		v		не обращался в нуль.
		y		y
		u		v

Если отображение удовлетворяет указанным требованиям, то внутренние точки области D переходят во внутренние точки области D (и наоборот), а граничные точки переходят в граничные.

Замечание

u

u

x

x

x

y

Определители J

u

v

и J

называются якобианами

v

v

y

y

u

v

x

y

прямого и обратного преобразования соответственно.

на прямоугольные площадки приводит к разбиению

Разбиение области D

области D

на криволинейные четырехугольники с вершинами P1(x1, y1) ,

P2 (x2 , y2 ) ,

P3 (x3 , y3 ) ,

P4 (x4 , y4 ) ,

где

x1 x(u,v) ,

x2 x(u u,v) ,

x3 x(u u,v v) ,

x4 x(u,v v) ,

y1 y(u,v) ,

y2 y(u u,v) ,

y3 y(u u,v v), y4 y(u,v v) .

Заменяя приращения функций x(u, v) и y(u, v) соответствующими диффе-

	ренциалами по формуле f (u u, v v) f (u, v)	f	v	f	u , можно счи-
		v		u

16

тать,

что

x x(u,v) ,

x

2

x(u,v)

x

u ,

x x(u,v)

x

u

x

v ,

1

u

3

u

v

x

y

x x(u,v)

v ,

y y(u,v) ,

y y(x, y)

u ,

y y(u,v)

y

u

y

v ,

4

v

1

2

u

3

u

v

	y y(u,v)	y	v . Четырехугольник при этом можно рассматривать как парал-
		v
	4
	лелограмм. Его площадь

S

x

x

x x

(x x )(y y ) (x x )(y y )

[P P PP ]

2

1

4

1

1 2

1 4

y y

y y

2 1

4

1

4 1 2 1

2

1

4

1

x

y

x

y

x

y

x

y

x

x

u v

J

u v ,

u

v

v

u

u v

u

v

u

v

v

u

u v

v u

y

y

x

x

u

v

где J

u

v

− якобиан преобразования.

y

y

u v

Предельный переход для соответствующих интегральных сумм приводит к формуле преобразования координат в двойном интеграле:

f (x, y)dxdy f (x(u,v), y(u,v)) | J | dudv .

D D

ПРИМЕР. Вычислим (y x)dxdy , если об-

							D
ласть D задана уравнениями y x 1,
y x 3 , y	x			7		,	y	1	x 5.
3		3					3
Решение:									u y x,
										x
Сделаем замену переменных:
									v y		,
										3
тогда область D		будет задаваться прямыми:
u 1, u 3, v			7		,		v 5. Для вычисления яко-
		3

биана преобразования выразим x и y через u и v :

x	3	u	3	v ,	y	1	u	3	v .
4		4			4		4

17

x

x

3

3

9

3

3

При этом J

u

v

4

4

и (y x)dxdy

16

16

y

y

1

3

4

D

u

v

4

4

1

3

3

3

3

3

5

1

3

u

v

u

v

dudv

ududv

d

udu 8 .

4

4

4

4

4

D

4

4

D

7 3

3

2.4. Двойной интеграл в полярных координатах

Перейдем в полярную систему координат

x ρcosφ , y ρsin φ и вычис-

лим якобиан перехода. Если u φ ,

v ρ, x ρcosφ ,

y ρsin φ , то

x

x

cosφ

ρsin φ

J

ρ

φ

ρcos2 φ ρsin2 φ ρ

y

sin φ

ρcosφ

y

ρ

φ

и f (x, y)dxdy f (ρcosφ,ρsinφ) ρdρdφ .

D

D

Дифференциальный элемент площади

в полярных координатах

Геометрически выражение ρdρdφ является диф-

ференциалом площади в полярных координатах.

Действительно, если

разбить область интегрирова-

ния на элементарные ячейки Sij с помощью коор-

динатных линий: ρ ρ j

− окружности,

φ φi − лучи, то ρ j ρ j 1 ρ j , φi φi 1 φi .

Так как окружности ортогональны радиусам,

то площадь внутренних ячеек Sij

можно вычислить как разность площадей секторов с радиусами ρ j и ρ j 1 ρ j

и углом φi :
Sij	1	ρ j	j	2		1	ρ j	2						1	j	2
				φi					φi		ρ j	j					φi	ρ j j φi
	2					2								2

Ячейками неправильной формы пренебрегаем. Переходя к пределу, получим, что двумерный элемент площади в полярных координатах равен dS ρdρdφ.

Замечания

1.Интегрирование в полярной системе координат удобно использовать, когда область D ограничена координатными линиями полярной системы координат: лучами и дугами окружностей.

2.В полярных координатах внешний интеграл при сведе-

18