Ch_7_Integraly_po_figure

		В 0,1 .
		Вычислите криволинейный интеграл 1 рода
								dl										,	где L − отрезок прямой,																		3
																																		5
2	11.49			x	2		y					2	4																ln
		L
		соединяющий точки О 0, 0 и А 1, 2 .																											2
		Вычислите криволинейный интеграл 1 рода
				ydl						, где L − дуга линии
		L x 3z																											1
3	11.53	x t, y											t		2			, z				t	3			от О 0,0, 0 до
																													2
															2				3
													2
																			2
		А			2,				2,												.
															3
		Найдите массу всей астроиды
		x a cos3 t, y a sin3 t , если плотность																												9k a3
4	11.55	P							в каждой ее точке P выражается
																													64
		формулой P k																							xy			, где k 0 - коэф-
		фициент пропорциональности.
		Найдите массу всей лемнискаты
		2		a2 cos 2 , если плотность P в
5	11.57	каждой ее точке P выражается формулой																													k a2
		P k , где k 0 - коэффициент про-
		порциональности.
		Найдите массу дуги конической винтовой
		линии x aet																cost, y aet sin t, z aet ,
		если плотность в каждой ее точке P вы-																													ka
6	11.58																																				3
		ражается формулой ket , (где k 0 -																											2
		коэффициент пропорциональности), от точ-
		ки О 0,0, 0 до точки А a, 0, a .
		Найдите массу четверти окружности
7	11.60	x2 y2								r2 , расположенной в первом квад-																						r2
		ранте, если плотность в каждой ее точке
		пропорциональна абсциссе этой точки (ко-
		эффициент пропорциональности ).

69

Найдите массу полуокружности

x2 y2

r2 , расположенной верхней

8

11.61

полуплоскости, если плотность в каждой ее

4 r4

точке пропорциональна кубу ординаты

3

этой точки (коэффициент пропорциональ-

ности ).

Вычислите поверхностный интеграл 1 рода

x2 yzdσ , если S – часть плоскости

9

11.62

3

360

S

x y z 1 в первом октанте.

Вычислите поверхностный интеграл 1 рода

10

11.64

x2 y2 z2

dσ , если S – сфера

4

S

x2 y2 z2 1.

Определите момент инерции однородной

(плотности 1) боковой поверхности конуса

a4 2

11

11.67

z x2

y2 , 0 z a

2

относительно оси 0z .

70

IV. РАСЧЕТНАЯ РАБОТА

1. Титульный лист

Министерство образования и науки Российской Федерации Уральский федеральный университет

имени первого Президента России Б.Н. Ельцина Кафедра высшей математики

РАСЧЕТНАЯ РАБОТА

Интегралы по фигуре

Студент

Группа

Преподаватель

Вариант

Дата

Екатеринбург 2012

71

V. ФОРМУЛЫ

В этом разделе представлены основные формулы, условия применимости которых, были обсуждены выше. Поэтому свойства фигурирующих в них областей интегрирования и функций не оговариваются.

Двойной интеграл

Двойной интеграл в декартовых координатах

Область D ограничена линиями: y 1 (x),					y 2 (x) ,	x a ,
x b :
	f (x, y)dxdy	b 2 (x)
				f (x, y)dy dx .
D		a	1 ( x)

y

y 2 (x)

D

y 1(x)

0

a

b

x

Область D ограничена линиями x 1 ( y) ,					x 2 ( y),	y c,	y d :
	f (x, y)dxdy	d 2 ( y)
				f (x, y)dx dy .
D		c	1 ( y)

Замена переменных в двойном интеграле

Если x и y являются функциями переменных u и v : x x(u,v),

y y(u,v),

f (x, y)dxdy f (x(u,v), y(u,v)) | J | dudv ,

			D				D
где J		x		x			– якобиан преобразования.
		u		v
		y		y
		u		v

Двойной интеграл в полярных координатах

	f (x, y)dxdy f ( cos , sin ) d d					( J )
	D	D /
	Область D ограничена линиями: ,
	1 ( ) 2 ( ) :							D
			2 ( )
									2 ( )
	f ( , ) d d d			f ( , ) d .				1( )
							0
	D		1 ( )
	Область D ограничена линиями:			R1 R2 , 1 ( ) 2 ( ) :
		R1		2 ( )
	f ( , ) d d d				f ( , )d .
	D	R1		1 ( )

97

Приложения двойного интеграла

1	Площадь плоской фигуры					S dxdy		d d
						D		D /
	Объем цилиндрического тела,
	ограниченного сверху по-					V f (x, y)dxdy
2	верхностью z f (x, y) и по-
	строенного на основании D	в				D
	плоскости OXY ( f (x, y) 0)
	Масса неоднородной пла-					m (x, y)dxdy
3	стинки D с поверхностной
	плотностью (x, y)					D
	Статические моменты пла-		Sx y (x, y)dxdy , Sy						x (x, y)dxdy .
4	стинки D относительно ко-
	ординатных осей				D					D
	Координаты центра тяжести				x ( x, y )dxdy					y ( x, y )dxdy
5			x0		D		; y0			D	,
	пластинки D					m				m
	Моменты инерции пластинки		Ix y2 (x, y)dxdy ,					Iy	x2 (x, y)dxdy
6	D относительно координат-
	ных осей				D					D
	Момент инерции пластинки					I0 (x2 y2 ) (x, y)dxdy
7	D относительно начала ко-
	ординат					D

Тройной интеграл

Тройной интеграл в декартовых координатах

Область G ограничена снизу и сверху непрерыв-

ными поверхностями: z1 z1(x, y)			и z2	z2 (x, y) .
проекция G на плоскость OXY – область D :
f x ,	y , z d V dS	z 2 x , y	x,	y , z d z .
		f
G	D	z1 x , y
Область D ограничена линиями:
y y1 x ,	y y2 x , x a,b
			b	y2 x	z2 x,y

z				z2 (x, y)
			M 2
V					z1 (x, y)
			M1
0			c y		d
					y
a
x			M		D
b x

f x, y, z dxdydz dx			dy			f x, y, z dz .
G	a	y1 x			z1 x, y
Область D задана неравенствами c y d ,					x1(y) x x2 ( y):
	d x2 ( x)			z2 (x, y)
f (x, y, z)dxdydz dy			dx			f (x, y, z)dz .
V	c	x1 ( x)		z1( x, y)

98

Замена переменных в тройном интеграле

Если x x(u,v,t), y y(u,v,t), z z(u,v,t) ,

				x		x			x
якобиан перехода				u		v			t		, то
	J			y		y			y
				u		v			t
				z		z			z
				u		v			t

	f x, y, z dV		f u,v,t	J	dudvdt .
G		G			dV

Тройной интеграл в цилиндрических координатах

x cos ,	0	,
	0	2 ,
y sin ,
	z .
z z,

z

M ( , , z )

Якобиан перехода: J ρ, , z ρ ;

0

y

f (x, y, z)dxdydz f ( cos , sin , z) d d dz

x

V

V

.

Тройной интеграл в сферических координатах

x sin cos ,

0,

z

B

y sin sin ,

0 ,

M( , , )

z cos .

0 2 ,

Якобиан перехода:

J , ,

2 sin .

0

y

f x, y, z dxdydz

f

, ,

2

sin d d d .

x

A

V

V

f , , 2

2

2 ( )

2 ( , )

2 f , , d .

sin d d d d

sin d

V

1

1 ( )

1 ( , )

Приложения тройного интеграла

1

Объем тела

V dxdydz d d dz 2 sin d d d

V

V

V

Масса неодно-

2

родного тела с

m ( x,y,z )dxdydz

плотностью

V

γ(x, y, z)

99

		x0	x ( x, y, z)dxdydz		, y0	y ( x, y, z)dxdydz		,
			V			V
	Координаты		( x, y , z )dxdydz			( x, y, z)dxdydz
3	центра тяжести		V			V
				z (x, y, z)dxdydz
	тела
			z0	V			.
				(x, y, z)dxdydz
				V
			Ix ( y2 z2 ) (x, y, z)dxdydz ,
			V
4	Моменты инер-		Iy (x2 z2 ) (x, y, z)dxdydz ,
	ции тела		V
			Iz (x2 y2 ) (x, y, z)dxdydz
			V

VI. БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Пискунов, Николай Семенович. Дифференциальное и интегральное исчисления: учеб. пособие для студентов втузов : в 2 т. Т. 2 / Н. С. Пискунов. - Изд. стер. - М.: Интеграл-Пресс, 2004.

2.Бермант, Анисим Федорович. Краткий курс математического анализа: учебник для вузов / А. Ф. Бермант, И. Г. Араманович. - Изд. 11-е, стер. -

СПб.: Лань, 2005.

3.Сборник задач по математике для втузов: В 4 ч. Ч. 2: Введение в анализ. Дифференциальное и интегральное исчисление функций одной переменной. Дифференциальное исчисление функций нескольких переменных. Кратные интегралы. Дифференциальные уравнения / А. В. Ефимов, А. Ф. Каракулин, С. М. Коган и др. / Под ред. А. В. Ефимова, А. С. Поспелова. - 4-е изд., перераб. и доп. - М.: Физматлит, 2003.

4.Кузнецов, Леонид Антонович. Сборник задач по высшей математике. Типовые расчеты: учеб. пособие / Л. А. Кузнецов. - Изд. 3-е, испр. - СПб. ; М. ; Краснодар: Лань, 2005.

100

ПРИЛОЖЕНИЕ

ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

НАЗВАНИЕ

ВИД

УРАВНЕНИЕ

	1. Эллипсоид	1.	x2		y2		c2	1
			a2		b2		z2

2. Гиперболоиды:

	2.1. Однополостный	2.1.	x2		y2		z2	1
			a2		b2		c2

	2.2.
2.2. Двуполостный		x2		y2		z2	1
		a2		b2		c2

101

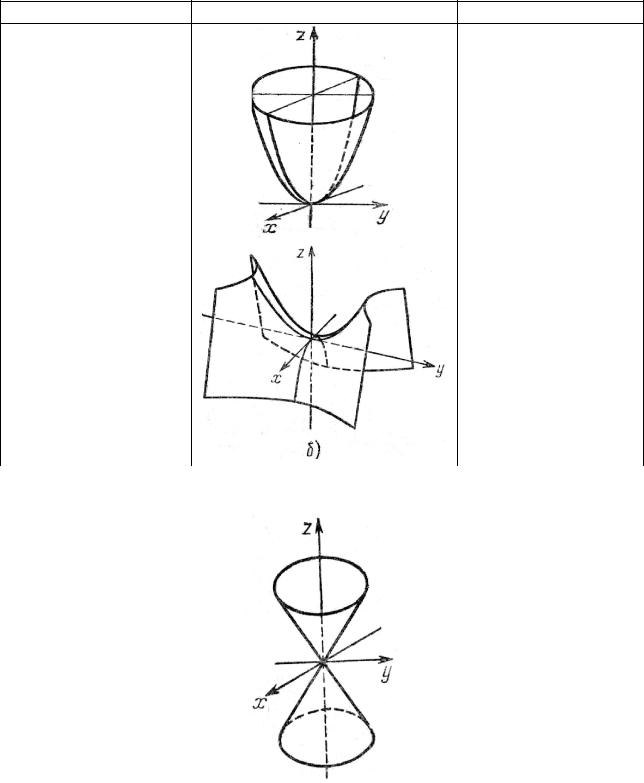
3. Параболоиды:

3.1. Эллиптический

3.1.

x2

y2

pz

a2

b2

3.2. Гиперболический

x2

y2

pz

3.2.

b2

a2

4. Конус

4.

x2

y2

z2

0

a2

b2

c2

102

5. Цилиндры:

	5.1. Эллиптический	5.1.	x2				y2	1
			a	2			b2
	5.2. Гиперболический	5.2.	x2				y2	1
			a	2			b2
	5.3 Параболический	y2			2 px,
		5.3.
		p 0

103