Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Высшая математика Часть 2

.pdf

Скачиваний:

458

Добавлен:

23.02.2015

Размер:

4.52 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 183 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

n1 = (3,2,4), n2		= (2,1,−3),
a = [n1 ×n2 ]=	i	j	k
	i	j	k
	3	2	4	= −10i +17 j − k ,
	2	1	−3

a ={−10,17,−1}.

Запишем канонические уравнения прямой: x−−101 = y17− 2 = z−−11 .

x =1−10t,

Параметрические уравнения прямой имеют вид: y = 2 +17t,

z =1− t.

17x +10 y −37 = 0,

Уравнения прямой в проекциях: x −10z +9 = 0,

y +17z −19 = 0.

Уравнения прямой, проходящей через две данные точки

Пусть даны две точки M1 (x1, y1, z1 )

и M2 (x2 , y2 , z2 ) . В качестве направ-

ляющего вектора прямой выберем вектор

M1M2 ={x2 − x1, y2 − y1, z2 − z1}, и

уравнения прямой, проходящей через две данные точки, примут вид:

x − x1

y − y1

z −z1

− x

− y

− z

ПРИМЕР: Составьте уравнения прямой,

проходящей через

две точки

M1 (1, −2,1) и M2 (3,1, −1) .

x −1

y + 2

z −1

→

x −1

y + 2

z −1

−1 −1

3 −1 1 + 2

− 2

Угол между двумя прямыми

Если a1 ={l1, m1, n1}

={l2 , m2 , n2}

направляющие

векторы прямых L1 и L2 ,

то абсолютная величина косинуса

угла между этими векторами

cosϕ =

l l + m m + n n

1 2

l2 + m2

+ n2

l2 + m2 + n2

дает угол между прямыми ϕ ≤

Условие параллельности и перпендикулярности двух прямых

Прямые будут параллельны, если их направляющие векторы a1 и a2

параллельны, то есть	l1	=	m1	=	n1
						.
	l2		m2		n2

Прямые будут перпендикулярны, если их направляющие векторы перпендикулярны, то есть l1l2 + m1m2 + n1n2 = 0 .

ПРИМЕР: Определите угол между двумя прямыми:

3x − 4 y − 2z = 0,		4x + y −6z − 2 = 0,
	2x + y − 2z = 0,		y −3z + 2 = 0.

Находим направляющие векторы данных прямых. Нормальные векторы плоскостей, задающих первую прямую, n1 ={3,−4,−2}, n2 ={2,1,−2}, и вторую пря-

мую, n3 ={4,1,−6}, n4 ={0,1,−3}.

Направляющие векторы первой и второй прямых:

a1 = [n1 ×n2 ]=

− 4

− 2

=10i + 2 j +11k ,

− 2

a2 =[n3 ×n4 ]=

4 1

−6

= 3i +12 j + 4k ,

0 1

−3

cosϕ =

10 3 + 2 12 +11 4

;

+ 22 +112 32 +122 + 42

102

195

ϕ= arccos19598 .

2.4.Прямая и плоскость Точка пересечения прямой и плоскости

Пусть известны уравнения прямой и плоскости:

L :	x − x0	=	y − y0	=	z − z0	; P : Ax + By +Cz + D = 0 .
	l		m		n

Координаты точки пересечения прямой и плоскости должны одновременно удовлетворять этим уравнениям.

1). Выражая две переменные через третью из уравнений прямой и подставляя их в уравнение плоскости, получим уравнение для одной переменной и найдем точку пересечения прямой и плоскости.

2). Можно перейти к параметрическим уравнениям прямой: x = x0 + lt, y = y0 + mt, z = z0 + nt ,

тогда подстановка переменных в уравнение плоскости P позволяет найти зна-

чение параметра	t0	= −	Ax0 + By0 +Cz0 + D	для координат точки пересечения пря-
			Al + Bm +Cn

мой и плоскости.

3). Если прямая задана общими уравнениями, точка пересечения может быть найдена как решение системы из трех уравнений плоскостей.

Уравнение пучка плоскостей, проходящих через прямую

Пусть прямая задана линией пересечения двух плоскостей:

A1 x + B1 y + C1 z + D1 = 0,A2 x + B2 y + C2 z + D2 = 0.

Возьмем любые отличные от нуля числа α и β и составим равенство

α ( A1 x + B1 y + C 1 z + D1 ) + β ( A2 x + B 2 y + C 2 z + D 2 ) = 0 .

Это равенство определяет произвольную плоскость, проходящую через ту же прямую, так как каждая тройка чисел (x, y, z) удовлетворяет этим двум равенствам. Совокупность всех плоскостей, проходящих через одну и ту же прямую,

называется пучком плоскостей. Если положить α ≠ 0 и λ = αβ , то уравнение

A1 x + B1 y +C1 z + D1 + λ( A2 x + B2 y +C2 z + D2 ) = 0

определяет все плоскости пучка, кроме второй из плоскостей, задающих прямую.

Угол между прямой и плоскостью

Угол ϕ между прямой и плоскостью определяется как угол между прямой и ее проекцией на плоскость. Пусть ψ – угол между вектором нормали n к

плоскости и направляющим вектором a				прямой. Если угол ψ острый, то
ϕ =	π	−ψ , если угол ψ тупой, то ϕ =ψ −	π	, т. е. ϕ =	π	−ψ	.

	2		2		2

sinϕ = sin

−ψ

cosψ

a )

Условия параллельности и перпендикулярности

прямой L :	x − x0	=	y − y0	=	z − z0	и плоскости P : Ax + By +Cz + D = 0
	l		m		n

Прямая L перпендикулярна плоскости P, если направляющий вектор прямой коллинеарен нормальному вектору плоскости, то есть

Al = mB = Cn .

Прямая L параллельна плоскости P, если направляющий вектор прямой перпендикулярен нормальному вектору плоскости, (a n) = 0, то есть

Al + Bm +Cn = 0.

3.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

3.1.Простейшие задачи на плоскости

Расстояние между двумя точками

Даны две точки M1(x1,y1) и M2(x2,y2). Расстояние между

ними равно длине вектора

M1M2 ={x2 − x1 ,y2 − y1} и

может быть вычислено по формуле

d =

M M

= (x − x )2

+(y − y )2

Деление отрезка в данном отношении

Точка M(x,y) делит отрезок M1M2 в отношении λ,

x − x1

y − y1

если

x − x

= y

− y

= λ .

М находятся по

формулам:

Координаты

точки

x +λ x

x =

;

1+λ

+λ y2

y =

1+λ

Координаты середины отрезка С получаются при М1М = ММ2, λ =1:

xc = x1 +2 x2 ,yc = y1 +2 y2 .

Площадь треугольника

Пусть треугольник задан координатами своих вершин:

М1(x1,y1), M2(x2,y2), M3(x3,y3).

x2 − x1

y2 − y1

S =

x3 − x1

y3 − y1

3.2. Прямая линия на плоскости

Прямая линия – одно из основных понятий геометрии. Если основой построения геометрии служит понятие расстояния между точками, то прямую можно определить как линию, вдоль которой расстояние между двумя точками является кратчайшим.

Уравнения прямой
Общее уравнение прямой на плоскости XOY получается из				общего
уравнения плоскости в пространстве при z= 0:

	Ax+By+C = 0.

Если А= 0 (В= 0), то прямая параллельна оси OX (оси OY).
Если С= 0, то прямая проходит через начало координат.
Если прямая проходит через точку (x0,y0) перпендикулярно				вектору
n = {A, B}, ее уравнение принимает вид:			.
n = {A, B}, ее уравнение принимает вид:		A(x − x0 ) + B( y − y0 ) = 0	.

Каноническое уравнение прямой

Если прямая проходит через точку (x0,y0) параллельно направляющему вектору a ={l,m}, то получаем каноническое и параметрические уравнения

прямой на плоскости в виде:

	x − x	0	=	y − y	0	и	x = x0 + lt,
		0			0
	l			m
	l			m			y = y0	+ mt,
где t - параметр, t (−∞,∞) .
где t - параметр, t (−∞,∞) .

Уравнение прямой, проходящей через две точки

Пусть на плоскости заданы две точки M1(x1,y1), M2(x2,y2). Уравнение прямой, проходящей через эти точки, можно записать как условие коллинеарности векторов

M1M2 и MM1 , где M(x,y) – произвольная точка прямой. Искомое уравнение получаем в виде

x − x1		=	y − y1			.
x	− x	=	y	2	− y	.
2	1			2	1

Уравнение прямой, проходящей через данную точку в заданном направлении

Пусть прямая составляет угол α с осью ох. Угловым коэффициентом прямой k называется число k = tgα .

Прямая может быть задана точкой М1(x1,y1) и угловым коэффициентом k или двумя точками М1(x1,y1) и М2(x2,y2).

Уравнение прямой с угловым коэффициентом k

может быть получено из общего уравнения прямой

Ax+By+C=0, если B ≠ 0 :

y = k x +b , где k = − BА и b = −CB .

Прямая пересекает ось oy в точке P(0,b).

Из уравнения прямой, проходящей через две точки, имеем

y − y =	y2 − y1		(x − x ) ,	y2 − y1		= tgα = k ,

1	x2	− x1	1	x2	− x1

y − y1 = k(x − x1).

Уравнение прямой в отрезках

Общее уравнение прямой Ax+By+C=0 может быть преобразовано к виду уравнения прямой “в отрезках”: ax + by =1 .

Прямая в отрезках пересекает ось Оx в точке А(а,0) и ось Оy в точке

В(0,b).

Нормальное уравнение прямой

Пусть известно расстояние от прямой до начала координат OP = p и угол α между перпендикуляром

к прямой и осью OX. Из нормального уравнения плоскости в пространстве, полагая z= 0 и учитывая, что

cos π	−α = sin α,
2
получаем нормальное уравнение прямой на плоскости в виде
		xcos α + ysin α − p = 0	.
Нормальное уравнение прямой можно получить из общего уравнения
прямой Ax+By+C= 0, умножив его на нормирующий множитель µ = ±				1	.
				A2 + B2	.

Знак числа µ должен быть противоположен знаку числа С.

Косинусы углов, образуемых прямой с осями координат, называются

направляющими косинусами прямой.

Если угол между прямой и осью OX равен α и угол между прямой и осью

OY равен β, то cos2 α + cos2 β =1.

Расстояние от точки до прямой

Расстояние d от точки M0(x0,y0) до прямой, задаваемой нормальным уравнением, равно модулю отклонения точки от прямой δ , d = |δ |:

d = Ax + By +C . A2 + B2

По этой формуле δ положительно, если точка М0 и начало координат лежат по разные стороны от прямой, в противном случае δ отрицательно.

Координаты точки пересечения двух прямых

Если прямые заданы уравнениями A1x+B1y+C1=0 и A2x+B2y+C2=0, то координаты точки их пересечения (x0, y0) получаются как решение системы уравнений

A1x + B1 y +C1 = 0,A2 x + B2 y +C2 = 0

по формулам Крамера в виде x =

, y =

, при

≠ 0.

А2

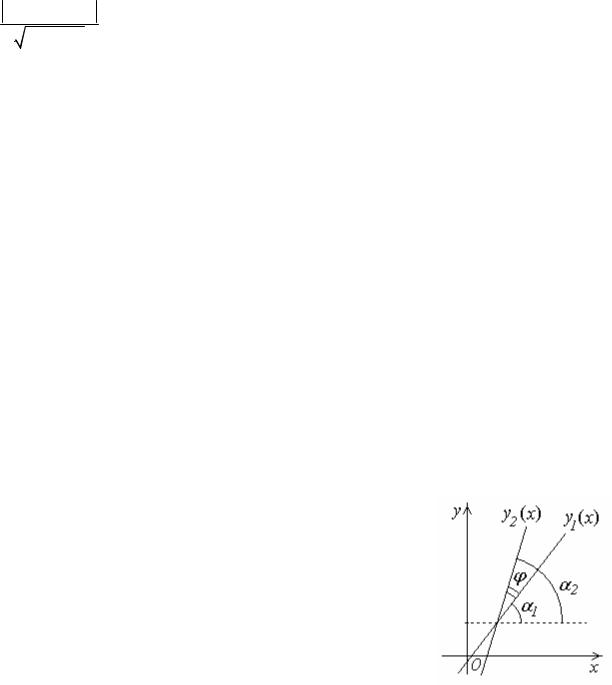
Угол между двумя прямыми

Пусть две прямые заданы уравнениями: y1 = k1x +b1,

y2 = k2 x +b2.

Острый угол ϕ пересечения этих прямых

(отсчитываемый против часовой стрелки) находится из следующих соотношений:

tgϕ = tg(α2	−α1 ) =		tgα2 − tgα1	=		k2 − k1
tgϕ = tg(α2	−α1 ) =	1	+ tgα1 tgα2	=	1	+ k2 k1
		1	+ tgα1 tgα2		1	+ k2 k1

Условие параллельности и перпендикулярности двух прямых

Если прямые заданы уравнениями A1x+B1y+C1=0 и A2x+B2y+C2=0, то они

параллельны, если A1 = B1 , и перпендикулярны, если A1 A2 + B1B2 = 0 .

A2 B2 Прямые y1=k1x+b1 и y2=k2x+b2:

параллельны друг другу, если ϕ = 0 , tgϕ = 0 : k1=k2;

перпендикулярны друг другу, если ϕ=	π , tgϕ → ∞:	k k		= −1	k = −	1	.
			2
	2	1			1	k2

3.3. Кривые второго порядка

Кривые второго порядка на плоскости определяются алгебраическими уравнениями второго порядка.

Эллипс

Эллипсом называется геометрическое место точек M(x,y), для которых сумма расстояний до двух заданных точек F1(+с,0) и F2(-с,0) (называемых фокусами эллипса) постоянна и равна 2а.

Вывод уравнения эллипса.

По определению F1M + F2M = 2a и F1F2 = 2c, значит, а>c. Воспользуемся формулой расстояния между двумя точками:

F M	= (x − c)2	+ y2	= r ,	F M	= (x + c)2	+ y2	= r .
1			1	2			2

По определению r1 + r2 = 2a . Подставим в это равенство r1 и r2: (x + c)2 + y2 + (x −c)2 + y2 = 2a .

Проделаем преобразования:

(x + c)2 + y2 = 2a − (x −c)2 + y2 ;

(x + c)2 + y2 = 4a2 − 4a (x −c)2 + y2 + (x −c)2 + y2 ; a (x −c)2 + y2 = a2 −cx;

(a2 −c2 )x2 + a2 y2 = a2 (a2 −c2 ). Если a2- c2=b2, то b2x2+a2y2=a2b2 и

x2	+	y2	=1	- каноническое уравнение эллипса.
a2		b2

Убедиться, что любая точка, координаты которой удовлетворяют этому уравнению, принадлежит эллипсу, можно следующим образом. Из каноничес-

кого уравнения получим, что y

= b

−

. Подставим это выражение в

соотношение

F1M

F2M

= 2a ,

взятое

виде

(x + c)2 + y2 +

(x −c)2 + y2 = 2a .

После

преобразований

получим

тождественное равенство.

Эллипс – центральная линия второго порядка, замкнутая линия, симметричная относительно осей и центра. Элементами эллипса являются: точка О - центр эллипса;

точки A, B, C, D - вершины эллипса;

точки F1(с,0), F2(-с,0) - фокусы эллипса;

2c - фокусное расстояние, которое вычисляется по формуле c = a2 −b2 ; АВ=2а и CD=2b - большая и малая оси эллипса; a и b - большая и малая полуоси эллипса;

e = ac , (e <1) - эксцентриситет эллипса, который вычисляется по формуле

e = 1− b2 . a2

Эксцентриситет определяется отношением осей эллипса и характеризует его форму: чем больше e, тем более вытянут эллипс вдоль большой оси. Прямые d1 и d2 , параллельные малой оси

эллипса и отстоящие от его центра на
расстояниях	d = ± a ,	называются
директрисами	e
директрисами	эллипса,	соответствующими
фокусам F1 и F2. Отношение расстояния любой
точки эллипса до фокуса к расстоянию ее до			r1		r2
соответствующей директрисы постоянно и равно эксцентриситету			r1	=	r2		= e .
			d	=			= e .
			d		d	2
			1			2

Окружность

Окружность представляет собой геометрическое место точек, равноудаленных от точки О, называемой центром окружности. Уравнение окружности можно

получить из уравнения эллипса при a=b=R: x2+y2=R2.

Гипербола

Гиперболой называется геометрическое место точек M(x,y), для которых абсолютная величина разности расстояний до двух заданных точек F1(+c,0) и F2(-c,0) (называемых фокусами гиперболы) постоянна и равна 2а.

Вывод уравнения гиперболы.

По определению F1M − F2 M = 2a и F1 F2 = 2c, значит, а<с.