Оглавление

Оглавление 1

Глава II. Аппроксимация и интерполяция 2

§ 1. Основные понятия 2

§ 2. Существование и единственность интерполяционного многочлена 3

§ 3. Интерполяционный многочлен Лагранжа 5

§ 4. Погрешность интерполяционного многочлена Лагранжа 6

§ 5. Минимизация погрешности интерполяционного многочлена Лагранжа. Многочлен Чебышева 7

§ 6. Схема Эйткена 9

§ 7. Численное дифференцирование 10

§ 8. Погрешность простейших формул численного дифференцирования 13

§ 9. Разделенные разности. Многочлен Ньютона. 15

§ 10. Интерполяция с кратными узлами 17

§ 11. Кубическая сплайн-интерполяция 19

Глава III. Численное интегрирование 22

§ 1. Простейшие квадратурные формулы. Составные формулы 22

§ 2. Метод неопределенных коэффициентов 23

§ 3. Формулы Ньютона-Котеса 25

§ 4. Формулы Гаусса 27

§ 5. Погрешность квадратурных формул. Правило Рунге. 30

Глава IV. Численные методы алгебры 32

§1. Системы линейных уравнений: метод простых итераций, метод Зейделя 32

§2. Метод наискорейшего спуска 35

§ 3. Обратная интерполяция для решения нелинейных уравнений 36

§ 5. Системы нелинейных уравнений: метод Ньютона 41

§ 6. Методы спуска 44

§ 2. Метод Эйлера. Методы Рунге-Кутта 48

§ 3. Конечно-разностные методы 50

§ 4. Уравнения второго порядка 51

ГлаваII. Аппроксимация и интерполяция

§ 1. Основные понятия

Задача:

Дано: x₀, x₁, ..., x_n — узлы,

f(x₀), f(x₁), ..., f(x_n) — значения f(x) в узлах.

Найти: функцию g(x), такую, что

g(x_i) = f(x_i), i=0,...,n.

Если в дальнейшем нужно вычислить значение g(x) для , то говорят об интерполяции функции.

Если (т.е. лежит за пределами отрезка, содержащего узлы), то говорят об экстраполяции.

Примером решения задачи является использование многочлена Тейлора m-ой степени:

.

Для x₀=0 можно использовать известные разложения для функций:

.

Погрешность метода — остаточный член формулы Тейлора в форме Лагранжа:

, где c лежит между x и x₀.

Кроме того, если не принадлежит интервалу сходимости ряда Тейлора, то погрешность не уменьшается.

§ 2. Существование и единственность интерполяционного многочлена

Задача:

Дано: x₀, x₁, ..., x_n — узлы,

f₀, f₁, ..., f_n — значения f(x) в узлах.

Найти: , такой, что

L_m(x_i) = f_i, i=0,...,n.

Теорема.

Существует единственный многочлен степени , удовлетворяющий условиям задачи.

Док-во:

Чтобы найти многочлен L_m(x) нужно найти коэффициенты a₀,a₁,...a_n.

Они должны удовлетворять СЛУ

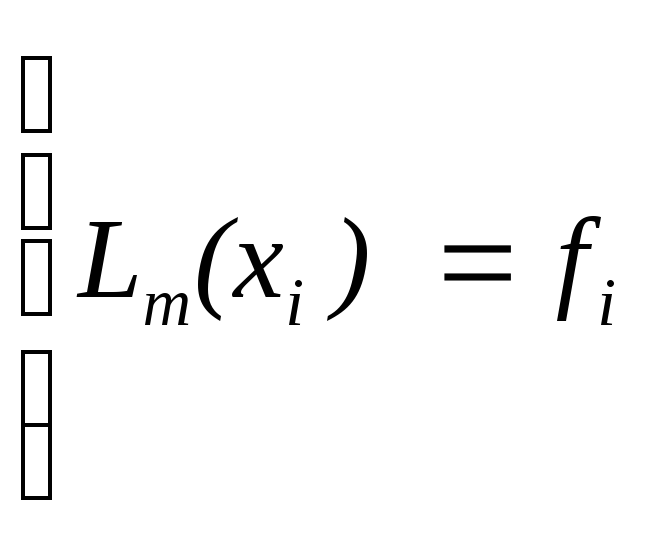, i=0,...,n.

В системе (m+1) неизвестных, (n+1) уравнение.

Если система крамеровская, то решение существует и единственное.

Пусть m+1= n+1, т.е. m=n.

Главный определитель системы

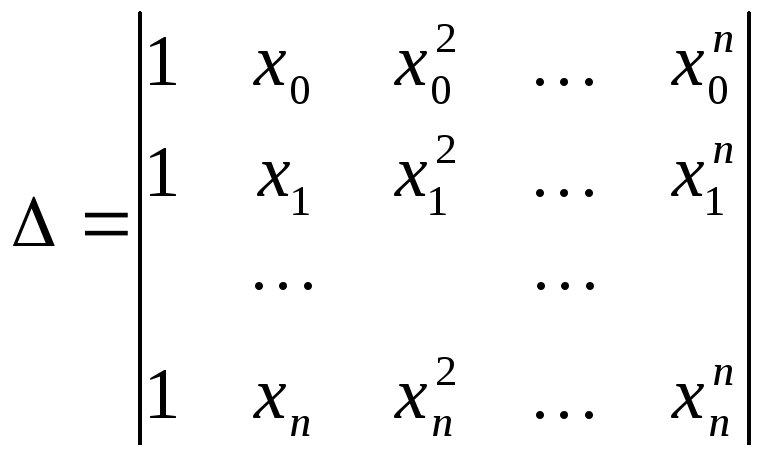—определитель Вандермонда.

. Если все узлы различны, то . Теорема доказана.

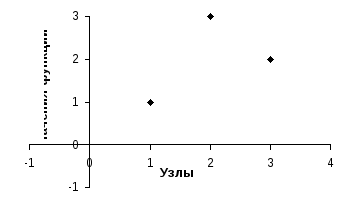
Замечание (иллюстрация):

Если m<n, СЛУ может быть несовместна.

Например, m=1, n=2, найти линейную функцию (прямую), проходящую через три точки:

Е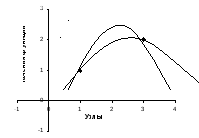слиm>n, СЛУ имеет бесконечно много решений.

Например, m=2, n=1, найти квадратичную функцию (параболу), проходящую через две точки: