матан

V ={(x, y) D, x

4

y

2

≤ z ≤π},

D ={−1≤x ≤+1,

1 (

)

≤ y ≤1},

2

x +1

π

sin x4 y2 dz

dxdy =

∫∫sin x4 y2

sin z

dxdy =−∫∫1 dxdy =−1.

→=∫∫ ∫

cos z

1

π

D x4 y2

D

x4 y2

D

Здесь воспользовались геометрическим смыслом двойного интеграла от функции, равной 1 . В данном случае это площадь прямоугольного треугольника с катетами длиной

1 и 2.

№ 34.3.	неоднородного тела V с объемной плотностью
При нахождении центра масс
ρ =ρ(r ) =ρ(x, y, z) и массой
m =∫∫∫ρ(r )dV =∫∫∫ρ(x, y, z)dxdydz
V	V

воспользуемся определением центра масс системы материальных точек. Разобьем объем

V поверхностями

на малые,

попарно не

налегающие

части

Vk с

массами

∆k m ≈ ρ(ξk )∆kV = ρ(ξk ,ηk ,ζk )∆kV ,

настолько

малые,

что

каждую

можно

рассматривать как материальную точку ξk =(ξk ,ηk ,ζk ) . Тогда

= m ∫∫∫xρ(x, y, z)dxdydz

x0

1

V

1

n

n

∫∫∫r ρ(r )dV

∫∫∫yρ(x, y, z)dxdydz

r0 ≈

∑ξk ∆k m ≈

1

∑ξk ρ(ξk )∆kV d→→0

1

y0

=

1

m

m

m

m

k =1

k =1

V

V

1

∫∫∫zρ(x, y, z)dxdydz

z0 =

m

V

Плоскости, ограничивающие объем V ,

необходимо построить достаточно точно.

V ={(x, y) D, 0≤z ≤3− 1 (6x +3y)},

2

D ={0 ≤ x ≤1,

0 ≤ y ≤2(1− x)}

Найдем массу тела:

3−

1

(6 x+3 y)

)dxdy=ρ∫∫(3−12 (6x+3y))dxdy=

m=∫∫∫ρ(x, y, z)dxdydz=ρ∫∫∫1 dxdydz=ρ∫∫(

2

∫

1 dz

V

V

D

0

D

1

2(1−x)

1

=ρ∫(

∫ (3− 12 (6x +3y))dy )dx =ρ∫(3(1− x) y − 43 y2 )

2(1−x)

dx =

0

0

0

0

=ρ∫1 (3(1− x)2(1− x)− 43 4(1− x)2 )dx =3ρ∫1 (1−x)2 dx =ρ.

0

0

Найдем координаты центра масс:

3−1 (6 x+3 y)

1

ρ

ρ

2

x0 =

m

∫∫∫xρ(x, y, z)dxdydz=

m

∫∫∫x dxdydz=

m

∫∫(

∫

x dz

)dxdy=

V

V

D

0

=

ρ

∫∫x(3−12 (6x+3y))dxdy=

ρ

∫1 (

x2(1∫−x) (3(1−x)−23 y)dy )dx=

m

m

D

0

0

1

)

1

)dx=3

1

ρ

3

2

2(1−x)

ρ

∫x(3(1−x)2(1−x)−

3

2

ρ

2

3 ρ

3

=

∫x(3(1−x) y−

4 y

0

dx=

4 4(1−x)

∫x(1−x)

dx= 4

=

4 .

m

m

m

m

0

0

1(6 x+3 y)

0

3−

1

ρ

ρ

2

∫

y0 =m

y dz

∫∫∫yρ(x, y, z)dxdydz=m ∫∫∫y dxdydz=m ∫∫

dxdy=

V

V

D

0

=

ρ

∫∫y (3−12 (6x+3y))dxdy=

ρ

∫1 (

2(1∫−x) (3(1−x) y−23 y2 )dy

)dx=

m

m

D

0

0

1

)

1

)dx=

1

ρ

∫(3

(1−x)

1

2

1

3

2(1−x)

ρ

∫(3(1−x)

1

2

1

3

2ρ

∫(1−x)

3

2ρ

1

=

2 y

−2 y

dx=

2

4(1−x)

−2

8(1−x)

m

dx=

=

2 .

m

0

m

4m

0

0

0

3−1(6x+3 y)

1

ρ

ρ

2

z0 =m

∫∫∫zρ(x, y, z)dxdydz=m ∫∫∫z dxdydz=m

∫∫

∫

z dz

dxdy=

V

V

D

0

=

ρ

∫∫(3−12 (6x+3y))2 dxdy=29mρ ∫1 (

2(1∫−x) ((1−x)−12 y)2

dy

)dx=

2m

D

0

0

1

2(1−x)

1

=29mρ ∫(

∫ ((1−x)2 −(1−x) y+14 y2 )dy )dx=29mρ ∫((1−x)2

y−(1−x)12 y2 +

1

y3 )

2(1−x)

dx=

12

0

0

0

0

1

)

1

9ρ

∫(

(1−x)

2

y−(1−x)

1

2

1

3

2(1−x)

3ρ

∫(1−x)

3

3ρ

3

=2m

2 y

+

y

0

dx=

dx =8m=8 .

12

2m

0

0

№ 34.4.

V =∫∫∫1 dxdydz =→

V

Выделим среди поверхностей { z = xy, z =0, x + y =1}, ограничивающих объем V , те, уравнения которых не содержат переменной z . В данном примере прямая {y =1 − x} не

ограничивает никакую область	D , так что поверхности { z = xy, z = 0} необходимо
построить достаточно точно:	z = xy – седловая поверхность, z = 0 – горизонтальная
плоскость.

Из рисунка видно, что играет роль области									D ,	“нижней” и “верхней” поверхностей
{z = 0 ≤ z = xy,						(x, y) D} .
Итак,					V ={(x, y) D, 0 ≤ z ≤ xy}, D ={0 ≤ x ≤1, 0 ≤ y ≤1− x}
→=∫∫		xy			dxdy =∫∫xy dxdy		1	1−x	)	1	1−x
		∫1 dz					=∫(	∫ xy dy		dx =∫(	x ∫ y dy )dx =
D		0				D	0	0		0	0
1						1	1
=∫x 12 y2				1−x	dx = 12 ∫x (1− x)2 dx = 12 ∫(x −2x2 + x3 )dx = 12 (12 x2 − 32 x3 + 14 x4 )								1	1
													0 =		.
				0										24
0						0	0

Сравнить нахождение объема “криволинейного цилиндра” с помощью тройного с нахождением с помощью двойного интеграла:

V =∫∫∫1 dxdydz =[V ={(x, y) D,	fH (x, y)≤z ≤ fB (x, y)}]=∫∫(	fB (∫x, y)	1 dz )dxdy =
V	D	fH ( x, y)

=∫∫( fB (x, y) − fH (x, y))dxdy

D

35. Тройные интегралы. Переход к цилиндрическим координатам

Условия.

№ 35.1. Найти массу тела, ограниченного заданными поверхностями, с объемной плотностью ρ = ρ(x, y, z) .

z = x2 + y2 , z =0, x2 + y2 =a2 ;	z = x2 + y2 , z =0, x2 + y2 =a2 ;
ρ =(x2 + y2 ) z2 ;	ρ =(x2 + y2 ) z;

№ 35.2. Найти заряд тела, ограниченного заданными поверхностями, с объемной плотностью ρ = ρ(x, y, z) .

z = x2 + y2 , z =0, x2 + y2 =ay;	z = x2 + y2 , z =0, x2 + y2 =ax;
ρ =(x2 + y2 ) z;	ρ = x2 + y2 z;

№ 35.3. Найти центр масс тела, ограниченного заданными поверхностями, с объемной плотностью ρ = ρ(x, y, z) .

z = x2 + y2 , z =a; ρ =(x2 + y2 )2 z	z = x2 + y2 , z =a; ρ =(x2 + y2 ) z3 ;

Найти объем тела, ограниченного поверхностями.

	№ 35.4	z = x2 + y2 ,				z =0,	x2 + y2 =ax.
	№ 35.5	x2 + y2 + z2 =2az,					z ≥ x2 + y2 ;
	№ 35.6	z =	x2	+	y2	, z =1.
			a2		b2

№ 35.4	z = x2 + y2 ,					z =0, x2 + y2 =ay.
№ 35.5	z =2 −x2 − y2 , z = x2 + y2
№ 35.6	z =	x2	+	y2	,	z =1.
		a2
				b2

Теория.

∫∫∫f (x2 + y2 , z)dxdydz =∫∫∫f (r2 , z) r dzdrdϕ

V Ω

Решения.

№ 35.1.

m =∫∫∫ρ (x, y, z)dxdydz =∫∫∫(x2 + y2 ) z2 dxdydz =→

V V

Выделим среди поверхностей {z = x2 + y2 , z =0, x2 + y2 =a2 }, ограничивающих объем V , те, уравнения которых не содержат переменной z . На плоскости xOy эти уравнения

задают некоторые кривые, а в пространстве – цилиндрические поверхности, параллельные оси Oz , в основании которых лежат эти кривые. В данном примере окружность

{x2 + y2 =a2 } ограничивает круг	D радиуса a с центром в начале координат (0,0) ,	так
что поверхности {z =0 ≤ z =	x2 + y2 , (x, y) D}, играющие роль “нижней”	и
“верхней”, достаточно построить схематично.

Учитывая

вид подынтегральной

функции

f (x2 + y2 , z)

и

“цилиндрическую” форму

объема V , перейдем к цилиндрическим координатам.

Поскольку

z = x2 + y2 → z = r2 =r,

x2 + y2 =a2 → r2 =a2 r =a,

то

V ={(x, y) D ={x2 + y2 ≤a2 }, 0≤ z ≤ x2 + y2 }→

→Ω={(r,ϕ) ∆={r ≤a},

0≤ z ≤r}={0≤ϕ ≤2π,

0≤r ≤a, 0≤ z ≤r}.

Имеем:

2π

a

r

a

r

→=∫∫∫r

2

2

(

3

2

dz )dr

(

3

2

)dr =

z

r drdϕdz =

∫

∫

∫r

z

dϕ =2π ∫

r

∫z

dz

Ω

0

0

0

0

0

a

3 z3

r

)dr =

2π

a

6

2π r7

a

2

7

=2π ∫(

r

0

3

∫r

dr =

3

0 =

πa

.

3

7

21

0

0

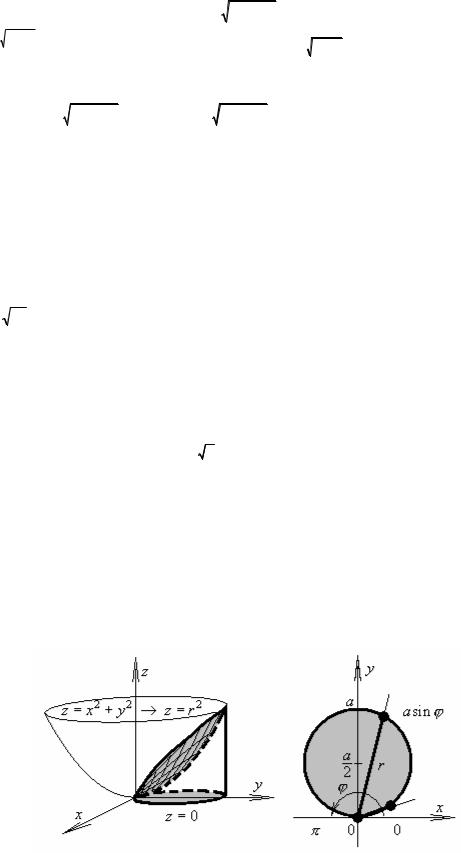
Сравнить.

m =∫∫∫ρ (x, y, z)dxdydz =∫∫∫(x2 + y2 )

z2 dxdydz =→

V

V

V ={(x, y) D, 0≤z ≤ x2 + y2 },

D ={x2 + y2 ≤a2 },

→=∫∫(

x2∫+ y2

(x2 + y2 ) z2 dz

)dxdy =∫∫(x2 + y2 )

13 z3

0x2 + y2

dxdy =

D

0

D

=13 ∫∫(x2 + y2 )(

x2 + y2 )3dxdy =13 ∫∫( x2 + y2 )5 dxdy =→

D

D

f (x2 + y2 )

Учитывая вид подынтегральной функции

и “круговую”

форму области D ,

перейдем к полярным координатам.

Поскольку

x2 + y2 =a2 →r =a ,

то

D ={x2 + y2 ≤a2 } → ∆={r ≤a}={0 ≤ϕ ≤2π, 0 ≤r ≤a}.

Тогда

2π

a

a

1

2 5

1

5

2π

6

2π r7

a

2

7

→=

3

∫∫

(

r )

rdrdϕ =

3

∫

∫

r

rdr

3

∫

r dr =

3

0

πa .

7

21

dϕ =

=

∆

0

0

0

Замечание. Цилиндрические координаты можно назвать еще “декартово-полярными”.

№ 35.2.

q =∫∫∫ρ (x, y, z)dxdydz =∫∫∫(x2 + y2 )

zdxdydz =→

V

V

Выделим среди поверхностей {z = x2 + y2 ,

z =0,

x2 + y2 =ay}, ограничивающих объем

V ,

те,

уравнения которых не содержат переменной z .

В данном примере окружность

{x

2

+ y

2

= ay} ограничивает круг

D ={ x

2

a

2

a

2

a

+(y − 2 )

≤(2 )

} радиуса 2 с центром в точке

(0, a2 ), так что поверхности {z =0

≤

z = x2 + y2 ,

(x, y) D} , играющие роль “нижней” и

“верхней”, достаточно построить схематично.

Учитывая вид подынтегральной функции f (x2 + y2 , z) и “цилиндрическую” форму

объема V , перейдем к цилиндрическим координатам. Поскольку

z = x2 + y2 → z =r2 , x2 + y2 =ay → r2 =ar sinϕ r =a sin ϕ,

то

V ={(x, y) D ={x2 + y2 ≤ay}, 0≤ z ≤ x2 + y2}→

→Ω={(r,ϕ) ∆={r ≤a sinϕ},

0≤ z ≤r2}={0≤ϕ ≤π,

0≤r ≤a sinϕ,

0≤ z ≤r2}.

Имеем:

π

a sinϕ

(

r

2

)dr

π

a sinϕ

3

r

2

∫∫∫

∫

∫

3

∫

∫

∫

0

→=

r2

z r drdϕdz =

r3

z dz

r3 2 z 2

dr

dϕ =

dϕ =

Ω

a sinϕ

0

0

0

0

0

2

π

r6 dr

2

π

r

7

a sinϕ

2

a7

π

sin7

2

a7

π

sin6 ϕd cosϕ =

=

dϕ =

dϕ =

ϕdϕ

=−

3 ∫

∫

3

∫ 7

0

21

∫

21

∫

0

0

0

0

0

=−

2

a7 ∫π (1−cos2 ϕ)3 d cosϕ =−

2

a7

−∫1(1−t2 )3 dt =

4

a7

+∫1(1−t2 )3 dt =

21

21

21

0

+1

0

+1

= 214 a7 ∫(1−3t2 +3t4 −t6 )dt = 214 a7 1635 .

0

№ 35.3.

Из физических понятий очевидно, что центр масс однородного тела с круговой симметрией находится на его оси: (x0 , y0 , z0 ) = (0,0,?). Цель приведенных ниже расчетов,

в частности, показать адекватность математических формул интуитивным представлениям.

Среди поверхностей {z = x2 + y2 , z =a}, ограничивающих объем V , нет таких, уравнения которых не содержат переменной z , так что обе поверхности необходимо построить достаточно точно: z = x2 + y2 – круговой конус, z = a – плоскость

Из рисунка видно, что играет роль области D , “нижней” и “верхней” поверхностей

V ={(x, y) D ={x2 + y2 ≤a2 }, x2 + y2 ≤ z ≤a}.

Найдем массу тела:

m =∫∫∫ρ(x, y, z)dxdydz =∫∫∫(x2 + y2 )2 z dxdydz =→

V

V

Учитывая вид

подынтегральной

функции

f (x2 + y2 , z)

и “цилиндрическую”

форму

объема V , перейдем к цилиндрическим координатам.

Поскольку

z = x2 + y2 → z = r2 =r,

x2 + y2 =a2 → r2 =a2 r =a,

то

V → Ω = {(r,ϕ) ∆ = {r ≤ a}, r ≤ z ≤ a} = {0 ≤ ϕ ≤ 2π, 0 ≤ r ≤ a, r ≤ z ≤ a}.

Имеем

2π

a

a

a

a

a

a

→=∫∫∫r4 z r drdϕdz= ∫(

∫(

∫r5 z dz )dr

)dϕ=2π ∫r5 (

∫zdz

)dr =2π∫r5 (

z2

)dr =

r

2

Ω

0

0

r

0

r

0

a

r6

r8

a

1

=π ∫(a2r5 −r7 )dr =π (a2

−

)

0 =

πa8.

6

8

24

0

Далее найдем

координаты центра масс, учитывая симметрию тела относительно

координатных

плоскостей

xOz,

yOz

и

нечетность

подынтегральных

функций

относительно переменных x,

y :

x0 =

1

∫∫∫xρ (x, y, z)dxdydz =

1

∫∫∫x (x2 + y2 )2 z dxdydz =0,

m

m

V

V

y0 = m1 ∫∫∫yρ (x,

V

z0 = m1 ∫∫∫zρ (x,

		V
		2π		a	a
=	1	∫		∫(	∫
	m
0				0	r

y, z)dxdydz = m1 ∫∫∫y (x2 + y2 )2 z dxdydz =0.

V

y, z)dxdydz =

1

∫∫∫z (x2 + y2 )2 z dxdydz =

1

∫∫∫z r4

z r drdϕdz =

m

m

V

Ω

r5 z2 dz )dr

a

r5 (

a

a

r5 (

3

a

)dr =

∫

∫

∫

m

m

3

r

dϕ =2π

1

z2 dz )dr =2π 1

z

0

r

0

	2	a							2	π (a	3 r6			r9	)		a	1				8
		π ∫(a	3		5		8	)dr =												9
=				r		−r							−				0 =		πa		=	9 a.
	3m								3m			6		9				27m
		0

№ 35.4.

Выделим среди поверхностей {z = x2 + y2 ,

z =0,

x2 + y2 =ax}, ограничивающих объем

V , те, уравнения которых не содержат переменной

z .

В данном примере окружность

{x

2

+ y

2

=ax} ограничивает круг

D ={ (x −

a

2

2

≤(

a

2

a

2 )

+ y

2 )

} радиуса 2 с центром в точке

(a2 ,0), так что поверхности {z =0

≤ z = x2 + y2 ,

(x, y) D} , играющие роль “нижней” и

“верхней”, достаточно построить схематично.

V =∫∫∫1 dxdydz =→

V

Учитывая “цилиндрическую” форму объема V , перейдем к цилиндрическим координатам.

Поскольку

			z = x2 + y2 → z =r2 ,						x2 + y2 =ax → r2 =ar cosϕ								r =a cosϕ,
то
V ={(x, y) D ={x2 + y2 ≤ax}, 0≤z ≤x2 + y2 }→
			→Ω={(r,ϕ) ∆={r ≤a cosϕ},								0≤ z ≤r2 }={−π				≤ϕ ≤+π , 0≤r ≤a cosϕ, 0≤ z ≤r2 }.
													2			2
Имеем:			+π									+π						+π
					a cosϕ		r	2					a cosϕ
			2									2							2	4			a cosϕ
→=∫∫∫ r drdϕdz = ∫					∫	(	∫		r dz		)dr dϕ = ∫				∫	r r2 dr	dϕ = ∫			r			0	dϕ =
																				4
Ω			−π		0		0					−π			0			−π
			2									2							2
		+π			+π										+π
= a	4	2	cos4 ϕdϕ = a	4	2	+2 cos 2ϕ +				1+cos 4ϕ				4	2	3 dϕ +0	+	0 = 3a	4	π.
		∫			1						2	dϕ = a
4			16		∫								16 ∫			2		32
		−π			−π										−π
		2			2										2

№ 35.5.

x2 + y2 + z2 =2az, z ≥ x2 + y2 ;

Среди	поверхностей {x2 + y2 + z2 =2az, z = x2 + y2 }, ограничивающих объем V , нет
таких,	уравнения которых не содержат переменной	z ,	так что	обе поверхности
необходимо построить достаточно точно:
	x2 + y2 + z2 =2az x2 + y2 +(z −a)2 =a2
- “смещенная” сфера радиуса a с центром в точке (0,0, a) ,		z =	x2 + y2	– круговой конус.

Из рисунка видно, что играет роль области D , “нижней” и “верхней” поверхностей

V ={(x, y) D ={x2 + y2 ≤a2 }, x2 + y2 ≤ z ≤a + a2 −(x2 + y2 )}.

V = ∫∫∫1 dxdydz =→

V

Учитывая “цилиндрическую” форму объема V , перейдем к цилиндрическим координатам.

Поскольку

z = x2 + y2 → z = r2 =r,

z =a + a2 −(x2 + y2 ) → z =a + a2 −r2 ,

то

V →Ω={(r,ϕ) ∆={r ≤a},

r ≤ z ≤a +

a2 −r2 }={0≤ϕ ≤2π,

0 ≤r ≤a,

r ≤ z ≤a + a2 −r2 }.

Имеем:

2π

a

a+ a2

−r2

r dz

)dr

a

a

−r

−r )dr =

→=∫∫∫r drdϕdz = ∫

∫(

∫

dϕ =2π ∫r (a +

2

2

Ω

0

0

r

0

=2π

a

(ar −r2 +r a2

−r2

)dr =

2π

1 r2 −1 r3 − 1 (a2

−r2 )

3

a

=πa3 .

∫

a

2

2

3

3

0

0