матан

С.Н. Зиненко

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Функции нескольких переменных

(теория, задачи, решения)

УЧЕБНОЕ ПОСОБИЕ

2004

УДК 517

ББК 22.1

Зиненко С.Н. МАТЕМАТИЧЕСКИЙ АНАЛИЗ: в 2-х частях. - Ч.2. Функции нескольких переменных. Учебное пособие. – Харьков: ХНУ, 2004. – 132 с.

В учебном пособии приводится материал по математическому анализу, изучаемый на практических занятиях во II семестре студентами I курса физического факультета. В соответствии с программой курса, материал разбит на 25 занятий, затрагивающих следующие темы: дифференцирование и интегрирование функций нескольких переменных, ряды и интегралы с параметром. В начале каждого занятия приводится минимально необходимый для решения и понимания задач теоретический материал. Практически все задачи сопровождаются подробным решением. Комментарии к решению задач настолько подробны, что изучение соответствующего материала возможно проводить самостоятельно, даже студентам, со слабой математической подготовкой. Задачи, предлагаемые для самостоятельной работы, полностью аналогичны аудиторным заданиям.

Для студентов физического и радиофизического факультетов.

Рецензенты:

Ю.В. Гандель– докторфизико-математическихнаук, профессоркафедрыматематической физикиивычислительнойматематикиХарьковскогонациональногоуниверситета им. В.Н. Каразина.

Утверждено к печати ученым советом физического факультета Харьковского национального университета им. В.Н. Каразина.

© Харьковский национальный университет им. В.Н Каразина, 2004

© Зиненко С.Н., 2004

Содержание

Дифференцирование функций

26.Частные производные и дифференциал функции. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

27.Производная по направлению. Градиент. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

28. Дифференцирование сложной функции. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 29. Производные и дифференциалы высшего порядка. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 30. Экстремум функции. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 31. Элементы дифференциальной геометрии. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

Интегрирование функций

32. Двойные интегралы. Физические и геометрические приложения. . . . . . . . . . . . . . . . . . 35 33. Двойные интегралы. Переход к полярным координатам. . . . . . . . . . . . . . . . . . . . . . . . . 41 34. Тройные интегралы. Физические и геометрические приложения. . . . . . . . . . . . . . . . . . 48 35. Тройные интегралы. Переход к цилиндрическим координатам. . . . . . . . . . . . . . . . . . . 54 36. Тройные интегралы. Переход к сферическим координатам. . . . . . . . . . . . . . . . . . . . . . . 62

37.Криволинейные интегралы по длине (масса, заряд). . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67

38.Криволинейные интегралы по координатам (работа силы). . . . . . . . . . . . . . . . . . . . . . . 70

39. Поверхностные интегралы по площади (масса, заряд). . . . . . . . . . . . . . . . . . . . . . . . . . . 74 40. Поверхностные интегралы по координатам (поток вектора). . . . . . . . . . . . . . . . . . . . . . 80

Ряды и интегралы с параметром

41. Сходимость несобственных интегралов. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85 42. Числовые ряды. Признаки сравнения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91

43.Числовые ряды. Признаки Даламбера, Коши, Лейбница. . . . . . . . . . . . . . . . . . . . . . . . . 95

44.Степенные ряды. Ряды Тейлора. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . 100

45. Ряды Фурье. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . 106 46. Ряды Фурье по Cos и по Sin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112 47. Интегралы Фурье. Cos - и Sin - преобразования Фурье. . . . . . . . . . . . . . . . . . . . . . . . . 117 48. Интегралы с параметром.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121 49. Интеграл Эйлера-Пуассона.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126 50. Эйлеровы интегралы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129

26. Частные производные и дифференциал функции

Условия.

Найти частные производные

fx′,...

и дифференциал df

функции f (x,...) .

№ 26.1.

z =

x

№ 26.1.

z = xy

№ 26.2.

z =x2 4 y3 −5 x y3

y

№ 26.2.

z =x3 y +3 x y5

3

№ 26.3.

z =arctg (x2 3 y )

№ 26.3.

z =arcsin

x

y

y

№ 26.4.

z =ln tg

x3

№ 26.4.

z =ctg arcsin

y

x2

z =(sin x)cos y

№ 26.5.

z =xy

№ 26.5.

№ 26.6.

u =x

y

№ 26.6.

u =zxy2

z

№ 26.7.

u =

sin (xy2 )

№ 26.7.

u =

tg (x2 y)

cos z

arctg z

№ 26.8.

u = xyz

№ 26.8.

u = z yx

№ 26.9. Заменяя приращение функции

дифференциалом, найти приближенно

следующие значения.

1,11,8

3 1,1 4 0,8

№ 26.10. Насколько приближенно изменились

периметр и площадь

параллелограмма, у которого

стороны

треугольника,

у которого стороны x,

y и

x, y

и угол между ними α

изменились

угол между

ними

α изменились

на

на ∆x,

∆y, ∆α .

∆x, ∆y, ∆α .

№ 26.11. Насколько приближенно изменились

площади основания, боковой

поверхности и объем

кругового конуса, у которого радиус

правильной треугольной пирамиды, у

основания r

и высота h изменились на

которой длина стороны основания a и

∆r,

∆h .

высота h изменились на ∆a, ∆h .

Теория.

Частная производная функции u = f (x, y, z,...) нескольких переменных по переменной x - это обычная производная, если на остальные переменные y, z,... временно смотреть как

на фиксированные параметры (т.е. функцию воспринимать, как функцию одной переменной x )

u′	= ∂f (x, y, z,...)	= lim	f (x +∆x, y, z,...) − f (x, y, z,...)	.
x	∂x	∆x→0	∆x

Функция u = f (x, y, z,...) называется дифференцируемой в точке (x, y, z,...) , если ее

приращение допускает выделение главной линейной части

∆u =∆f (x, y, z,...) = f (x +∆x, y +∆y, z +∆z,...) − f (x, y, z,...) =

= A∆x + B∆y +C∆z +...+o(	∆x2 +∆y2 +∆z2 +...),
называемой дифференциалом функции	dy ≡ ∆y, dz ≡ ∆z,...).
du = df (x, y, z,...) = Adx + Bdy +Cdz +... (dx ≡ ∆x,

Если дифференциал du , то частные производные ux′, u′y , uz′,..., причем

du =u′xdx +u′ydy +u′zdz +...

Правила дифференцирования функций нескольких переменных, связанные с арифметическими операциями, полностью аналогичны соответствующим правилам для функций одной переменной:

Теорема (правила дифференцирования). Пусть

1) u = f (x,...), v =

1)(u +v)′x =ux′ +vx′

2)(u −v)′x =ux′ −vx′

3)(uv)′x =ux′v +uvx′

4)(uv )′x =ux′vv−2uvx′

g(x,...)
…	d (u +
…	d (u −
…	d (uv)
…	d (uv )

v) =du +dv v) =du −dv

=du v +u dv

=du v −u dv

v2

Решения.

№ 26.1.

x

′

z′x =

(

)

=

1

z = x

y

y

x

y

(y )

y

y2

z′y =

x

′ =(x y−1 )′

=x (−y−2 )=−

x

y

Сравнить.

z =

x

dz =d

x

=

dx y −x dy

=

1

dx −

x

dy

y

y

y2

y

y2

z′

=

1

y

x

dz =

1

dx −

x

dy

x

y

y2

z′

=−

y2

y

z′

=

1

x

y

x

z′

=−

y2

y

№ 26.3.			(x2 3 y )
z=arctg
z′x =(arctg (x2 3 y ))′											=					1									(x2 3				y )′		=				1								2x 3			y
													1+(x2 3 y )									2																	2
										x																				x	1+(x2 3 y )
																																																′
					2		3		′								1										2 3		′						1									2			1										1							2	1		−	2
																																															3																					3
z′y =(arctg (x								y ))		y =					(	2					)	2			(x				y )	y	=		(		2			)		2			(x		y			)y =						(			2				)	2	x		(3 y				)
																		3		y														x 3 y																						x		3	y
													1+ x																				1+																		1+
																																			1										1										1											2
																													dz=												2x y3 dx+																				x2 (13 y−					3 )dy
																																					1		2																			1		2
																															1+(x2 y3 )																		1+(x2 y									3 )
Сравнить.
				1								1																1
d arctg (x2 y				3 )=															d (x2 y									3 )=																1												1
								1+(x							1		2																	z′x			=															2x y3
												2																										1+(x2 y										1	2
														y3 )																																		3 )
																										)																		1											(	1 y			−	2	)
													1										−2											z′			=															x2
		1													+ x2					1 y																																								3
=						2xdx y							3										3					dy								y		1+(x2 y										1	2							3
1+(x		2	1	2															(3																													3 )
			y3 )

№ 26.5.

z′

=(x

y

′

α

′

α−1

= yx

y−1

)

x

= (x

)

=α x

x

dz = yxy−1dx +xy ln xdy

z =xy

′

′

z′

=(x

y

y

=a

y

=x

y

ln x

)

y

= (a

)

ln a

y

Сравнить.

(

dy ln x+y 1 dx

)

y−1

z=xy dxy =dey ln x =ey ln xd( y ln x)=xy

= yxy−1dx+xy ln xdy

z′x =yx

x

z′y =xy ln x

Замечание.

Нахождение дифференциала df функции нескольких переменных f (x,...)

полностью аналогично случаю функции одной переменной f (x) . В то же время,

при

нахождении частных производных приходится “переключать” сознание с одной переменной на другую, воспринимая функцию нескольких переменных последовательно, как функцию одной какой-либо переменной, считая остальные – постоянными параметрами. В этом смысле – порой “проще” найти дифференциал и из него получить частные производные.

№ 26.6.

y

u =x z

du =dx z

=de z ln x =e z ln xd (zy

ln x)=x z

(d zy

ln x + zy d ln x)=

y

y

y

y

y

dy z − y dz

y

1

y

y

1

y

z

z

=x

z2

ln x +

z

x

dx

=x

dx +

z

ln xdy −

z2

ln xdz

=

xz

y

z

−1

1

z

y

z

y

y

y

=

x

dx +

x

ln xdy −

x

ln xdz

z

z

z2

№ 26.8. u=xyz

du=dxyz =deyz ln x =eyz ln xd (yz ln x)=xyz (dyz ln x+yzd ln x)=

=xyz (dez ln y ln x+yz 1x dx)=xyz (ez ln y (dz ln y+z 1y dy)ln x+yz 1x dx)= =xyz −1 yzdx+xyz yz−1z ln xdy+xyz yz ln y ln xdz

y

y

−1

u′

=

x z

z

x

1

y

z

u′y = z x

ln x

u′

=−

y

x

y

ln x

z

2

z

z

u′x =xyz −1 yz

u′y =xyz yz−1z ln xu′z =xyz yz ln y ln x

№ 26.9.

1,11,8 =?

Рассмотрим	функцию	двух переменных z = f (x, y) = xy . Требуется ее вычислить
приближенно, при:
x =1,1=1,0 +0,1= x0 +∆x,		x0 =1,	∆x =0,1
y =1,8 =2 −	0, 2 = y +∆y,	y =2,	∆y =−0, 2
	0	0

Из определения дифференциала
∆f (x0 , y0 ) =df (x0 , y0 ) +o( ∆x2 +∆y2	)	≈ df (x0 , y0 ) = fx′(x0 , y0 )∆x + fy′(x0 , y0 )∆y
		∆x, ∆y≈0

вытекает

f (x0 +∆x, y0 +∆y) − f (x0 , y0 ) ≈ fx′(x0 , y0 )∆x + fy′(x0 , y0 )∆y ,

или

f (x, y) ≈ f (x0 , y0 ) + fx′(x0 , y0 )(x − x0 ) + fy′(x0 , y0 )( y − y0 )

Имеем (см. № 26.5.)

z =xy dxy =dey ln x =ey ln x d( y ln x) =xy (dy ln x + y 1x dx)= yxy−1dx + xy ln xdy xy ≈x0y0 + y0 x0y0 −1 (x −x0 )+ x0y0 ln x0 (y − y0 )

1,11,98 ≈1,02,0 +2,0 1,02,0−1 0,1+1,02,0 ln1,0 (−0, 2)=12 +2 11 0,1−12 ln1 0, 2=1+2 0,1−0, 2 0=1, 2

Сравнить с “точным” значением

1,1871533798287798424543353896876 …

Замечание. По-существу, при приближенном вычислении функции, мы воспользовались формулой Тейлора с точностью до слагаемых первого порядка малости:

f (x, y) = f (x0 , y0 ) +df (x0 , y0 ) +o ( ∆x2 +∆y2 )1 ≈ f (x0 , y0 ) +df (x0 , y0 )

№ 26.10.

Имеем:

	p =2(x+ y),	S =x y sinα .
При изменении сторон	x →x+∆x =x+dx,	y → y+∆y = y+dy	и угла между ними
α →α +∆α =α +dα периметр p и площадь S изменятся приблизительно на
∆p ≈dp =d (2x+2 y)=2dx+2dy ;
∆S ≈dS =d (xy sinα )= y sinαdx+x sinαdy+xy cosαdα.
№:26.11.
Имеем:
S =SOCH =πr2 ,	C =SδOK =πr r2 +h2 , V =VKOH =1 h SOCH =1 h πr2 .
		3	3

При изменении радиуса основания r →r +∆r =r +dr и высоты h→h+∆h=h+dh

площади

основания S , боковой поверхности C и объем конуса V изменятся приблизительно на

∆S ≈dS =d(πr2 ) =2πrdr ;

∆C ≈dC=d (πr

r2 +h2 )=πdr r2 +h2 +πr

1

(rdr +hdh)=π

2r2 +h2

dr +π

rh

dh

r2 +h2

r2 +h2

r2 +h2

1

2

1

1

2

∆V ≈dV =d (3πr

h)= 3 2πrhdr +

3πr

dh

27. Производная по направлению. Градиент

Условия.

№ 27.1. Высота поверхности над данной точкой местности (x, y) равна: z = f (x, y) . Найти:

1)крутизну подъема поверхности в точке A(xA , yA ) в направлении точки B(xB , yB ) ;

2)величину и направление наибольшего роста (убывания) высоты в точке A(xA , yA ) ;

3)скорость изменения высоты вдоль линии уровня.

z = x2 + y2 ,				A(1, 2) →B(4, −2)	z = x2 + y2 ,	A(2,1) →B(6, −2)
№ 27.2. Температуранеравномернонагретой					пластинывточке (x, y)		равна: u = f (x, y) .
Найти:
1)	скорость изменения температуры в точке A(xA , yA ) в направлении точки B(xB , yB ) ;
2)	величинуинаправлениенаибольшегороста(убывания) температурывточке A(xA , yA ) ;
3)	скорость изменения температуры вдоль изотермы.
		x				π	π
u =sin			,	A(π, −1) →O(0,0)	u =cos (xy2 ),	A(2	, −1)→B(32 ,0)
		y

№ 27.3. Потенциал электростатического поля, созданного неравномерно распределенным в некотором объеме зарядом, вточкепространства (x, y, z) равен:

u = f (x, y, z) . Найти:

1)скоростьизмененияпотенциалавточке A(xA , yA , zA ) внаправленииточки B(xB , yB , zB ) ;

2)величинуинаправлениенаибольшегороста(убывания) потенциалавточке A(xA , yA , zA ) ;

3)скорость изменения потенциала вдоль эквипотенциальной поверхности.

u =xy2 −z3, A(2,3,4) →B(4,−3,7)

u =x3 y2 − z , A(1, −2,4) →B(3,1, −2)

№ 27.4. Найти величину и направление градиента функции.

u =−γ

M

=−γ

M

u = k

r

2 = k (x2

+ y2

+ z2 )

r

x2 + y2 + z2

2

2

Теория.

Удобно рассматривать функцию нескольких переменных z = f (x, y) , как функцию

векторного аргумента z = f (r ) :

r = x .y

Придадим	приращение		∆r = ∆t e	радиус-
вектору r точки (x, y) величины ∆t по
направлению единичного вектора e = ex .
			e
				y
Производной функции z = f (r ) в точке r по
направлению e называется							f (x +∆t ex , y +∆t ey ) − f (x, y)
z′	(r ) = ∂f	(r ) = lim	f (r +∆te) − f (r )		= lim			.
e	∂e	∆t→0	∆t		∆t	→0	∆t

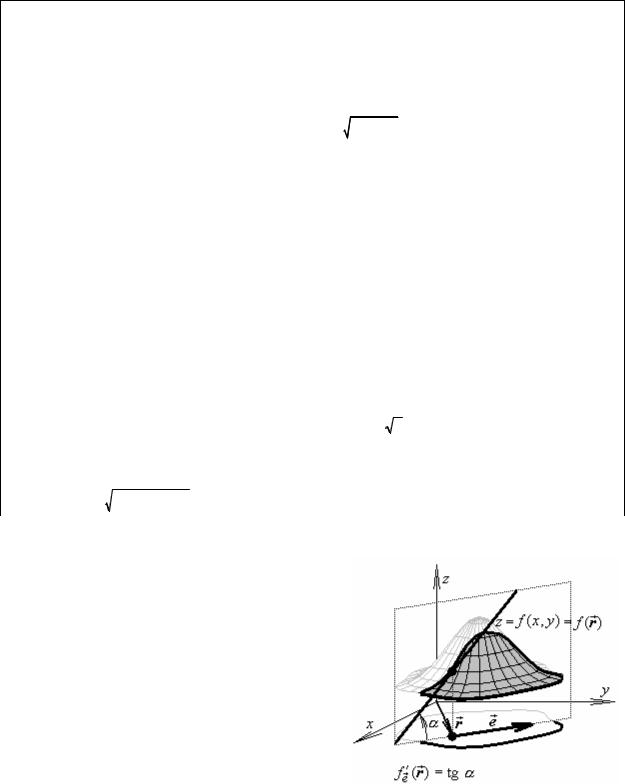
Геометрический смысл производной по направлению (в случае функции двух переменных) – тангенс угла между касательной прямой к сечению поверхности z = f (r ) ,

вертикальной плоскостью, параллельной направлению e , и координатной плоскостью xOy : fe′(r ) = tg α (крутизна подъема поверхности в точке r по направлению e )

Физический смысл – скорость изменения функции в точке r по направлению e .

Если функция дифференцируема, то:
			z′
	ze′ (r ) = zx′ ex + z′y	ey =(grad z, e)
			, где grad z = z′x
			y

вектор градиента функции. Из геометрического и физического смысла производной по направлению вытекает геометрический и физический смысл градиента:

Теорема.

1)	направление grad f (r ) – направление emax наибольшего роста функции u = f (r ) ;
2)	длина grad f (r ) – величина ue′max наибольшего роста функции u = f (r ) ;
3)	grad f (r ) поверхности(линии) уровня u = f (r ) = const , проходящейчерезточку r .

grad u=emax ue′max .

Решения.

№ 27.1.

подъема поверхности z = x2 + y2 в

A(1,2) в направлении точки

1)

Крутизна

точке

B(4,−2) - это

производная функции z = x2 + y2

в точке A(1,2) по направлению

e ↑↑ AB :

ze′ (r ) =(grad z, e) = zx′

ex + z′y

ey .

Имеем:

zx′

=2x

(1,2) =2

2

grad z =

z′

=2 y

=

4

4

y

(1,2)

Далее

4 −1

3

AB =

=

−2 −

2

−4

AB

= 32 +(−4)2 =5

3

e =

AB

5

=

4

AB

−

5

Наконец

z′ (1, 2) =2 3 −4

4 =−2.

e

5

5

2) Величина и направление наибольшего роста (убывания) высоты в точке A(1,2) – это величина и направление вектора градиента (антиградиента)

2

2

grad z

20

grad z =

ze′

=

grad z

= 22 +42 =

20

, emax =

=

4

4

max

grad z

20

3)

Скорость изменения высоты вдоль линии уровня

z(x, y) =const =z(1,2)

x2 + y2 =5,

очевидно, равна нулю.

Замечание.

Линия уровня x2 + y2 =5 – это окружность с центром в начале координат.

Радиус-вектор r точки A(1,2) одновременно радиус

этой

окружности,

а

значит ,ей

ортогонален. Остается обратить внимание,

что grad z =2r ,

т.е.

grad f (r ) линии уровня,

проходящей через точку r .

№ 27.2.

x

1)

Скорость изменения температуры u =sin

в точке

A(π,−1)

по направлению точки

y

O(0,0) – это производная функции u =sin

x

в точке A(π,−1)

по направлению

e ↑↑ AO :

y

Имеем:

u′

=cos

x

1

=−cos (−π )=1

x

y y

(π ,−1)

1

grad u =

x

x

π

u′

=cos

−

=−cos (−π )π =π

2

y

y

y

(π ,−1)

Далее

0 −π

−π

= (−π )2 +12

= π 2 +1 e =

AO

1

−π

AO =

=

AO

=

(

)

AO

π 2 +1

0 −

−1

1

1

Наконец

1

(

)

ue′ (π, −1) =

(

)

=0.

π 2 +

1

1 −π

+π 1

2)

Величина

и

направление

наибольшего

роста (убывания)

температуры

в точке

A(π,−1)

– это величина и направление вектора градиента (антиградиента)

1

= 1+π 2

e

grad u

1

1

grad u =

u′

=

grad u

,

max

=

=

π

e

grad u

1+π 2

π

max

Замечание. Направление антиградиента emin =−emax поля температур – это направление

потока тепла в данной точке, которое распространяется из мест с более высокой температурой в места с более низкой, т.е. в направлении наибольшего убывания температуры.

3) Скорость изменения температуры вдоль изотермы (линии уровня)

	u =sin	x	=const =u(π,1)	sin	x	=0	x	=π ,
		y			y		y

очевидно, равна нулю.

Замечание. Данное в примере направление e – это направление вдоль изотермы.